基于相关系数稀疏表征的转子振动信号周期特征提取

唐振宇，黄凯，杨期江，朱晓彬

(广州航海学院船舶与海洋工程学院，广东广州 510725)

0 前言

在旋转机械转子系统的运行过程中，因受到测试环境、测试仪器和人为因素等影响，传感器所采集的振动信号易被噪声污染，且旋转机械结构复杂，振动信号往往由多个部件的振动叠加而成。转子振动信号具有非高斯、非平稳的特性。传统的信号处理方法对含有噪声的混叠信号进行分析时有明显不足，这也对机械的状态监测和故障诊断带来了巨大的困难。

传统的信号处理方法如小波分解、经验模态分解(Empirical Mode Decomposition,EMD)已被广泛应用于旋转机械振动信号分析，但对于含噪的混叠信号，上述方法仍存在明显不足。小波分解在对转子振动信号分析时存在以下问题:(1)小波分解层数的确定需要信号的频率结构和采样频率等先验知识;(2)小波基和阈值的选择困难。经验模态分解也存在模态混叠和端点效应问题，导致基于EMD的方法效果不佳。改进的EMD方法如集合经验模态分解(EEMD)是将噪声辅助分析加在经验模态分解中，有效地抑制了模态混叠的现象，但无法完全消除混叠现象。因此对于信号的分解，应该根据信号本身的结构特点，自适应选择基函数完成信号的分解。1993年MALLAT和ZHANG提出了基于过完备字典对信号进行稀疏分解的思想，同时也提出了匹配追踪算法。2004年有学者建立了压缩感知理论(Compressing Sensing，CS)。压缩感知理论证明了信号在某个变换空间内具有稀疏性，可仅用少量数据保留信号的大部分特征，这样可以用远低于奈奎斯特采样定理要求的采样频率完成信号的重建恢复，这也将稀疏分解带到了一个新高度。稀疏分解存在稀疏度过大，重构信号的噪声分量增加，而稀疏度过小，重构信号又会丢失重要特征信息的问题。其中，稀疏度为信号中非零元素的个数。针对稀疏度选取问题的研究，文献[6]提出了稀疏度自适应匹配追踪算法(Sparsity Adaptive Matching Pursuit,SAMP)，文献[7]提出变步长自适应匹配追踪算法，文献[8]提出基于CS的稀疏度变步长自适应压缩采样匹配追踪算法。

对于稀疏度的研究，国内学者大多是对SAMP算法进行改进。本文作者提出互相关稀疏分解的方法，将互相关函数引入稀疏分解中以凸显稀疏分解后各分量与原信号之间的相关性，并计算相关系数以解决稀疏度的选取问题。采用所提方法进行仿真实验和转子振动信号实例分析，成功提取振动信号周期特征。

1 互相关稀疏分解原理

1.1 信号的压缩感知

以转子系统为核心部件的旋转机械运行工况复杂，传感器采集到的信号含有大量噪声。转子振动信号数学模型为

()=()+()

(1)

式中：()为转子振动信号；()为噪声。对于实信号()，如果它在稀疏字典中是稀疏的，则用观测矩阵对信号进行压缩传感，得到观测信号。压缩传感方程表示为

=

(2)

有效的压缩传感要求观测矩阵与稀疏字典互不相关，否则无法求解。高斯矩阵是压缩传感常用的测量矩阵，满足RIP性质。

1.2 稀疏分解理论

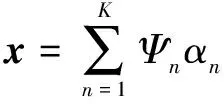
(3)

其中:为每个字典原子相对于原信号的权重，集合为稀疏系数，且只有个非零值。

1.3 正交匹配追踪算法

常见的自然信号在时域是不稀疏的，信号稀疏分解理论指出，信号可以经过变换矩阵进行稀疏表示。由式(2)可以看作原信号在观测矩阵下的线性投影，显然的维数远低于的维数，用进行稀疏分解更为容易。结合式(2)(3)得出下式:

=α

(4)

式中:=为×的矩阵(≪)，称为感知矩阵。此时满足约束等距条件，可以通过求解式(5)的最优化范数式重构信号。

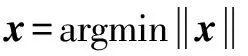
s.t.=

(5)

式(5)本质上是一个优化问题，即NP-hard问题。本文作者利用正交匹配追踪算法(Orthogonal Matching Pursuit，OMP)选取多个字典原子计算信号最优逼近，使得误差最小。OMP通过求残差与感知矩阵中各个原子之间内积值的绝对值，来计算稀疏系数。内积的绝对值越大说明感知矩阵中的这一列原子与信号越相关。

={|=|〈,〉|,=1,2,…,}

(6)

并采用最小二乘法对信号进行逼近和残差更新：

(7)

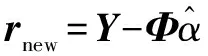
(8)

OMP算法具体步骤如下:

(1)初始残差=，迭代次数=1，索引值集合=、=;

(2)计算残差与感知矩阵中各个原子之间内积值的绝对值，并将中的最大值对应的索引值存入中;

(3)更新感知矩阵，其中=∪;

(4)应用公式(7)得到，同时用式(8)对残差进行更新;

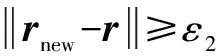
1.4 过完备字典构造

过完备字典是一组具有广泛时频特性的函数波形,每个波形作为字典中的一列，这一列称为原子，原子的数量是冗余的。基于过完备字典的稀疏分解能够根据信号的结构特征提取信号的各种局部特征，实现信号的自适应分解，获得信号的稀疏表示。

针对转子振动信号的周期特征，构造离散傅里叶变换矩阵(Discrete Fourier Transform,DFT)，长度为的转子振动信号()通过DFT矩阵变换后转化为()的形式:

(9)

即=，上述过程表示为矩阵形式为式(10)

(10)

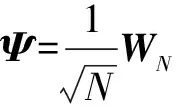
(11)

公式(11)将其归一化后可得到过完备字典。

1.5 皮尔逊相关系数

皮尔逊相关系数是用于度量2个向量之间线性相关性的变量，计算公式为

(12)

其中:为信号的点数;为[-1 1]之间的数，越接近于1，则2个变量之间的相关性越高。

采用皮尔逊系数作为稀疏分解效果的评判标准。计算稀疏分解后的信号与原信号的相关性。一般情况下，当>0.7时，认为稀疏分解的信号与原信号相关性好，是真实的分量，予以保留。

2 仿真实验及分析

转子振动信号波形复杂，由其转频及倍频和随机噪声等组成。依据上述特点，构造仿真信号()，设置采样频率=2 000 Hz，采样点数=1 200,则有：

()=sin(2π)+sin(2π)+sin(2π)+()+()

(13)

()=e-sin(2π)

(14)

其中：为转子转频;、分别为2倍频和3倍频;()为转子正常运行时产生的冲击衰减分量;()为均值为0且方差为1的高斯白噪声。

设幅值=2 mm、=1.6 mm、=1.2 mm、=0.2 mm、=50 mm;基频=30 Hz; 倍频、分别为60、90 Hz;冲击频率=50 Hz。仿真信号()的时域波形如图1所示，频谱如图2所示。

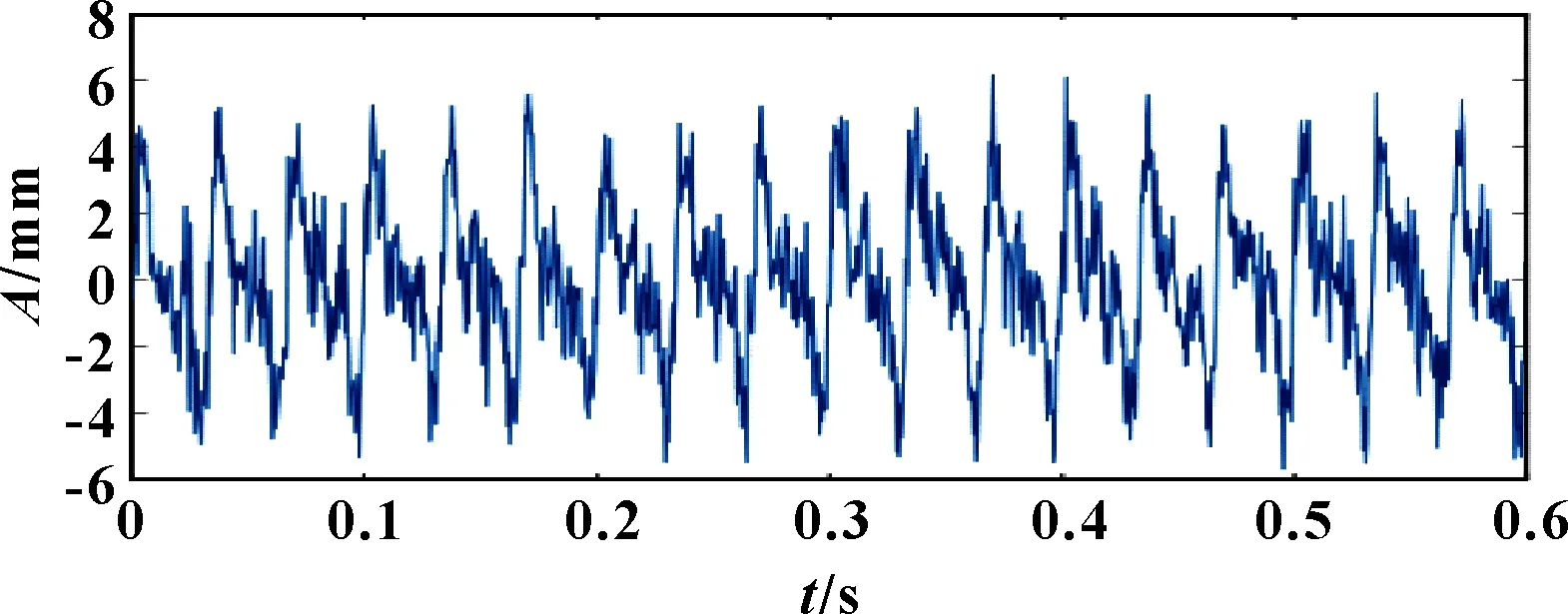
图1 仿真信号X(t)的时域波形

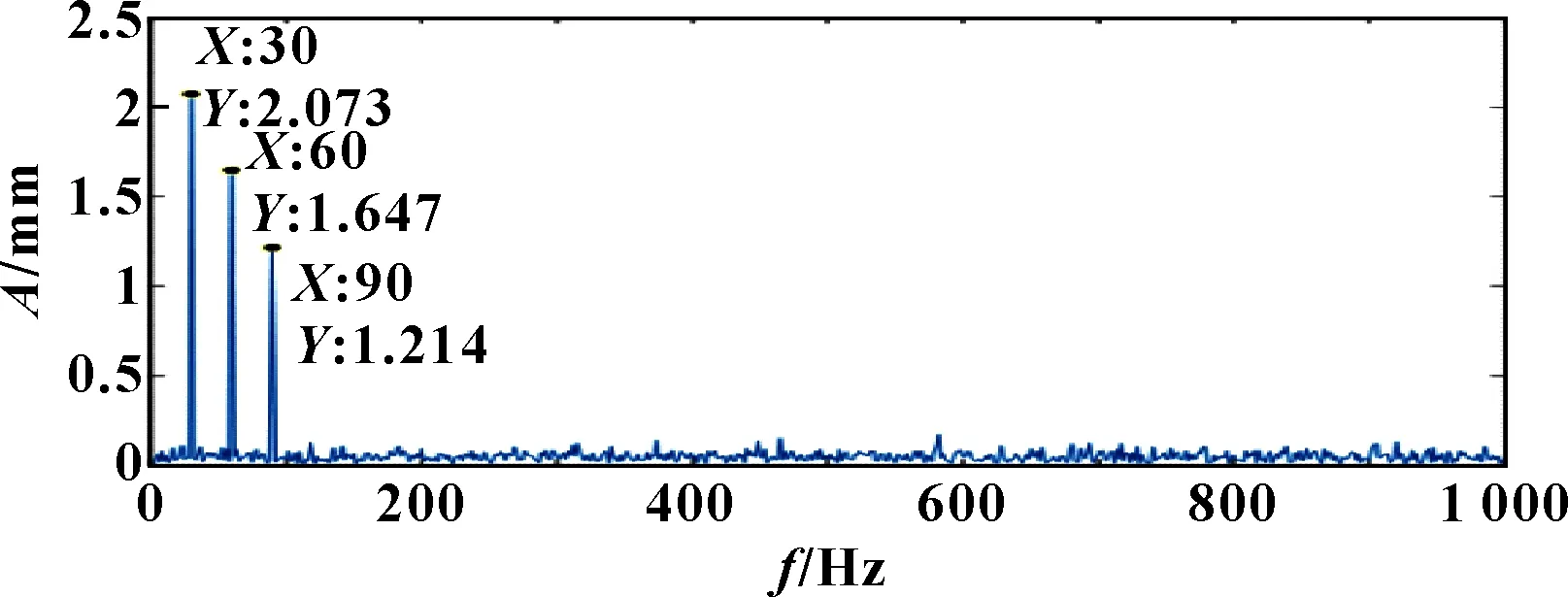
图2 仿真信号X(t)的频谱

构造大小为516×1 200的高斯观测矩阵，对仿真信号进行降维处理，经式(2)得到大小为1×516的观测信号。再构造大小为1 200×1 200的离散傅里叶变换字典与观测矩阵相乘得到感知矩阵。基于感知矩阵，采用正交匹配追踪算法对观测信号()进行重构，得到稀疏系数的集合。根据式(12)分别计算出不同稀疏度时，重构信号()与仿真信号()的皮尔逊相关系数如表1所示。仿真信号()由3个主要分量组成，稀疏度取值应大于3。稀疏度越大，重构信号与仿真信号的相关性越强，当值大到一定程度时，相关性并无明显提高，甚至会混入噪声。根据实验结果并考虑时效性，重构信号的稀疏度选取为6。=6时，重构信号()如图3所示，其频谱如图4所示。

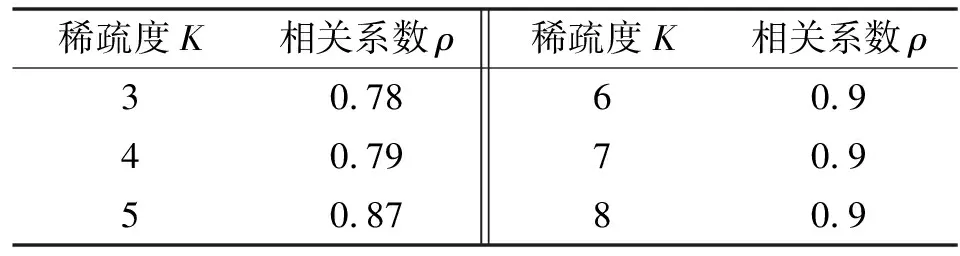
表1 稀疏度K

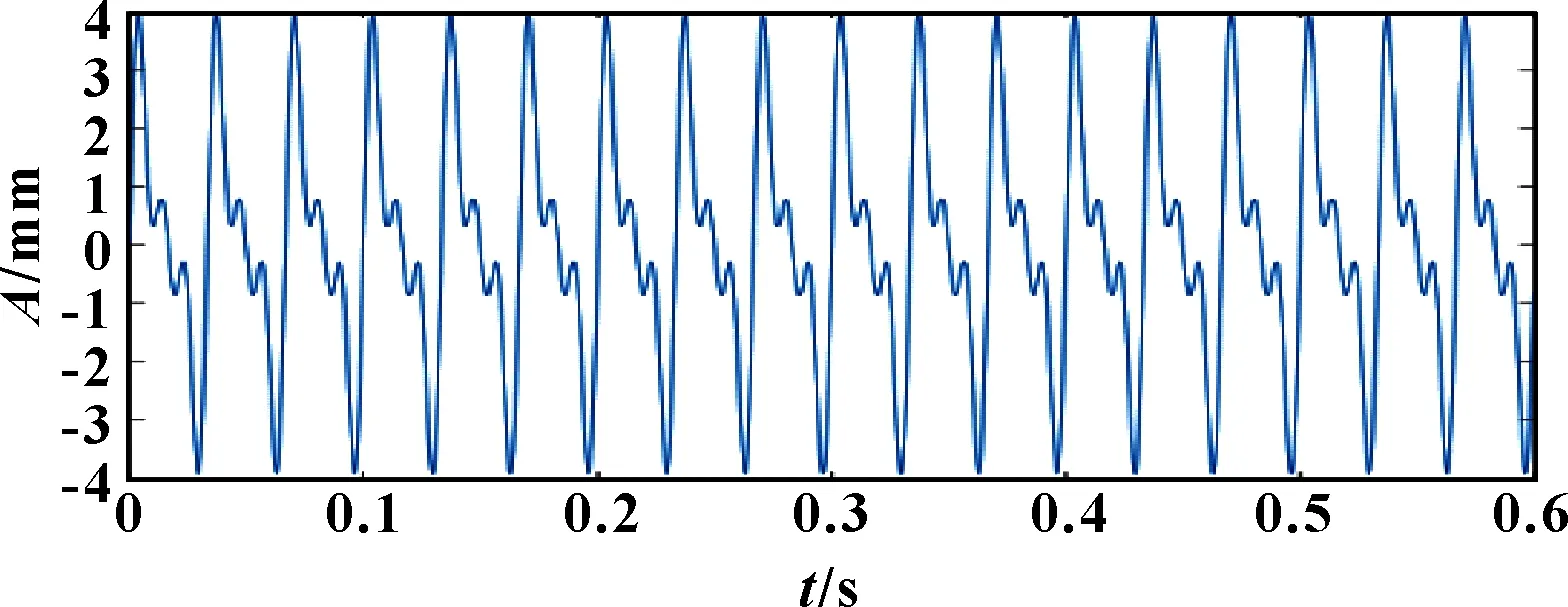
图3 重构信号Sc(t)

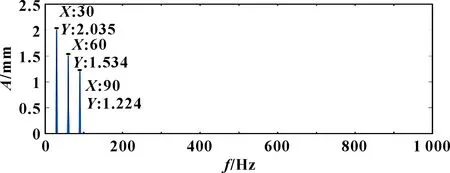
图4 重构信号Sc(t)频谱

由图3、图4可知：原始信号经重构后，噪声和冲击分量得到了有效抑制且重构信号保留了原始信号的大部分特征，谱峰与原始信号的谱峰误差精确到0.01 Hz。现将稀疏系数中不为零的项与感知矩阵对应原子相乘，分离仿真信号不同的频率成分。稀疏度=6时，稀疏分解结果如图5—图7所示。经MATLAB仿真计算，分离出的()～()与仿真信号()对应的转频、倍频成分相关性均达到0.99。

图5 稀疏分解信号Sc0(t)

图6 稀疏分解信号Sc1(t)

图7 稀疏分解信号Sc2(t)

3 转子振动信号分析

3.1 轴承转子实验台

实验对象为Bently小型轴承转子实验台，该实验台主要由驱动系统、控制系统、采集系统及机械结构等部分组成。为降低外界振动对轴承转子系统的影响，在实验平台与轴承转子系统之间增加具有良好减振性能的减振支座，最大程度地隔绝外界因素对实验台的干扰。Bently小型轴承转子实验台如图8所示，其中振动采集系统为LMS多功能数据采集器。

图8 转子实验台实物图

3.2 转频和倍频信号提取

使用LMS数据采集系统采集振动加速度信号，采样频率为16 384 Hz，转速为4 000 r/min。其时域波形、频谱及时频图分别如图9—图11所示。在4 000 r/min工况下，信号D1的转频为65.6 Hz，频谱内存在高频噪声和转子系统运行时激发的谐波分量。

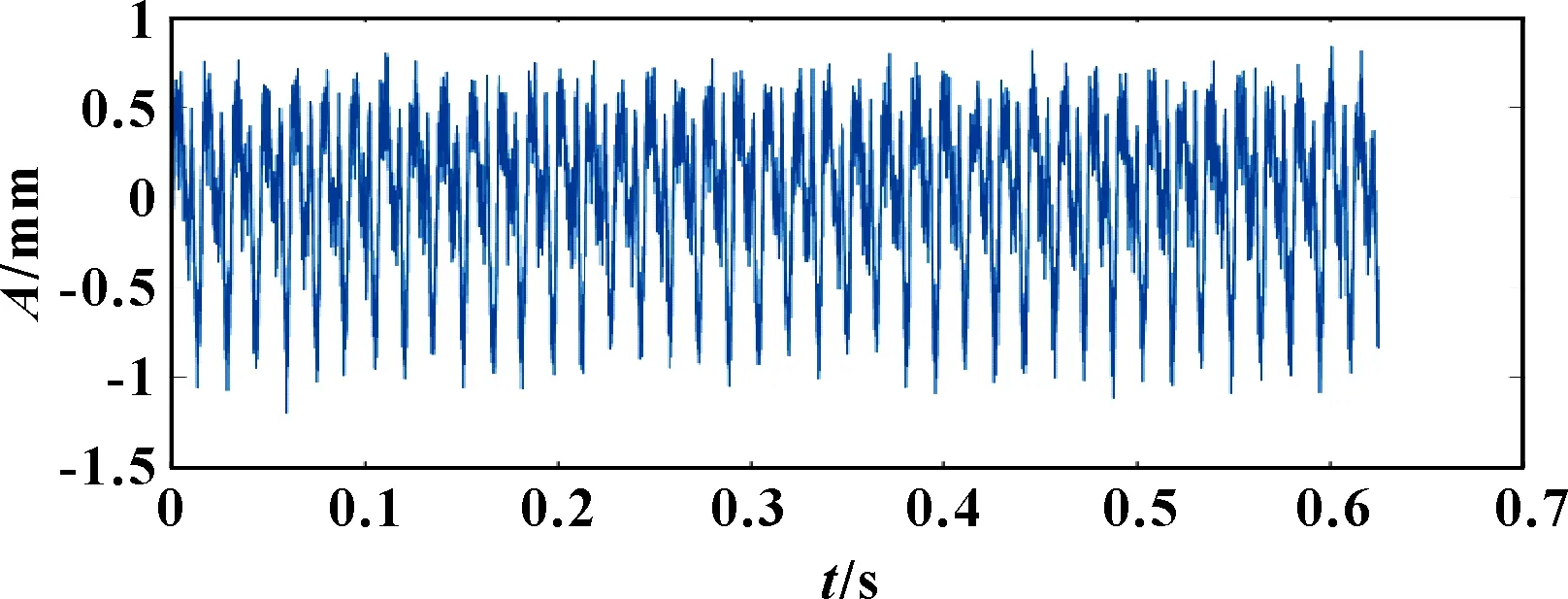
图9 转子振动信号D1时域波形

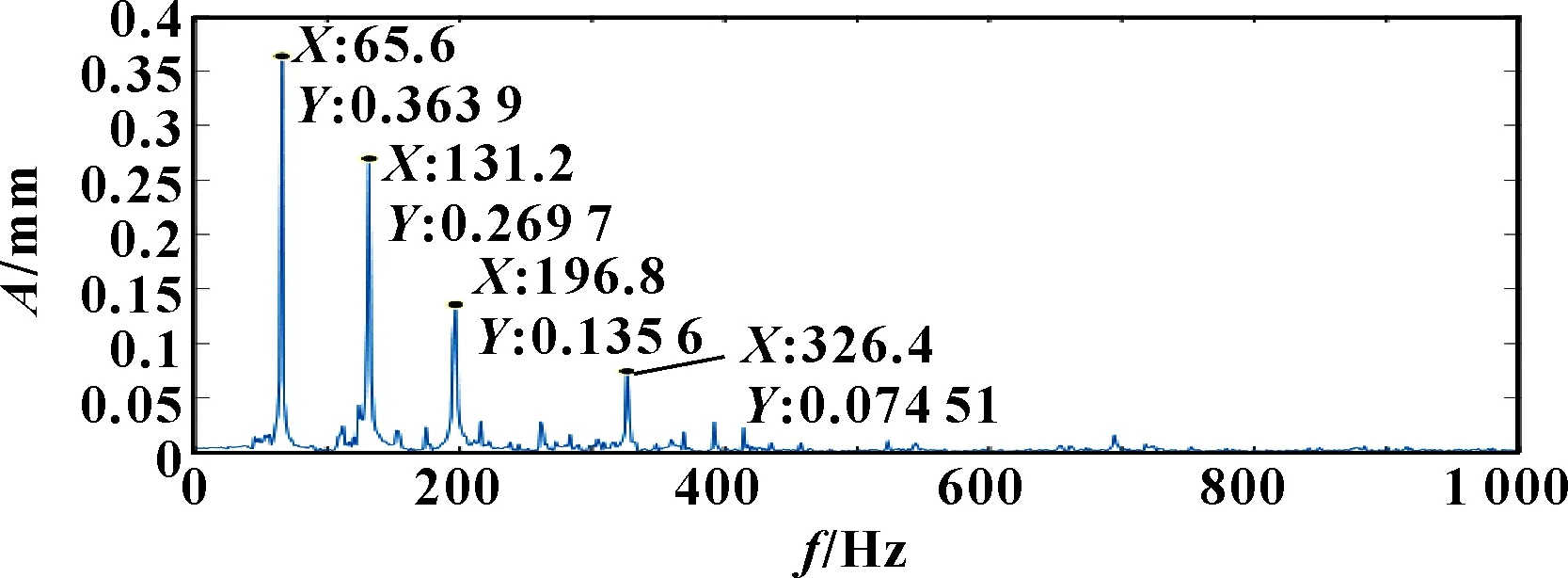
图10 转子振动信号D1频谱

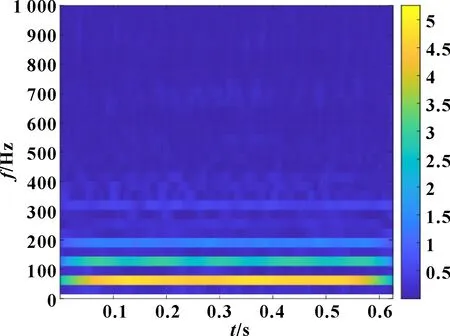
图11 转子振动信号D1小波时频图

由图10可知：可以提取4个分量，分别为(65.6 Hz,0.363 9 mm)、(131.2 Hz,0.269 7 mm)、(196.8 Hz,0.135 6 mm)、(326.4 Hz,0.074 51 mm)，滤除其余无用成分。

经MATLAB计算，当稀疏度=16时，重构信号与信号D1的相关系数为0.9，接近于1，相关性高。文中取=16对信号进行稀疏分解，结果如图12—图15所示。可以看出：文中方法准确地提取了转子振动信号的转频及倍频成分。

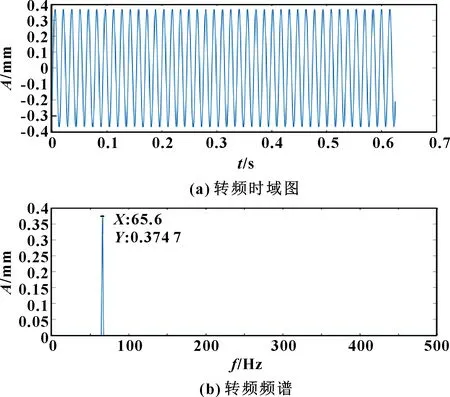
图12 转子转频

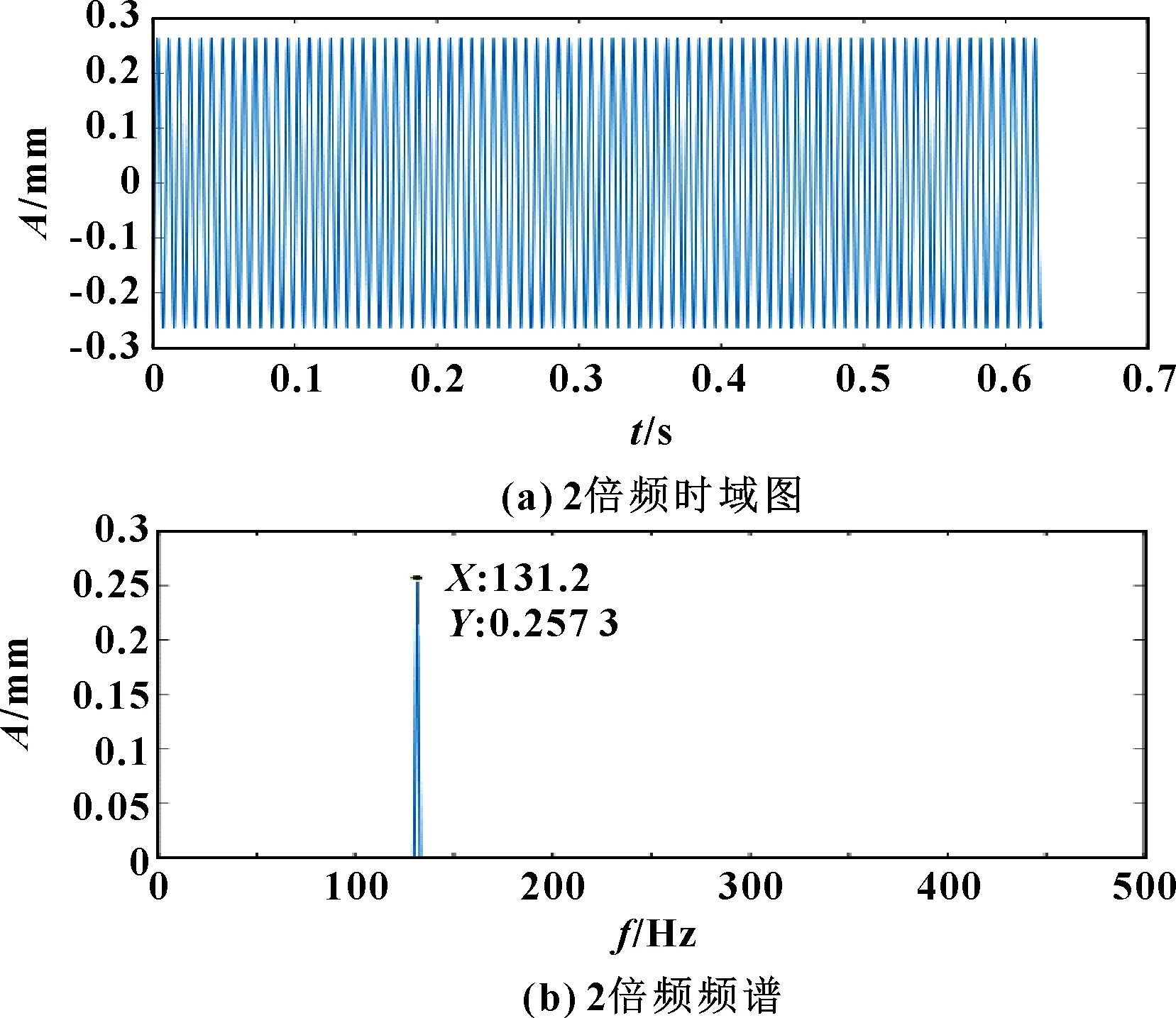
图13 转子2倍频

图14 转子3倍频

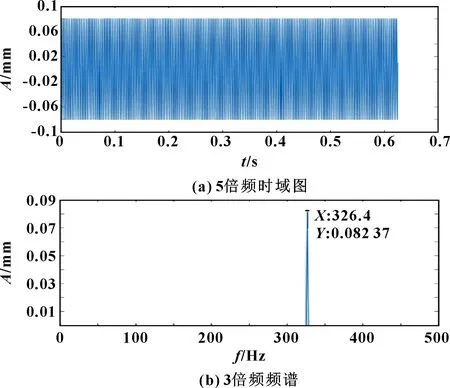
图15 转子5倍频

以上实际工程应用证明文中方法的有效性和可行性，为转子运行状况监测和故障诊断提供纯净的信号，有利于进一步信号分析。

4 结论

为解决传统信号处理方法难以对含噪混叠信号进行分析的难点，本文作者提出互相关稀疏分解法。利用该方法对信号采用压缩感知，仅需少量数据就可以保留信号的大部分特征，用远低于奈奎斯特采样定理要求的采样频率完成信号的重建恢复，进而引出稀疏度对重构信号的影响。稀疏度过大，重构信号的噪声分量会增加，过小，重构信号会丢失特征信息。因此，需选择最合适的稀疏度完成对仿真信号的降噪重构。

为了验证该方法的可行性，首先利用皮尔逊系数计算稀疏分解后的信号与原信号的相关性，并通过计算相关系数来解决稀疏度的取值问题。当稀疏分解的信号与原信号相关性好(>0.7)时，保留该信号。将稀疏系数与字典中对应的原子相乘，分离出仿真信号中不同的频率成分，最后对转子振动信号实例进行分析，成功提取转子的转频及其倍频成分。仿真实验结果验证了该方法的有效性和可行性，可为转子运行状况监测和故障诊断提供纯净的信号，有利于进一步分析信号。结果表明：与传统的信号处理方法相比，用互相关稀疏分解法处理的旋转机械运行的含噪混叠信号更易于分析，有助于旋转机械的运行状况监测和故障诊断。