中心差商公式变步长算法的计算终止条件

令锋

（肇庆学院数学与统计学院，广东 肇庆 526061）

1 问题的提出

数值微分是指将函数y=f(x)在给定点a的导数用点a附近节点上函数值的线性组合近似表示[1-2].科学研究与工程技术领域中的许多问题都需要计算函数f(x)在给定点的导数，当f(x)表达式复杂或函数仅由表格给出时，就需要进行数值微分，中心差商公式是数值微分采用的一种重要算法.

记h为步长，f(x)在节点a-h，a及a+h处的函数值分别为f(a-h)，f(a)和f(a+h)，则求f(x)在点a处一阶导数的中点公式及截断误差分别为

求函数f(x)在点a处二阶导数的三点公式及截断误差分别为

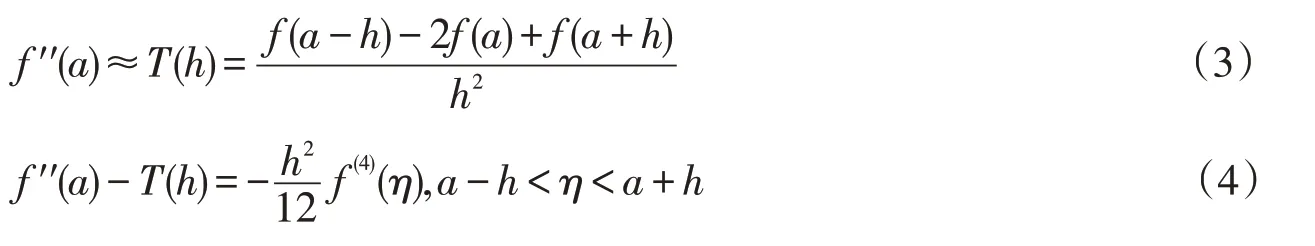
对公式（1），从截断误差角度分析，h越小计算结果越准确；但从舍入误差或计算稳定性角度考虑，h越小，f(a-h)与f(a+h)的值将越接近，两个相近数相减会导致有效位数严重损失，因而用中心差商公式（1）计算一阶导数时步长不宜太小或太大，存在最优步长，当h取值小于最优步长后，计算误差反而会增大[2-4].同理，采用公式（3）计算二阶导数时也存在最优步长.

中心差商公式（1）及（3）都具有二阶计算精度，且公式简单，编程方便，是数值微分值得采用的方法.但由于步长很小时计算结果对步长变化敏感，大多数教材没有进一步讨论两点公式与三点公式的计算机实现，个别教材中虽然提出宜采用变步长方法计算，但没有给出详细的分析、说明和示例，尤其是没有给出计算终止条件[5]，因而编程实现算法存在困难.本文通过分析确定中心差商公式中最优步长面临的问题，提出以计算结果满足精度要求作为计算终止条件和以步长最接近最优步长作为计算终止条件两种算法，以期能够采用中心差商公式的变步长算法求得函数在给定点具有较高精度的一阶及二阶导数.

2 中心差商公式最优步长的确定

设f(a)，f(a-h)和f(a+h)的舍入误差分别为ε0，ε1和ε2，ε=max{|ε0|,|ε1|,|ε2|}，则计算f′(a)与f′′(a)的舍入误差分别为

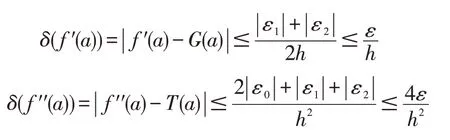
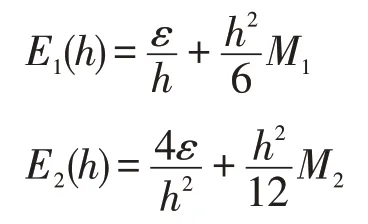
根据求极值的方法，要使误差 取最小值，h应满足

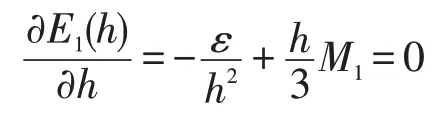
同理可得，使误差E2(h)达到最小值的最优步长为

求出M1与M2的工作较繁琐，在某些情形下甚至无法实现，从而确定最优步长面临诸多困难.为获得具有较高精确度的计算结果，通常采用中心差商公式变步长算法.以计算一阶导数为例，首先选择一个初始步长h0，为方便计算，通常取h0=1，利用公式（1）求出G(h0)，然后将步长减半得h1，再计算G(h1)，如此反复，使步长在逐步减半的过程中逐步接近最优步长，从而获得精度较高的计算结果.因而，在变步长中心差商微分法的计算机实现过程中，确定正确的计算终止条件是算法得以实现的前提.

3 中心差商公式变步长算法的计算终止条件

设对初始步长h0经n次减半后得到的步长为h0，函数y=f(x)在点a相应的导数f′(a)及f″(a)的近似值分别为G(hn)和T(hn)，以下给出两种计算终止条件.

3.1 满足精度要求时终止计算

如果给定了计算精度要求ε，则前后两次步长减半得到的导数近似值应满足如下条件

此即给定精度要求时变步长数值微分法的计算终止条件.

上述算法容易编程实现且避免了直接计算最优步长，可望获得理想的计算结果.但由于步长过小时误差反而会更大，当要求的精度很高时，通过将步长逐步减半的方法可能无法获得满足精度要求的计算结果.实际计算时，为避免舍入误差不断增大出现较大误差数值错误结果，可预设一个步长最大减半次数M，当步长减半次数超过最大减半次数时停止计算.

若以计算结果满足精度要求作为计算终止条件，用三点公式（3）计算函数f(x)在点a的二阶导数算法可描述如下：

算法1：数值微分的变步长三点公式算法

1） 输入函数f(x)以及点a的值.

2）输入计算精度要求ε及步长最大减半次数M.

3） 步长减半次数n=0,h=2-n=1，计算T0(f(a-h)-2f(a)+f(a+h))∕(h2).

3） 步长减半：n=1,h=2-n=1∕2，计算T1(f(a-h)-2f(a)+f(a+h))∕(h2).

4）如果 |T1-T0|＞ε，转步骤5）；否则，转步骤6）.

5）如果n≤M,则n=n+1，h=2-n,T0=T1,T1(f(a-h)-2f(a)+f(a+h))∕(h2)，转步骤4）；否则，输出出错信息，转步骤7）.

6）输出计算结果T1.

7）结束.

3.2 步长最接近最优步长时终止计算

在步长逐步减半并接近最优步长hopt过程中，计算精度将越来越高，而步长小于hopt后，继续对步长减半数值计算的误差将会不断增大.因此，经n-1次步长减半后得到的步长hn-1与最优步长hopt若满足如下关系

相应的导数近似值则满足如下条件

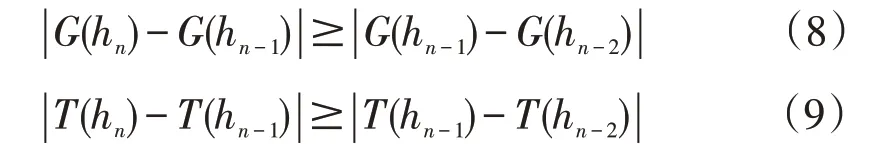
此即步长最接近最优步长时变步长数值微分法的计算终止条件,G(h)为步长为hn-1时f′(a)的近似值.

上述算法既可避免直接确定最优步长，又可获得具有较高计算精度的计算结果，因而是一种非常实用的有效算法.

若以步长最接近最优步长作为计算终止条件，用变步长中点公式计算函数f(x)在点a的一阶导数的算法可描述如下：

算法2：数值微分的变步长中点公式算法

1）输入函数f(x)，输入点a的值.

2）步长减半次数n=0，h=2-n=1，计算G0=[f(a+h)-f(a-h)]∕(2h).

3）步长减半：n=0，h=2-n=1∕2，计算G1=[f(a+h)-f(a-h)]∕(2h).

4）n=n+1，h=2-n，计算Gn=[f(a+h)-f(a-h)]∕(2h).

5）如果 |Gn)-Gn-1|≥ |Gn-1-Gn-2|，转步骤6）；否则，转步骤4）.

6）输出计算结果Gn-1.

7）结束.

4 说明性算例

算例1用变步长三点公式计算函数f(x)=ex在输入的点x处的二阶导数近似值，要求误差不超过0.5×10-6及0.5×10-9，并统计步长减半次数.

解 根据算法1编写C语言程序生成Threepoints.com文件，计算结果如下：

请输入要计算二阶导数值的点a:1

请输入精度要求epsilon:0.0000001

点a=1.000000处的二阶导数为f′′(a)=2.7182818353，步长共减半11次.

请输入要计算二阶导数值的点a:1

请输入精度要求epsilon:0.000000001

步长减半次数已达25次，仍未达到精度要求.

算例2取初始步长h0=1，用变步长中点公式计算函数f(x)=x2e-x在点x=1.0,1.5,…,5.0处的一阶导数及误差,并统计对应的最佳步长.

解 根据算法2编写C语言程序生成文件Midpoints.com，计算结果如下：

5 总结

本研究提出了中心差商公式变步长算法计算机实现时的两种计算终止条件，若以计算结果满足精度要求作为计算终止条件，可避免直接计算最优步长，方法简单，设计程序方便，可以获得满足一般精度要求的计算结果.但当要求的精度很高时，此方案的计算精度可能不能令人十分满意.若以步长最接近最优步长作为计算终止条件，既可避免直接确定最优步长，又可获得具有较高计算精度的计算结果，因而是一种非常实用的有效算法.