基于贝塔分布的最优置信区间研究
温利民,张良超,章 溢,刘 蔚
(1.江西师范大学数学与统计学院,江西 南昌 330022;2.江西师范大学财政金融学院,江西 南昌 330022)
0 引言
在概率论与数理统计中,区间估计是参数估计的重要内容.设θ是总体的一个未知参数,在总体为连续型分布的情况下,通过枢轴量法可得到参数的置信区间.然而当枢轴量的分布为单峰非对称时,利用传统方法构造的区间是等尾置信区间,而不是最优置信区间.
关于最优置信区间的定义,常见的有2种:一种是在给定置信水平的区间估计下要求平均区间长度最短,另一种是在给定平均区间长度下要求置信度尽可能大或精确度尽可能高.本文主要考虑第1种定义,即在给定置信度水平下求解平均值区间长度最短的区间估计.在数理统计中,关于置信区间的最优性的研究较多.夏乐天等[1]讨论了指数分布参数的最短区间估计;袁长迎等[2]在伽玛分布形状参数已知时研究了尺度参数的最短区间估计;徐美萍等[3]研究了在威布尔分布中尺度参数的最短区间估计;王秀丽[4]研究了均匀分布参数的最短置信区间;薛峰等[5]利用粒子群优化算法研究了贝塔分布参数的最短置信区间.在区间估计问题中,枢轴量G的分布通常是单峰分布,如正态分布、t分布、卡方分布、F分布等.由于正态分布和t分布是单峰对称分布,且未知参数θ在枢轴量G的分子上,所以用传统方法构造的区间就是最短置信区间.然而由于卡方分布和F分布为单峰非对称分布,所以传统方法构造的区间不是最短置信区间.孙鹏哲等[6]研究了卡方分布的最短置信区间,得出在各种自由度和常用的置信水平下最优左侧尾概率分配统计表.李广正[7]运用拉格朗日乘数法和利用Mathematica软件给出了F分布的最短区间估计用表.上述文献对于F分布和卡方分布的最短置信区间讨论较多,而对于贝塔分布的研究较少.
在已有的研究基础上,本文给出在一类形状参数下基于贝塔分布的最短置信区间,这可以适用于当枢轴量服从贝塔分布时求解最短置信区间.利用具有单峰的贝塔分布的密度函数,可得到待估参数的最短置信区间.此外,在贝叶斯框架下,当参数的后验分布服从贝塔分布时,可得到参数的最短后验区间估计.通过模拟分析,验证贝塔分布的最短置信区间的优越性.
1 最短置信区间的概念界定
1.1 区间估计的定义及说明
定义1设总体X具有概率函数f(x;θ),θ为未知参数.X1,X2,…,Xn是取自总体X的一个样本,若对于事先给定的α(0<α<1),存在2个统计量
T1=T1(X1,X2,…,Xn)与T2=T2(X1,X2,…,Xn)
使得P(T1≤θ≤T2)=1-α成立,则称区间[T1,T2]为参数θ的置信水平为1-α的置信区间,其中T1和T2分别被称为置信水平1-α的置信下限和置信上限.
由定义可以看出,T1和T2都是不依赖于未知参数的随机变量,因此置信区间[T1,T2]是随机区间.Pθ(T1≤θ≤T2)=1-α表示:对样本X1,X2,…,Xn观测多次,得到许多不同的区间[T1,T2],在这些确定的区间中,大约有(1-α)×100%的比例包含了未知参数θ的真值,而约有α×100%的比例不包含其真值.需特别注意,对于一次抽样所得到的一个区间,决不能理解为“不等式T1≤θ≤T2成立的概率为1-α”.因为在给定样本下的T1和T2是2个确定的数,从而只有2种可能:要么这个区间包含θ;要么这个区间不包含θ.因此,定义说明区间[T1(X1,X2,…,Xn),T2(X1,X2,…,Xn)]属于包含未知参数θ的区间类的置信水平是1-α,这也说明置信水平与概率是有所区别的,不可混淆.
1.2 区间估计的可靠度和精确度及其关系
当参数真值为θ时,自然希望随机区间[T1,T2]包含θ的概率Pθ(T1≤θ≤T2)要大.因此,一个好的区间估计应该对所有属于参数空间Θ的θ,概率Pθ(T1≤θ≤T2)都相当大.

若一个区间估计的置信系数越大,则该区间估计的可靠度越高.但是,构造一个置信系数很大的区间估计并不是一件难事.如将明天中午12点的气温估计在-10~50 ℃之间,这个估计的可靠度很高,但由于它的范围太大,很不精确,所以一个好的区间估计还有一个精确度的要求.
1.3 最短置信区间的确定
区间估计的精确度的标准不止一个,常用的标准有2个:
1)区间[T1(X1,X2,…,Xn),T2(X1,X2,…,Xn)]的平均长度Eθ[T2-T1]要短,即区间的范围不能太大,这是符合实际的;
2)设参数真值为θ,在θ*≠θ时,自然希望区间[T1,T2]包含θ*的概率要小,即区间[T1,T2]包含非真值的情况出现越少越好.
在给定样本容量n后,可靠度与精确度是相互制约着的.为了提高可靠度,可以通过增大区间范围来实现,但是会降低精确度.反过来,为了提高精确度,可通过减小区间范围来实现,但是会降低可靠度.为此本文采用J. Neyman建议的某种折中方案:在使得置信系数达到一定要求的前提下,寻找精确度尽可能高的区间估计,也就是要求区间平均长度尽可能短,或者区间包含非真值的概率尽可能小,这2个要求可能同时达到,也可能不同时达到.
下面介绍构造置信区间的常用方法,即枢轴量法.可按下列3个步骤构造η=g(θ)的置信区间.
1)构造样本(X1,X2,…,Xn)和未知参数η的一个函数G=G(X1,X2,…,Xn;η),要求G的分布与未知参数η无关,称具有这种性质的函数为枢轴量.
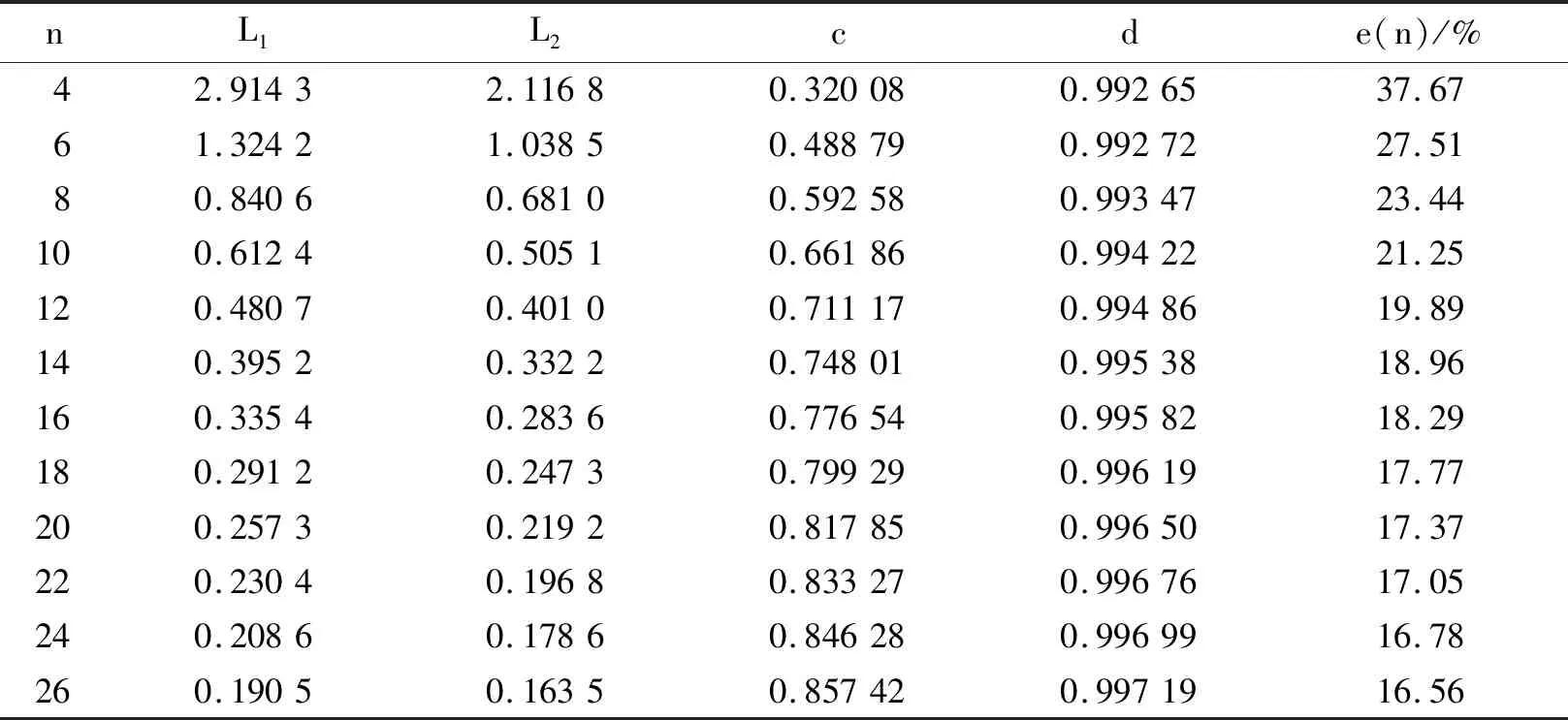
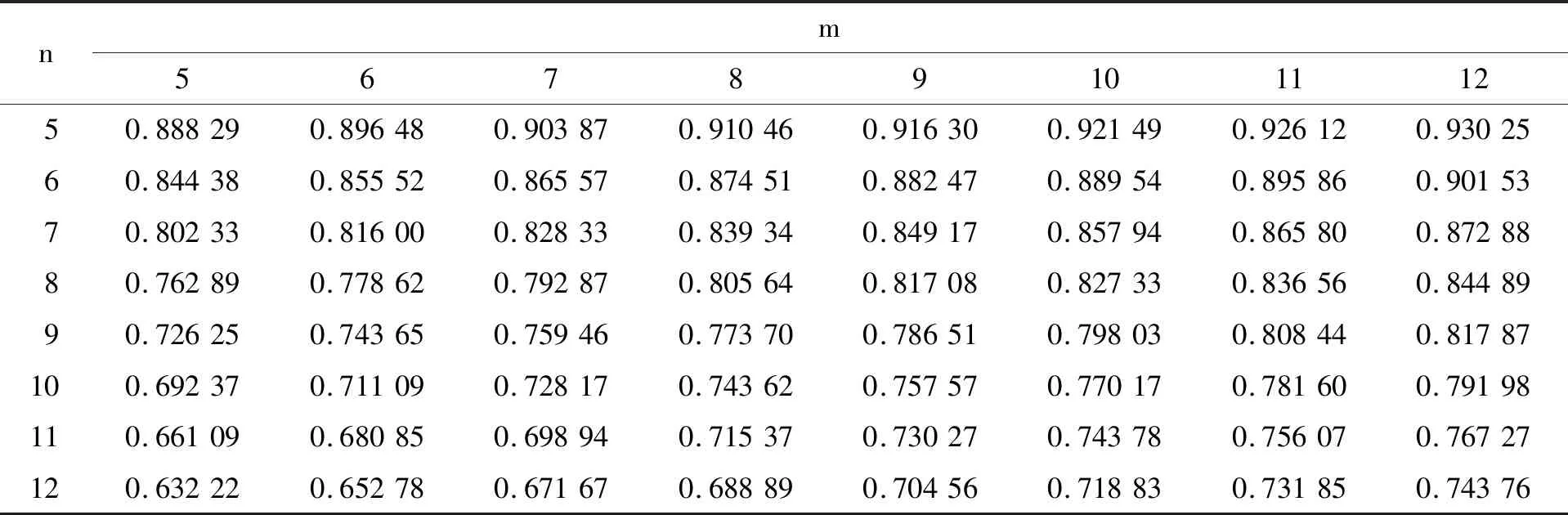
2)对给定的α(0<α<1),选取2个常数c和d(c Pθ(c≤G(X1,X2,…,Xn;η)≤d)=1-α,∀θ∈Θ. 3)若不等式c≤G(X1,X2,…,Xn;η)≤d可等价地变换为 T1(X1,X2,…,Xn)≤η≤T2(X1,X2,…,Xn), 则 Pθ(T1(X1,X2,…,Xn)≤η≤T2(X1,X2,…,Xn))=1-α,∀θ∈Θ, 从而[T1(X1,X2,…,Xn),T2(X1,X2,…,Xn)]是η的一个置信水平为1-α的置信区间.当G(X1,X2,…,Xn;η)是η的连续严格单调函数时,这2个不等式的等价关系总是可以做到的.当g(θ)=θ时,[T1(X1,X2,…,Xn),T2(X1,X2,…,Xn)]是θ的一个置信水平为1-α的置信区间. 一般来讲,满足要求的c和d是不唯一的,若有可能,应选在平均区间长度Eθ[T2-T1]达到最短时的c与d,则此时所求得的置信区间被称为置信水平1-α的最短置信区间.由于区间平均长度与所构造的枢轴量密切相关,所以接下来考虑在2类枢轴量形式下的最短置信区间估计.以下讨论都是在枢轴量服从单峰分布情况下进行的. 1)枢轴量G具有如下形式: G=T(X1,X2,…,Xn)(θ+U(X1,X2,…,Xn)), 其中T(X1,X2,…,Xn)>0. 由Pθ(c≤G≤d)=1-α(即Pθ(c≤T(θ+U)≤d)=1-α)得到参数θ的置信区间为[cT-1-U,dT-1-U],平均区间长度为(d-c)Eθ(T-1).考虑在平均区间长度最短下的区间估计,即为求如下条件极值问题: (1) 运用拉格朗日乘数法,令L=d-c+λ(F(d)-F(c)-1+α),对L关于c、d分别求偏导并令其为0得 (2) 其中F(·)、f(·)分别表示G的分布函数与密度函数.由式(2)可知,f(c)=f(d).所以条件极值问题(1)可转化为如下所示的2元方程组求解问题: (3) 当f(x)为单峰对称密度函数(比如正态分布、t分布的密度函数)时,由式(3)容易看出,此时等尾置信区间即为最短置信区间.当f(x)为单峰非对称密度函数(如卡方分布和F分布的密度函数)时,只要求解式(3)就可得最短置信区间,文献[8]证明了式(3)有唯一解,具体求解可利用求根法或黄金分割法[9]得到. 2)枢轴量G具有如下形式: G=T(X1,X2,…,Xn)(θ+U(X1,X2,…,Xn))-1, 其中T(X1,X2,…,Xn)≥0. 由Pθ(c≤G≤d)=1-α(即Pθ(c≤T(θ+U)-1≤d)=1-α,其中c、d同号)得到参数θ的置信区间为[d-1T-U,c-1T-U],平均区间长度为(c-1-d-1)Eθ(T).考虑在平均区间长度最短下的区间估计,即为求如下条件极值问题: (4) 同理运用拉格朗日乘数法,把条件极值问题(4)可转化为如下所示的2元方程组求解问题: (5) 当f(x)为单峰对称密度函数(如正态分布、t分布的密度函数)时,由式(5)容易看出,此时等尾置信区间对应的c、d满足f(c)=f(d),然而c2f(c)≠d2f(d),从而等尾置信区间不是最短置信区间,且文献[8]证明了式(5)有唯一解. 现有文献对于F分布和卡方分布的最短置信区间讨论较多,而对于贝塔分布的研究较少.事实上,贝塔分布在一类形状参数下也是单峰非对称分布.接下来研究在枢轴量服从贝塔分布时的最短置信区间,首先给出一个引理. 引理1[10]设总体X的密度函数为p(x),分布函数为F(x),X1,X2,…,Xn为样本,则样本极差Z=X(n)-X(1)的分布函数为 定理1设X1,X2,…,Xn是来自均匀分布U(θ1,θ2)的一个样本,则θ2-θ1的一个无偏估计为 证令Yi=(Xi-θ1)/(θ2-θ1),i=1,2,…,n,则Yi独立同分布于U(0,1),由引理1可知 Y(n)-Y(1)~Beta(n-1,2). 由贝塔分布的数学期望公式有 E(Y(n)-Y(1))=E((X(n)-X(1))/(θ2-θ1))=(n-1)/(n+1), 由定理1的证明过程知,事实上可构造枢轴量: G=(X(n)-X(1))/(θ2-θ1)~Beta(n-1,2). 对给定的置信水平1-α,若c、d满足 P(c≤G≤d)=1-α, 可得θ2-θ1的置信区间为 [(X(n)-X(1))d-1,(X(n)-X(1))c-1]. (6) 注意到,要使得式(6)的平均区间长度最短等价于求解式(5),其中F(·)为Beta(n-1,2)的分布函数,f(·)为Beta(n-1,2)的密度函数. 接下来讨论给定置信水平0.90和0.95以及样本容量n,比较θ2-θ1的最短置信区间与等尾置信区间.首先由式(6)知,平均区间长度正比于c-1-d-1,因此记等尾置信区间长度为 L1=(Betaα/2(n-1,2))-1-(Beta1-α/2(n-1,2))-1. 其中c、d是在式(6)中当平均区间长度达到最短时的取值,具体可通过Matlab软件中的解方程组命令fsolve求解,因此记最短置信区间长度为 L2=c-1-d-1. 2者的相对差异记为e(n)=(L1-L2)/L2.对不同的样本容量,得到如表1和表2所示的结果. 在表1、表2中的c、d是在式(6)中当平均区间长度达到最短时的取值.从表1、表2可以看出:在给定置信水平情况下,2种方法求得的置信区间长度都随着样本容量n的增加而变短,而且c、d也随着样本容量增加而变大.这是由于贝塔分布的形状参数n-1增加,其密度函数越呈现“尖峰左偏”形状,样本的集中趋势越来越明显. 表1 在置信水平0.90下最短置信区间与等尾置信区间的比较 表2 在置信水平0.95下最短置信区间与等尾置信区间的比较 通过对比可以看出:在每一个置信水平和样本容量的组合下,本文计算的最短置信区间要优于等尾置信区间,随着样本容量的增大,2种置信区间的相对差异逐渐减小,但即使样本容量取到26,在置信水平0.95的情况下相对差异仍有15.16%.在样本容量n≤10时,2者的相对差异更大,大多数达到20%以上.由于给定样本容量,在置信水平0.95情况下的2种置信区间的相对差异比在置信水平0.90的情况下的更小,所以,在小样本情况下最短置信区间优势明显. 事实上,当参数m>1、n>1时,贝塔分布Beta(m,n)都是单峰分布.如m>n>1是左偏单峰分布,n>m>1是右偏单峰分布,n=m>1是单峰对称分布.当枢轴量G具有如下形式: G=T(X1,X2,…,Xn)(θ+U(X1,X2,…,Xn))-1 且服从贝塔分布时,本文构造了在置信水平0.90和0.95下基于Beta(m,n)的最短区间估计用表,整理在表3~表6中. 表3 在置信水平0.90下最短置信区间的左侧端点值 表4 在置信水平0.90下最短置信区间的右侧端点值 表6 在置信水平0.95下最短置信区间的右侧端点值 从表3~表6可以看出:在给定置信水平情况下,n固定,m越大,最短置信区间的左侧端点值越大,最短置信区间的右侧端点值也越大,但增大幅度比左侧端点值更小.在给定置信水平情况下,m固定,n越大,最短置信区间的左侧端点值越小,最短置信区间的右侧端点值也越小,但减小幅度比左侧端点值更大.m和n都固定,在置信水平更高情况下的左侧端点值更小以及右侧端点值更大,这导致置信区间长度增大,这体现了可靠度与精确度其实是相互制约的. 前面的分析讨论都是在基于枢轴量的分布为单峰分布的假设下得到的.但当a>1时,Beta(a,1)分布的密度函数是单调递增的.接下来讨论当枢轴量服从Beta(a,1)分布时在2类枢轴量形式下的最短置信区间估计. 1)枢轴量G具有如下形式: G=T(X1,X2,…,Xn)(θ+U(X1,X2,…,Xn)), 其中T(X1,X2,…,Xn)>0. 由Pθ(c≤G≤d)=1-α(即Pθ(c≤T(θ+U)≤d)=1-α)得到参数θ的置信区间为[cT-1-U,dT-1-U],平均区间长度为(d-c)Eθ(T-1).此外,G的密度函数为 则寻求c、d使得 (7) 根据密度函数单调递增的特点,对于给定的置信水平,在平均区间长度最短下,应当选取g(x)取值较大的部分,即应选取c0,使得 (8) 其中c0=α1/a,得到参数θ的置信区间为[c0T-1-U,T-1-U],平均区间长度为(1-c0)Eθ(T-1).由于密度函数严格单增,所以观察式(7)和式(8),显然有d-c≥1-c0.综上所述,此时的最短置信区间为[c0T-1-U,T-1-U]. 2)枢轴量G具有如下形式: G=T(X1,X2,…,Xn)(θ+U(X1,X2,…,Xn))-1, 其中T(X1,X2,…,Xn)≥0. 若Pθ(c≤G≤d)=1-α(即Pθ(c≤T(θ+U)-1≤d)=1-α)得到参数θ的置信区间为[d-1T-U,c-1T-U],平均区间长度为(c-1-d-1)Eθ(T).令 所以(d-c)/(cd)≥(1-c0)/c0. 对于区间估计问题,在上述讨论中把参数看成一个常数,在求置信区间时要构造一个枢轴量,这一点技巧性较强,有时是比较困难的.并且在理解置信水平和置信区间时也会产生困难,而贝叶斯方法具有处理方便和含义清晰的优点.贝叶斯统计方法是英国统计学家托马斯·贝叶斯(Thomas Bayes)提出的一种方法,其主要的核心思想是将未知参数看成随机变量.这使得统计学的区间估计得到了更好的解释.贝叶斯统计方法已成为现代统计学不可或缺的重要内容,在数理统计、生物统计、医学统计、环境统计、金融统计与精算等领域[11-15]中都有广泛的应用. 若参数θ的先验分布为π(θ),样本分布函数为F(x;θ),由贝叶斯定理可得参数θ的后验分布π*(θ|x).若给定概率1-α,找到一个区间[c,d],使得P(c≤θ≤d|x)=1-α成立,这样求得的区间就是参数θ的贝叶斯置信区间,称1-α为置信水平.注意到,在贝叶斯统计中,把参数θ看成是随机变量,直接从后验分布中推导得出置信区间,并且把置信水平1-α很自然地解释为参数落入这一区间的概率. 置信水平和平均区间长度是评价贝叶斯区间估计的2个标准,在置信水平给定的情况下,希望平均区间长度越短越好.接下来,考虑在参数θ的后验分布为贝塔分布时的最短后验区间估计. 设X1,X2,…,Xn是来自负二项分布NB(m,θ)的样本,其分布函数为 给定置信水平1-α,若P(c≤θ≤d|x)=F(d)-F(c)=1-α,则得到θ的贝叶斯置信区间为[c,d],区间长度为d-c.欲求最短置信区间,即为求如下条件极值问题: (9) 运用拉格朗日乘数法,把条件极值问题(9)可转化为如下所示的2元方程组求解问题: 其中F(·)、f(·)分别表示Beta(a*,b*)的分布函数与密度函数. 假设某企业生产的圆盘直径服从均匀分布U(c,d),实际统计14个该种圆盘直径,数据如下:8.022 2,7.965 0,8.016 0,8.001 9,8.047 3,8.014 9,8.030 0,7.995 4,7.993 2,8.032 5,7.958 3,7.963 3,7.967 3,7.989 1. 由定理1得到d-c的估计值为0.102 7.当置信水平为0.90时,经过简单计算,等尾置信区间为[0.091 4,0.126 5];查表1可知,最短置信区间为[0.089 4,0.119 0].同理计算,当置信水平为0.95时,等尾置信区间为[0.090 6,0.134 6],最短置信区间为[0.089 2,0.126 7].以上结果表明:当置信水平为0.90和0.95时,本文方法得到的置信区间长度比等尾置信区间长度更短,且它们的长度之比分别为0.843 3和0.852 3,由此可见这种误差是不可忽略的. 通过上述分析可以看出:研究在枢轴量服从贝塔分布时的最短置信区间是十分有必要且有意义的,尤其是当样本容量较小时.本文介绍的方法在理论上可以计算在更广泛的参数组合下的贝塔分布的最短置信区间.

2 贝塔分布的最短置信区间
2.1 单峰贝塔分布的最短置信区间

2.2 与等尾置信区间的比较



2.3 Beta(a,1)型的最短置信区间


2.4 最短后验置信区间



3 数值例子
4 总结

