一类线性权互补问题的修正全牛顿步可行内点算法

吴昕阳， 张睿婕， 迟晓妮， 王博妲

(桂林电子科技大学 数学与计算科学学院,广西 桂林 541004)

权互补问题(weighted complementarity problem, 简称WCP)是一类新的优化问题，目前关于权互补问题的理论和算法研究较少。Potra[1]最先提出权互补的概念，即找到一对属于一个流形与一个锥的交集的向量，使得它们在某个代数中的乘积等于一个给定的权向量。当权向量为零向量时，权互补问题退化为互补问题。Potra[1]将Fisher市场均衡问题、二次规划与权中心问题转化为单调线性权互补问题，并提出了求解单调线性权互补问题的2种内点算法。之后，Potra[2]又证明了充分线性权互补问题的一些基本结论，设计了一种校正-预估内点算法。目前,光滑牛顿法[3,9]和内点算法[10]是求解线性优化、互补问题[11-12]和权互补问题[13]等的有效算法，其中内点算法由于具有多项式时间复杂度[14]而备受关注。Kojima等[4-5]给出了线性互补问题的原对偶内点算法及其复杂度。Roos等[6]首次提出了线性规划的全牛顿步可行内点算法。随后，Zhang等[7]基于修正牛顿方向提出了新的全牛顿步可行内点算法。Xu[8]给出了线性规划的基于修正全牛顿方向的不可行内点算法，并证明了该算法在适当条件下具有良好的复杂度上界。Asadi 等[15]提出了求解单调线性权互补问题的全牛顿步可行内点算法。

鉴于此，基于Xu[8]提出的修正全牛顿步，提出一种求解非负象限上线性权互补问题(LWCP)的可行内点算法。本算法采用修正全牛顿步，避免了线性搜索，简化了算法分析，且保证了迭代点都位于中心路径的窄邻域内，最后分析了算法的可行性、收敛性及复杂度。数值算例结果表明，本算法是有效的。

1 权互补问题

考虑Rn上的LWCP[1]：找到一向量对(x,y,s)∈Rn×Rm×Rn使得

(1)

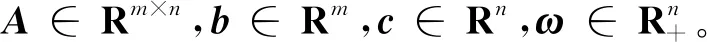
定义LWCP(1)的严格可行域为

1.1 中心路径及搜索方向

由于直接求解LWCP(1)比较困难，用xs-ω=μe代替xs-ω=0,求解方程组

(2)

假定A是行满秩矩阵，即R(A)=m。若内点条件(IPC)[6]成立，即(x,y,s)∈F0,则对任意参数μ>0,方程组(2)有唯一解(x(μ),y(μ),s(μ)),称之为LWCP(1)的μ-中心。所有μ-中心的集合{(x(μ),y(μ),s(μ))|μ>0}称为LWCP(1)的中心路径。当μ→0时，中心路径的极限点便是LWCP(1)的最优解。当xs-ω≥0时，定义

(3)

当υ≥0时，易证

xs-ω=μe⟺υ2=e⟺υ=e⟹υ2=υ。

则方程组(2)可化为

(4)

其中，μ+=(1-θ)μ,θ∈(0,1)。因而，通过求解方程组

(5)

可得牛顿搜索方向(Δx,Δy,Δs)。

定义

(6)

由式(3)、(6)，方程组(5)可化为

(7)

定义邻近测度

(8)

引理1[6]若u与v正交，则

因为dx与ds正交，由引理1和式(8)可得

(9)

同理可得

引理2[7]对任意υ∈Rn,有

1-δ(υ)≤υi≤1+δ(υ),i=1,2,…,n。

1.2 修正全牛顿步可行内点算法

设μ0>0,(x0,y0,s0)∈F0,选择适当参数θ,ε,τ,使得

δ(x0,s0,μ0)≤τ。

在修正全牛顿步中，求解方程组(5)得牛顿搜索方向(Δx,Δy,Δs),其中μ+=(1-θ)μ,θ∈(0,1)。令新迭代点

(10)

满足内点条件，且

δ(x+,s+;μ+)≤τ，

当‖xs-ω‖≤ε时，算法迭代终止。

算法1求解LWCP的修正全牛顿步可行内点算法

2)当‖xs-ω‖≤ε时，算法终止，否则，转步骤3)。

3)求解方程组(5)，得搜索方向(Δx,Δy,Δs)。令

2 算法分析

2.1 可行性和收敛性分析

引理3若‖dxds‖∞<(1-θ)(1-δ(υ)),则(x+,y+,s+)∈F0。

证明令α∈[0,1],记

x(α)=x+αΔx,y(α)=y+αΔy,s(α)=s+αΔs。

则由式(3)、(6)和方程组(7)中第3式得

(11)

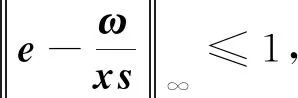
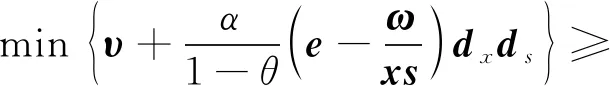
(12)

又因为(1-α)υ2>0,所以由式(12)、(13)知，若

‖dxds‖∞<(1-θ)(1-δ(υ)),

(13)

则x(α)s(α)-ω>0。

由于x(0)=x>0,s(0)=s>0,且x(α),s(α)与α呈线性关系，对α∈[0,1]，有x(α)，s(α)>0。相应地，x(1)，s(1)>0。证毕。

证明由式(9)和引理3知，若

(14)

(15)

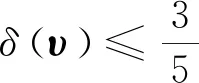
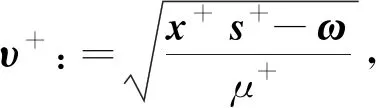
证明由式(11)得

引理6若(x+,y+,s+)∈F0,则

证明由引理5知，

因此，

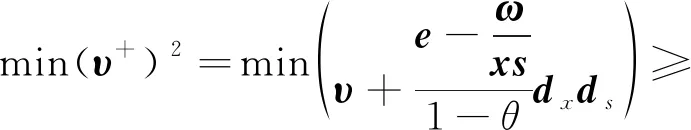
由引理2可得

引理7若(x+,y+,s+)∈F0,则

证明由引理5得

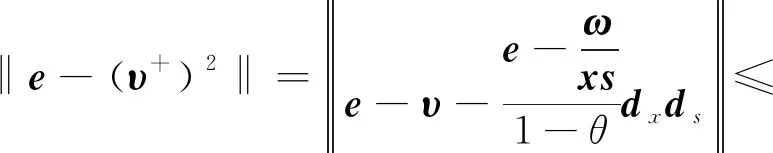
证明由δ(υ+)的定义式(8)得

因此，由引理6得

由式(9)、(*)可知，

(16)

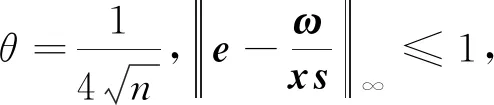
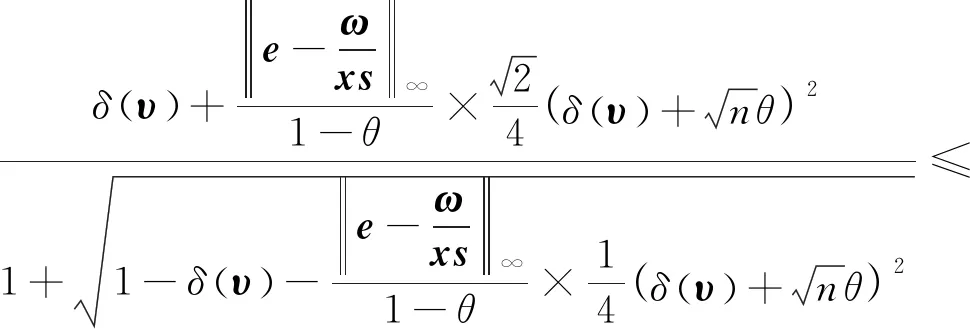
(17)

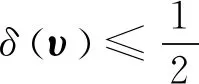
(18)

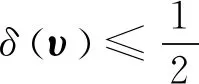
2.2 复杂度分析

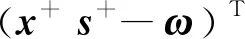
(19)

又由引理5得

(1-θ)nμ‖υ‖∞+nμ‖dxds‖∞。

(20)

则根据式(12)、(21)和引理2 可知，

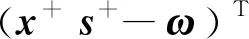
[2(1-θ)nμ]2。

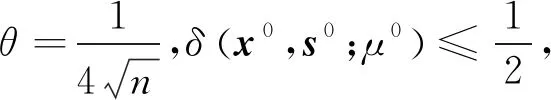
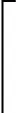
次迭代，才能得到LWCP(1)的ε-近似解。

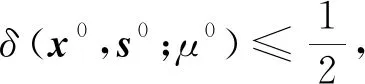
因此要使‖xksk-ω‖≤ε,只需

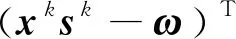
[2(1-θ)nμk-1]2=[2(1-θ)knμ0]2。

3 数值算例

为检验算法1的有效性，运用MATLAB R2016b编程，在Intel®Core i5 CPU 2.3 GHz，8.0 GiB内存，IOS操作系统的计算机上进行数值实验。随机生成5个不同规模的LWCP(1)，对每种规模产生10个问题进行求解。

任意选取参数μ0>0,起始点(x0,y0,s0)及权向量ω≥0，使得δ(x0,s0;μ0)≤τ。随机生成行满秩矩阵A∈Rm×n。令b=Ax0,c=ATy0+s0,即初始点满足内点条件。算法的终止条件为‖xs-ω‖≤ε，记Gap=‖xs-ω‖。在算法1中取参数

表1为算法1求解不同规模的LWCP(1)的数值结果，其中数据为10次结果的平均值。

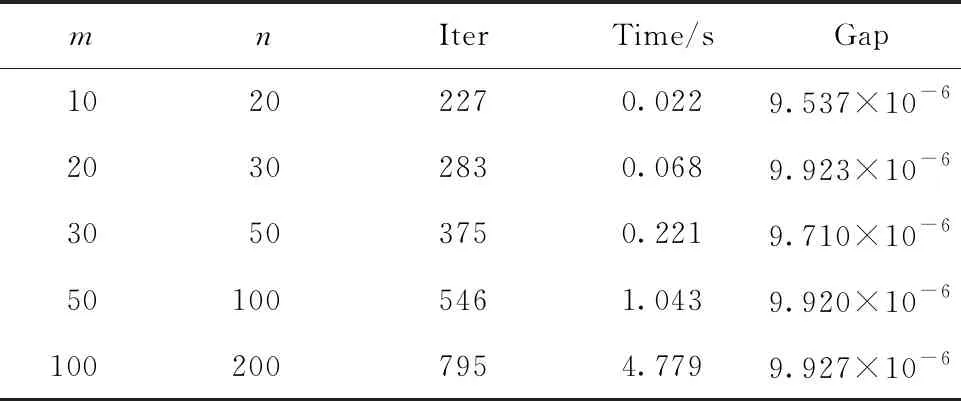
表1 求解不同规模线性权互补问题的数值结果

例1考虑R3上的LWCP(1)，其中

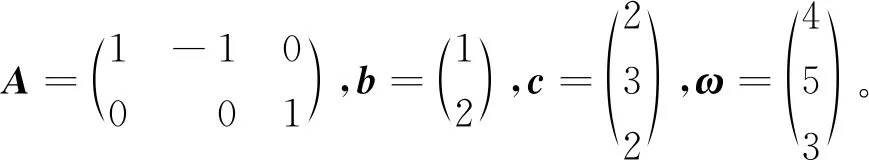
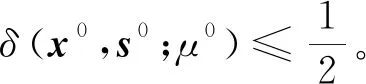
x*=(2.477,1.477,2.000)T,y*=(0.385,0.499)T,s*=(1.615,3.385,1.500)T。图1为迭代过程中邻近测度及Gap的值。从图1可看出，随着μ的减小，邻近测度和Gap逐渐减小，并趋于0。

图1 迭代过程中邻近测度及Gap的值

4 结束语

提出了求解一类线性权互补问题的一种修正全牛顿步内点算法。该算法基于中心路径的等价变换，得到搜索方向。证明了算法经过修正全牛顿步后生成的迭代点仍严格可行，且具有多项式时间复杂度。数值算例表明了算法的可行性。