精心设计教学 实现减负增效
——以高中数学教学为例

丁建兵

江苏省西亭高级中学 226301

在数学教学中，部分教师过分强调解题教学的重要性而忽视了数学的应用价值，限制了学生的数学运用能力的发展，影响了学生数学素养的提升，使得教学内容空洞、枯燥，严重影响了课堂效率.为了改变这一现象，笔者在教学过程中做了一些尝试，提出了一些建议，供参考！

营造自由氛围，激发学习兴趣

数学是一门非常重要的基础学科，它与其他学科紧密相连，与我们的生活息息相关，具有重要的应用价值.其实，数学并没有我们想象中那么抽象，但为什么大多数师生都常以抽象和复杂来评价数学呢？究其原因，主要是在功利教学长期的影响下，学生的主要精力都在解题上，很少关注数学的应用性，脱离了实际应用的数学学习自然显得抽象.因此，在数学教学中可以适当地创设一些情境，引入一些数学故事，淡化数学的抽象感，调动学生学习的积极性.

案例1自然数平方和公式12+22+32+…+n2=的证明.

自然数平方和公式学生都能熟练掌握，但是对于公式的证明过程很多学生都感觉很陌生，遇到类似问题的证明时也常感觉束手无策，出现这一现象主要与教师的教学方式有关，大多数教师为了掌控教学进度，在教学过程中更加关注结论的应用，“刷题”成了知识强化的主要手段，学生的学习热情难以被激发，课堂效率低下.为了改变这一现象，教师要放手让学生利用已有经验去尝试证明，给学生营造一个更为广阔的空间，这样更容易点燃学生的学习热情，更能活化学生的思维，学生的思维一旦打开了，学习效率自然就提高了，这样不仅不会浪费学习时间，而且有利于学习能力提升.

在案例1的证明过程中，教师放手让学生尝试自主探究，因此涌现出了不同的证明思路.经过学生思考、交流和总结，教师及时做好补充和点评，使数学知识得以内化.为了丰富学生的认知，拓宽学生的视野，教师在教学中可以多让学生了解一些数学文化，进而提升学生的数学素养.例如，本案例教学中，教师列举了一些数学家对该公式的证明，如法国数学家帕斯卡的“恒等式法”，美国数学家波利亚的“观察、猜想、数学归纳法”，我国北宋时期数学家的“堆垛法”，等等，让学生在借鉴和吸收中不断丰富认知，促进数学学习能力提升.

以生为主，培养数学思维品质

在数学教学中，教师切忌用自己的思路去限制学生，若学生的思路被教师牵着走，则很难培养出个性张扬、具有创新精神的人才.在数学教学中，应采用更加多样化的教学手段来培养和激发学生的探究热情，多从学生的角度去思考问题、设计问题，从而体现学生的主体地位.在数学教学中，当学生给出的解题思路较为烦琐时，教师不要急于打断，应允许学生有不同的见解；当学生思路出现错误时，教师需要耐心聆听，找到出错的根源，并利用好错误资源避免同样的错误再次发生；当学生思维受阻时，可以顺着学生的思路适时地进行引导，帮助学生找到解题的突破口.只有处处体现出学生的主体地位，学生学习的积极性才能真正地被调动起来，从而挖掘出内在的潜能.当然，在数学教学中，要注意数学思想方法的渗透，引导学生从本质上去思考并解决问题，从而提高数学教学有效性.

案例2如图1所示，在直角坐标系xOy中，点A的坐标为（0，3），l的直线方程为y=2x－4.设圆C的半径为1，圆心C在l上.

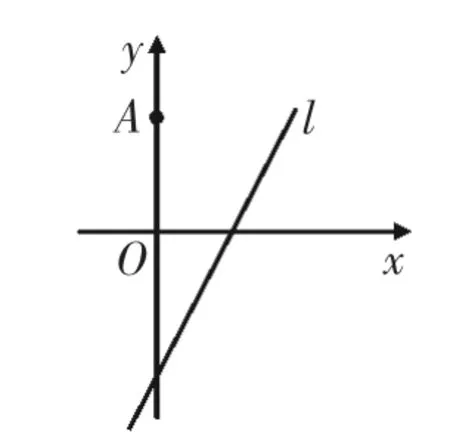
图1

（1）若圆心C也在直线y=x－1上，过点A作圆C的切线，求切线方程；

（2）若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围.

分析：对于问题（1），联立两直线方程可以求得圆心C（3，2），接下来利用点斜式求切线方程，求解过程中需要对斜率k分情况进行讨论，分类讨论思想蕴含其中.对于问题（2），首先根据已知求出点M的运动轨迹是以（0，－1）为圆心，半径为2的圆.又点M在圆C上，这样就将原问题转化为两圆的位置关系问题，转化后的解题思路更加清晰明了，转化思想在解题中起到了积极的作用.可见，数学思想方法在解题中无处不在，教学中要重视渗透和提炼，从而在数学思想方法的指引下形成良好的数学思维品质，促进学习能力提升.

借助变式训练，实现减负增效

变式训练是数学教学的常用手段之一，若在概念教学中应用变式，可有效帮助学生挖掘出概念的内涵及外延；若在公式、定理教学中应用变式，不仅有利于学生深化理解，而且可以帮助学生灵活运用；若在解题教学中应用变式，可以让学生在区别和联系中发现问题的本质，找到解题的捷径.因此，教学中教师可以精心设计一些变式训练，这样不仅可以达到深化理解的效果，而且有助于避免“题海战术”给学生带来的枯燥感，有助于提升学习信心.

案例3探究等差数列的通项an和Sn.

数列教学中往往会涉及很多概念和公式，为了让学生在深化理解的同时可以灵活应用，教学中常采用变式训练来巩固应用，强化理解.

分析：本题设计的目的是让学生巩固等差数列求和公式，摆脱思维定式的困扰，灵活运用相关的定理性质高效解决问题.在变式题目求解过程中，可设Sn=kn（7n+45），Tn=kn（n+3），则an=Sn－Sn－1（n≥2），b2n=T2n－T2n－1，这样代入后运用分离常数法可以求得n.通过变式训练让学生知道，有时候看似相同的问题其求解思路可能截然不同，因此数学学习中切勿死记硬背、机械套用，要灵活把握，深入理解，这样才能避免走弯路、走错路.

寻找错因，提高学习效率

出现错误在学习过程中是不可避免的，错误是学习过程的必然产物，因此教学中要善于发现错误、正视错误、善待错误.在教学过程中，常常会遇到这样的烦恼：有些错误明明重点讲解过，也进行了强化练习，然学生还是屡屡犯错.出现这一现象的主要原因是教师不够了解学生，在错误讲解时没有从学生的学情出发进行深入透彻的剖析，每次只是强调如何订正错误，而没有发现真正的错因，学生对错误的认识缺乏深刻性，致使没有真正地学懂吃透，从而出现了“一错再错”的现象.因此教学中必须对学情做到精准定位，充分展现错误产生的过程，找到真正的错因，从而制定有效的策略进行引导，带领学生走出误区，避免再次犯错，有效提高学习效率.

案例4已知x2+（1+2i）x－（3m－1）i=0有实根，求纯虚数m的值.

错解1：因为方程有实根，所以Δ≥0，所以（1+2i）2+4（3m－1）≥0，解得m≥

分析：出现这样错解的主因就是学生在学习中形成了思维定式，看到方程有实根就直接应用Δ≥0来判断，未从实际情况出发，没有抓住问题的本质特征.要知道本题中x的系数含有虚数，用Δ≥0的思路进行求解就相当于比较虚数的大小，学生单纯地考虑实数根却忽略了虚数的性质，由于基础知识掌握不牢而造成了错误.

错解2：将原式x2+（1+2i）x－（3m－1）i=0转化为复数形式，则有x2+x+（2x－3m+1）i=0，然后令x2+x和2x－3m+1都为0.

分析：本题中x2+x是实数，然2x－3m+1为虚数，因此应用两个复数相等的思路进行求解是错误的.

这样，找到错因后，学生解题就可以设纯虚数m=ai，其中a≠0且a∈R，则有x2+x+3a+（2x+1）i=0，求得m=

在数学学习过程中出现错误并不可怕，可怕的是学生不找错因，只是盲目地订正，这样的学习方式是机械的，很难学懂吃透，容易再错.因此，教学中必须合理地应用好错误，引导学生分析出自己的认知漏洞，从而有效地进行查缺补漏，强化理解.

总之，解题虽然是高中阶段应用数学的直接表现形式，但并不是数学学习的全部，教师要发挥好学生的主体地位，通过有效的拓展和延伸，激发学生的学习兴趣，让学生的数学素养潜移默化地得到提升.