G-非扩张映射有限族的多步迭代方法及其数值实验
高兴慧,何纪元,任欣怡,杨大庆,赵海洋,樊子秋,贾倩倩
(延安大学 数学与计算机科学学院,陕西 延安 716000)
0 引言
不动点理论在很多领域都有重要的应用,不动点的迭代方法是不动点理论研究的重要课题。2008年,Jachymski[1]将不动点理论与图论结合起来,随后,一些学者在具有有向图的Banach 空间中研究了G-非扩张映射的不动点的迭代逼近问题[2-7]。最近,Sridarat 等[2]构造了关于3个G-非扩张映射的SP迭代,具体如下:
(1)
其中{αn},{βn},{γn} 是[0,1]中的实序列。
Yambangwai 等[3]给出了关于3个G-非扩张映射的修正的三步迭代方法, 具体如下:
其中{αn},{βn},{γn}是[0,1]中的实序列。
受上述工作的启示, 本文将构造G-非扩张映射有限族的公共不动点的多步迭代方法,具体如下:
(2)
并证明该算法的强、弱收敛定理,最后给出数值例子验证该方法的优点。该文的主要结果是文献 [2-4] 的相关结论的改进。
1 预备知识

E(G-1)={(x,y)∈X×X:(y,x)∈E(G)}
若对∀x,y,z∈V(G),如果 (x,y),(y,z)∈E(G),那么 (x,z)∈E(G),则称有向图G=(V(G),E(G))是可传递的。
设x0∈V(G) 且A是V(G)的子集, 若对每一x∈A,有(x0,x)∈E(G),则称A是由x0主导的。若对每一x∈A,有 (x,x0)∈E(G),称A主导x0。
定义1[3]T:C→C称为G-非扩张的,若T满足下列条件:
(i)T保留G的边界,即 (x,y)∈E(G)⟹(Tx,Ty)∈E(G);
(ii)T不增加G的边权值,即 (x,y)∈E(G)⟹‖Tx-Ty‖≤‖x-y‖。
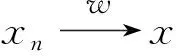

定义3[2]设C是实一致凸 Banach 空间的非空闭凸子集,C中的映像Ti(i=1,2,…,N) 满足条件C:若存在非减泛函f:[0,∞)→[0,∞) 满足f(0)=0 且f(r)>0,∀r>0,使得对 ∀x∈C,有
max{‖x-T1x‖,…,‖x-TNx‖}≥f(d(x,F))
其中F=F(T1)∩…∩F(TN),F(Ti) 是Ti的不动点集且d(x,F)=inf{‖x-q‖:q∈F}。
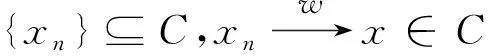

引理2[3]设 {an} 和 {tn} 是2个非负实数序列,满足下列不等式:
an+1≤an+tn,∀n≥1


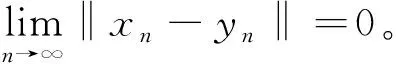

2 主要结果
在这一节中,设C是带有有向图G的Banach空间X的非空闭凸子集,使得V(G)=C且E(G)是凸集,图G是可传递的,Ti(i=1,2,…,N):C→C是G-非扩张映射,F=F(T1)∩…∩F(TN) 非空。任意x0∈C,{xn} 是由多步迭代(2)式生成的序列。

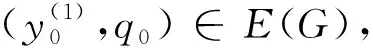


引理6 设X是一致凸 Banach 空间,实序列 {αn,1}…{αn,N}⊂[δ,1-δ],这里δ∈(0,1),且(x0,q0),(q0,x0)∈E(G),如果对于 ∀x0∈C,q0∈F,那么
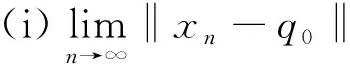
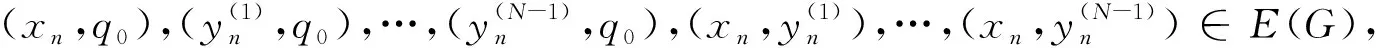
=‖(1-αn,1)(xn-q0)+αn,1(T1xn-q0)‖
≤(1-αn,1)‖xn-q0‖+αn,1‖T1xn-q0‖
≤(1-αn,1)‖xn-q0‖+αn,1‖xn-q0‖
=‖xn-q0‖
(3)
(4)

应用数学归纳法可得
(5)
于是
(6)

(7)
另外,由Ti(i=1,2,…,N) 的G-非扩张性可得
(8)
(9)
(10)
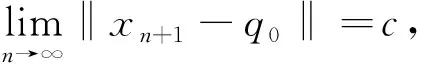
(11)
由(8)、(9)、(11) 式及引理3可得
(12)

(13)
由(10)、(13) 式可得
(14)
由(3)、(14) 式可得
(15)

(16)
(17)
由(4)、(17)式可得
(18)
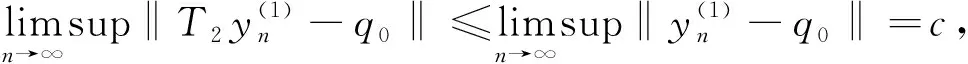
(19)
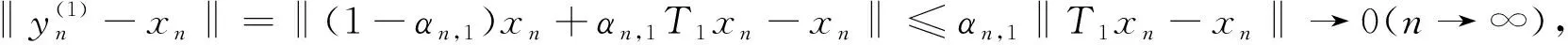
(20)

(21)
则有
(22)

(23)

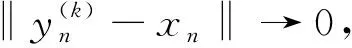
因此
(24)
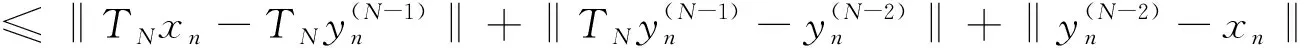

定理1 设X是满足Opial's条件的一致凸 Banach 空间,且C具有性质G,{αn,1},…,{αn,N}⊂[δ,1-δ],其中δ∈(0,1),对 ∀x0∈C,q0∈F,若 (x0,q0),(q0,x0)∈E(G),那么由算法(2)式生成的序列 {xn} 弱收敛于T1,T2,…,TN的公共不动点。

定理2 令X是一致凸 Banach 空间,{αn,1},…,{αn,N}⊂[δ,1-δ],其中δ∈(0,1),Ti(i=1,2,…,N) 是G-非扩张映射且满足条件C,F是由x0主导的且F主导x0,那么由算法(2)式生成的序列 {xn} 强收敛于T1,T2,…,TN的公共不动点。
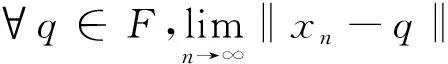
注1 (i)定理1和定理2分别将文献[2]中的定理3.8和定理3.7从3个G-非扩张映射的公共不动点的迭代方法推广到了G-非扩张映射有限族的公共不动点的迭代方法;
(ii)定理1和定理2也分别将文献[3]中的定理1和定理3从3个G-非扩张映射的公共不动点的迭代方法推广到了G-非扩张映射有限族的公共不动点的迭代方法。
3 数值实验
定义5[8]设C是 Banach 空间X的非空闭凸子集,且T:C→C是映射,假设 {xn},{zn} 是收敛于T的不动点q的2个迭代序列,如果对所有的n≥1,有‖xn-q‖≤‖zn-q‖,则称{xn} 收敛于q的速度快于 {zn}收敛于q的速度。


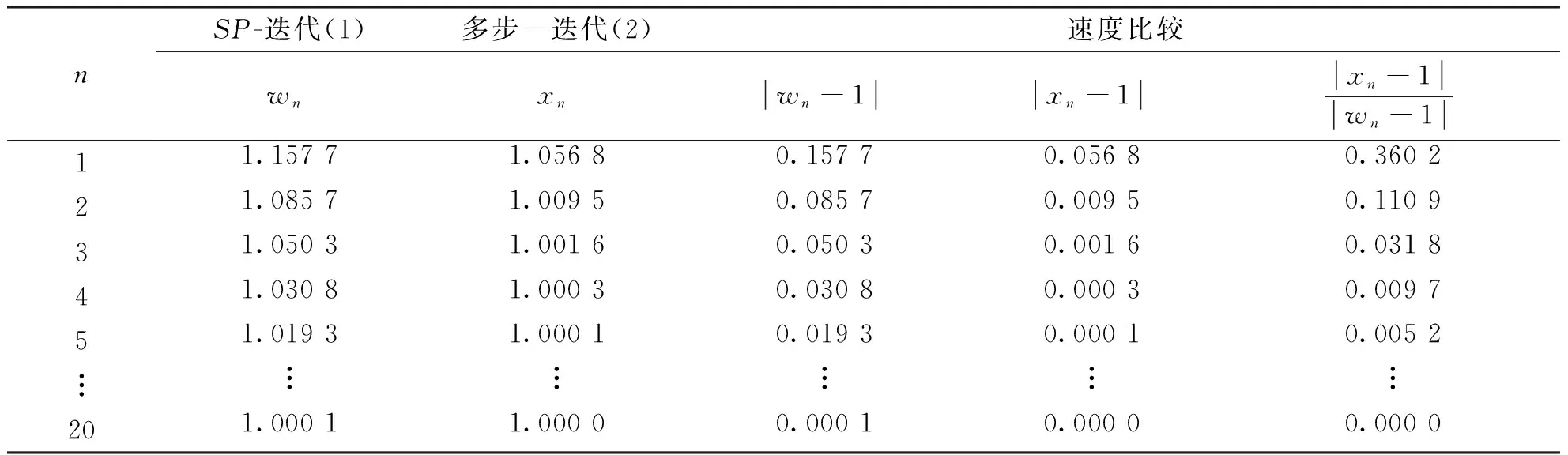
表1 利用定义5和定义6得出SP迭代 (1)和多步迭代(2)的收敛速度比较Tab.1 Comparison of rate of convergence of SP-iteration (1) and multi-step iteration (2)

