平面图的动态染色
卜月华, 杨瑞盈
(1.浙江师范大学 数学与计算机科学学院,浙江 金华 321004;2.浙江师范大学 行知学院,浙江 兰溪 321100)
0 引 言
本文考虑有限简单图.对于一个图G,把它的顶点集、边集、面集、顶点v的度、顶点v的邻点集及围长分别记作V(G),E(G),F(G),dG(v),NG(v)及g(G),在不引起混淆的情况下,dG(v),NG(v)可分别简记为d(v),N(v);对于平面图G的一个面f,用b(f)表示面f的周界,d(f)表示b(f)的边数.若d(f)=k(d(f)≥k,d(f)≤k),则称f为一个k-面(k+-面,k--面);对于平面图G的一个顶点v,若d(v)=k(d(v)≥k,d(v)≤k),则称v为一个k-点(k+-点,k--点).对于2个正整数k,r,图G的(k,r)-动态染色(简称(k,r)-染色)是指映射φ:V(G)→{1,2,…,k},满足:
1)对任意的uv∈E(G),有φ(u)≠φ(v);
2)对任意的v∈V(G),有|φ(NG(v))|≥min{dG(v),r}.
对于正整数k和r,称χr(G)=min{k|G有一个(k,r)-染色}为G的r-动态色数.
2001年,Montgomery[1]首次提出动态染色概念,并提出如下猜想:
猜想1[1]若图G是正则图,则χ2(G)≤χ(G)+2.
定理1[2]若图G是正则图,则χ2(G)≤2χ(G).
Montgomery[1]证明了猜想1对K1,3-free图是成立的,Jahanbekam等[3]证明了猜想1对直径为2的图是成立的,且Akbari等[4]证明了猜想1对k-正则二部图是成立的,其中k≥4.
Bowler等[5]构造了χ1(G)=n(n≥2)、χ2(G)=2n的正则图G,该例证明了猜想1是错误的,并且说明Alishahi[2]证明的定理1中关于2-动态色数是紧的.
对于无围长限制的部分平面图G,χr(G)的最新结果有:
定理2[6]对于任意平面图G,有χ2(G)≤5.
定理3[7]对于任意连通平面图G,除C5外,有χ2(G)≤4.
定理4[8]对于任意平面图G,有χ3(G)≤10.
定理5[9]对于r≥8的平面图G,有χr(G)≤2r+16.
文献[10-14]还证明了部分平面图χr(G)的上界,结果见表1.

表1 部分平面图χr(G)的上界
本文将证明下面的定理:
定理6平面图G是围长g(G)≥5且5-圈与5-圈不相邻的简单图,若r≥11,则χr(G)≤r+4.
1 记 号
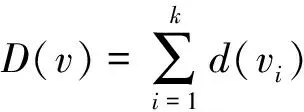
对于V′⊆V,令G[V′]为G在V′上的导出子图,若存在映射φ:V′→[k]是G[V′]上的一个(k,r)-染色,则称φ是G关于G[V′]的部分(k,r)-染色.当φ是G的部分(k,r)-染色时,对于v∈V-V′,令{φ(v)}=Ø,对于v∈V,定义如下颜色集φ[v]:

2 定理6的证明
下面利用极小反例和权转移的方法证明定理6.设图G是定理6中使得|V(G)|+|E(G)|最小的一个反例,即图G是g(G)≥5且5-圈与5-圈不相邻的平面图,r≥11,χr(G)≥r+5,但对于G中的任意一条边e,有χr(G-e)≤r+4.为了方便,记k=r+4.首先,G是连通的简单平面图.接下来探讨G的结构性质.
引理1对于平面图G,有:
1)G是2-连通的;
2)G中的2-点与2-点不相邻.
证明1)若v为G的一个割点,令G1与G2是G中满足V(G1)∩V(G2)={v}和G=G1∪G2的2个连通子图,则由G的极小性知,Gi有一个(k,r)-染色φi(i=1,2).当φ1(v)=φ2(v)时,若|φ1(NG1(v))∪φ2(NG2(v))|≥min{dG(v),r},则定义一个新的染色φ:V(G)→[k];当u∈V(Gi)时,φ(u)=φi(u)(1≤i≤2).显然,φ是G中一个(k,r)-染色.若|φ1(NG1(v))∪φ2(NG2(v))| 2)若G有2个相邻的2-点u和v,记N(u)={v,u1},N(v)={u,v1},则由G的极小性知,G′=G-uv是(k,r)-可染的.除去u,v的颜色,因为|F(u)|≤|φ[u1]∪{φ(v1)}|≤r+1 引理2轻点与轻点不相邻. 证明若G有2个相邻的轻点u和v,则由G的极小性知,G′=G-uv是(k,r)-可染的.除去u,v的颜色,因为|F(u)|≤D(u)-1≤r+2,|F(v)|≤D(v)-1≤r+2,所以u,v可以重新染好,得到G的(k,r)-染色,矛盾.引理2证毕. 引理3对于图G,有: 1)3-点v至多与1个2-点相邻; 2)轻3-点与2-点及3(1)-点不相邻; 3)3(1)-点与3(1)-点不相邻. 证明1)若v与至少2个2-点v1和v2相邻,则由G的极小性知,G′=G-vv1是(k,r)-可染的.除去v,v1的颜色,因为|F(v)|≤|φ[v3]∪{φ(v11),φ(v2),φ(v21)}|≤r+3,|F(v1)|≤|φ[v11]∪{φ(v2),φ(v3)}|≤r+2,所以v,v1可依次重新染好,得到G的(k,r)-染色,矛盾. 2)若G中的轻3-点u和2-点v相邻,记N(u)={v,u1,u2},N(v)={u,v1},d(u1)+d(u2)≤r+1,则由G的极小性知,G′=G-uv是(k,r)-可染的.除去u,v的颜色,因为|F(u)|≤|φ[u1]∪φ[u2]∪{φ(v1)}|≤d(u1)+d(u2)+1≤r+2,|F(v)|≤|φ[v1]∪{φ(u1),φ(u2)}|≤r+2,所以u,v可重新染好,得到G的(k,r)-染色,矛盾. 若G中存在轻3-点u和3(1)-点v相邻,记N(u)={v,u1,u2},N(v)={u,v1,v2},其中d(v1)=2,d(u1)+d(u2)≤r,则由G的极小性知,G′=G-vv1是(k,r)-可染的.除去v,u,v1的颜色,因为|F(v)|≤|φ[v2]∪{φ(v11),φ(u1),φ(u2)}|≤r+3,|F(u)|≤|φ[u1]∪φ[u2]∪{φ(v2)}|≤d(u1)+d(u2)+1≤r+1,|F(v1)|≤|φ[v11]∪{φ(v2)}|≤r+1,所以v,u,v1可依次重新染好,得到G的(k,r)-染色,矛盾. 3)若3(1)-点u与3(1)-点v相邻,其中N(u)={u1,u2,v},N(v)={v1,v2,u},d(u1)=d(v1)=2,N(u1)={u11,u},N(v1)={v11,v},则由G的极小性知,G′=G-uv是(k,r)-可染的.除去u,v,v1,u1的颜色,因为|F(u)|≤|φ[u2]∪{φ(u11),φ(v2)}|≤r+2,|F(v)|≤|φ[v2]∪{φ(v11),φ(u2)}|≤r+2,所以u,v可以染好.此时|F(v1)|≤|φ[v11]∪{φ(v2),φ(u),φ(v)}|≤r+3,|F(u1)|≤|φ[u11]∪{φ(u2),φ(u),φ(v)}|≤r+3.若N(u1)∩N(v1)=Ø,则u1与v1可染相同的颜色,u1,v1可以染好,故得到G的(k,r)-染色,矛盾.当u1,v1有公共邻点u11=v11时,因为|F(u1)|≤r+3,所以u1可以染好.若|φ(N(u11))|=|φ(N(v11))|≥r-1,则|φ(N(v11))|≥r,故φ[v11]={φ(v11)}.因为|F(v1)|≤|φ[v11]∪{φ(v),φ(u),φ(v2)}|≤4,所以v1可以染好,得到G的(k,r)-染色,矛盾.若u1,v1有公共邻点u11=v11且|φ(N(u11))|=|φ(N(v11))|≤r-2,则|F(v1)|≤|φ[v11]∪{φ(v2),φ(u),φ(v)}|≤r-2+3=r+1,|F(u1)|≤|φ[u11]∪{φ(u2),φ(u),φ(v)}|≤r-2+3=r+1.因此,u1,v1可以染好,得到G的(k,r)-染色,矛盾.引理3证毕. 引理4对于图G,有: 1)轻4-点与2-点不相邻; 2)4(3)-点与轻2-点不相邻. 证明1)若G中存在轻4-点v,其中N(v)={v1,v2,v3,v4},d(v1)=2,N(v1)={v,v11},则由G的极小性知,G′=G-vv1是(k,r)-可染的.由于v为轻点,故d(v2)+d(v3)+d(v4)≤r+1.除去v,v1的颜色,因为|F(v1)|≤|φ[v11]∪{φ(v2),φ(v3),φ(v4)}|≤r+3,|F(v)|≤|φ[v2]∪φ[v3]∪φ[v4]∪{φ(v11)}|≤r+2,所以v1,v可以依次重新染好,得到G的(k,r)-染色,矛盾. 2)对于4(3)-点v,记N(v)={v1,v2,v3,v4},d(vi)=2 (i=1,2,3).若v1为轻2-点,则d(v11)≤r-1.由G的极小性知,G′=G-vv1是(k,r)-可染的.现除去v,v2,v3,v1的颜色,因为|F(v)|≤|φ[v4]∪{φ(v11),φ(v21),φ(v31)}|≤r+3,|F(v2)|≤|φ[v21]∪{φ(v4)}|≤r+1,|F(v3)|≤|φ[v31]∪{φ(v4)}|≤r+1,|F(v1)|≤|φ[v11]∪{φ(v4)}|≤d(v11)+1≤r,所以v,v2,v3,v1可依次重新染好,得到G的(k,r)-染色,矛盾.引理4证毕. 引理5对于5-点v,其中N(v)={v1,v2,v3,v4,v5},d(vi)=2,N(vi)={v,vi1}(i=1,2,3,4),若d(v5)≤6,则d(vi1)≥r-1(i=1,2,3,4). 证明假设d(v11)≤r-2,由G的极小性知,G′=G-vv1是(k,r)-可染的.现除去v2,v3,v4,v,v1的颜色,因为|F(v2)|≤|φ[v21]∪{φ(v5)}|≤r+1,|F(v3)|≤|φ[v31]∪{φ(v3)}|≤r+1,|F(v4)|≤|φ[v41]∪{φ(v5)}|≤r+1,|F(v)|≤|φ[v5]∪{φ(v11),φ(v21),φ(v31),φ(v41)}|≤6+4≤r-1,|F(v1)|≤|φ[v11]∪{φ(v5)}|≤r-1,所以v2,v3,v4,v,v1可依次重新染好,得到G的(k,r)-染色,矛盾.引理5证毕. 引理6对于6-点v,其中N(v)={v1,v2,v3,v4,v5,v6},d(vi)=2,N(vi)={v,vi1}(i=1,2,3,4,5),若d(v6)≤6,则{v11,v21,v31,v41,v51}中至少有4个(r-2)+-点. 证明若{v11,v21,v31,v41,v51}中至多有3个(r-2)+-点,则{v11,v21,v31,v41,v51}中至少有2个(r-3)--点.不妨假设d(v11)≤r-3,d(v21)≤r-3.由G的极小性知,G′=G-vv1是(k,r)-可染的.现除去v3,v4,v5,v,v1,v2的颜色,因为|F(v3)|≤|φ[v31]∪{φ(v6)}|≤r+1,|F(v4)|≤|φ[v41]∪{φ(v6)}|≤r+1,|F(v5)|≤|φ[v51]∪{φ(v6)}|≤r+1,|F(v)|≤|{φ(v11),φ(v21),φ(v31),φ(v41),φ(v51)}∪φ[v6]|≤5+6≤r,|F(v1)|≤|φ[v11]∪{φ(v6)}|≤r-2,|F(v2)|≤|φ[v21]∪{φ(v6)}|≤r-2,所以v3,v4,v5,v,v1,v2可依次重新染好,得到G的(k,r)-染色,矛盾.引理6证毕. 该矛盾说明G不存在,从而定理6成立.为方便起见,用τ(S→u)表示S中元素给u转的权值总和.下面是权转移规则: 表2 d(v)≥10,5≤d(u)≤6,u与v弱相邻,同时满足条件1与2时,v给u转移的权值 2)若5≤d(u)≤6,d(v)≥10,u与v弱相邻,则当v满足下列条件之一时,称顶点v为a-点: ①n2(v)=d(v)-1且W(v)与N(v)中9+-点的个数均大于等于1; ②d(v)-4≤n2(v)≤d(v)-2且N(v)中9+-点的个数大于等于1; ③n2(v)≤d(v)-5. 3)若5≤d(u)≤6,d(v)≥10,u与v弱相邻,则当v满足下列条件之一时,称顶点v为c-点: ①n2(v)=d(v)且W(v)中9+-点的个数大于等于2; ②n2(v)=d(v)-1且W(v)中9+-点的个数大于等于1,N(v)中无9+-点; ③d(v)-4≤n2(v)≤d(v)-2且N(v)中无9+-点. 1)d(v)=2,ω(v)=-2,记f1和f2为与v关联的面. 3)d(v)=4,ω(v)=1.由引理4中1)知,n2(v)≤3. ①n2(v)=5.v为轻点,由引理2知,vi为重点,故d(vi1)≥r+4-5=r-1≥10(1≤i≤5).记f1,f2,f3,f4,f5为与v关联的面. 5)d(v)=6,ω(v)=4. 7)d(v)=8,ω(v)=7. 综上,得到了下面有矛盾的式子: 上面的矛盾说明G不存在,从而定理6是成立的. 本文在前人研究的基础上,对平面图的限制条件进行了调整,进而得到了更好的上界.平面图在不同的限制条件下还有很多有意义的性质,因此,可以在这些性质下进一步研究平面图的r-动态色数,并得到一些更有意义的结果.
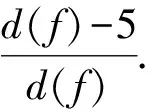
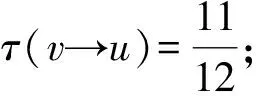
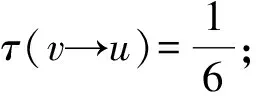
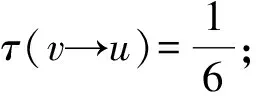

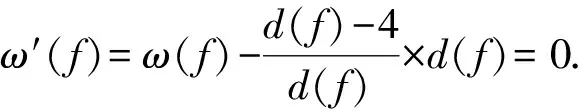
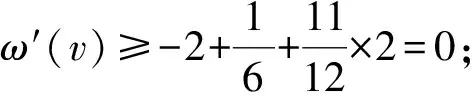
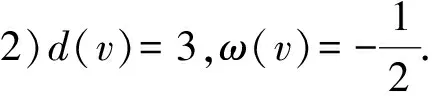
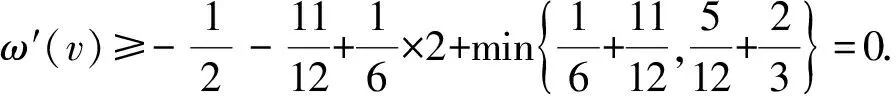
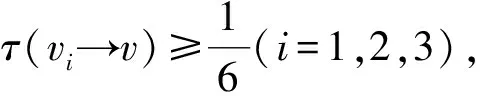
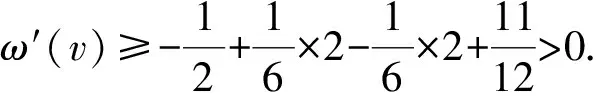
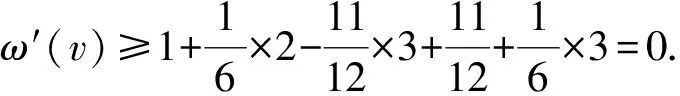
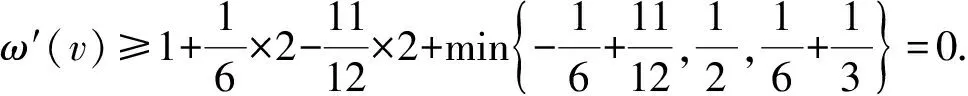
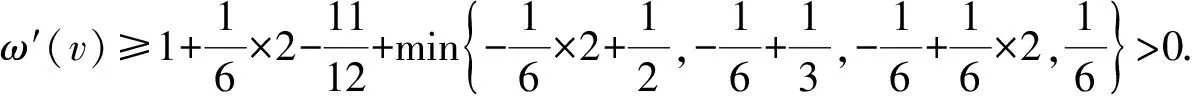
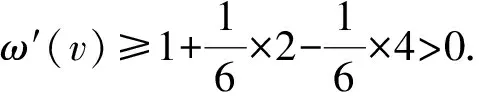
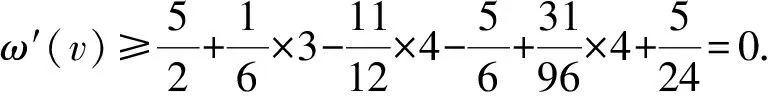
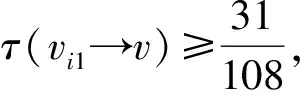

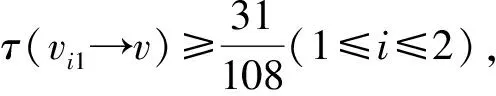
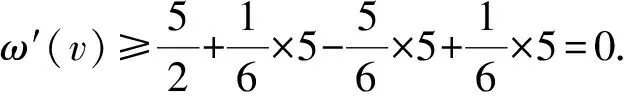
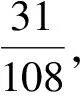
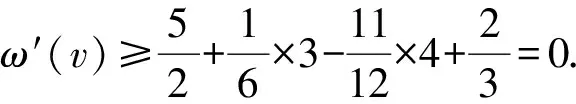
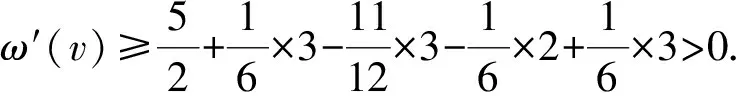
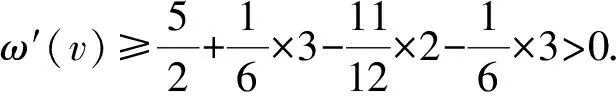
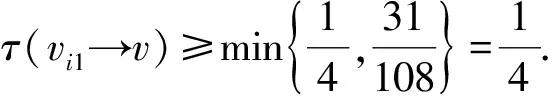
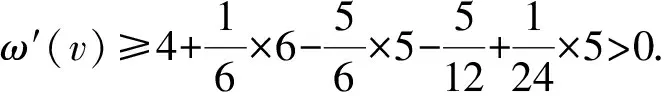
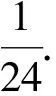
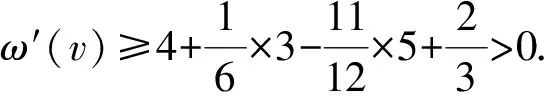
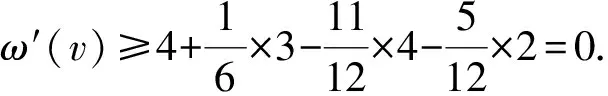
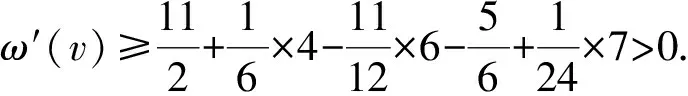
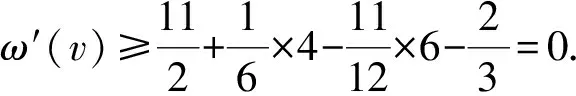
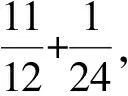
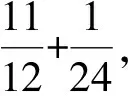
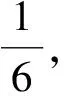
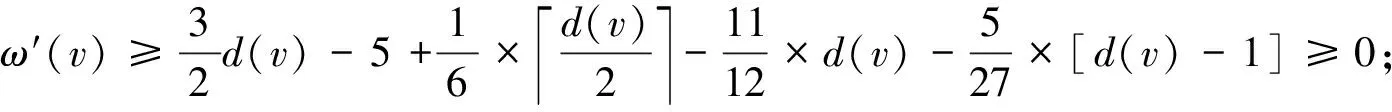
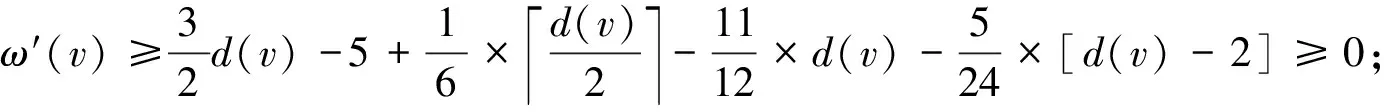
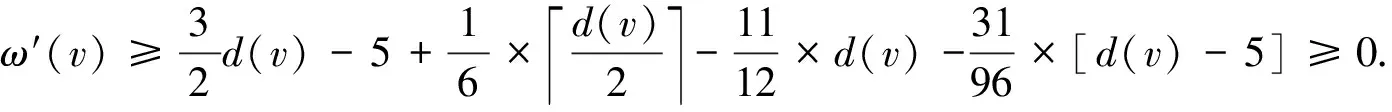
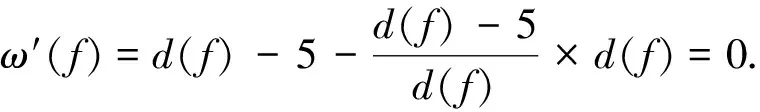
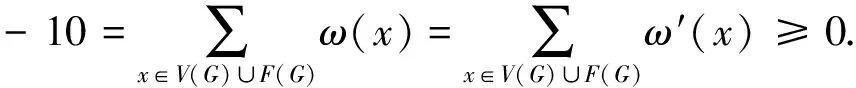
3 结 语

