浅谈电动力学角域静电场问题
石寰宇,苗荣欣
(中山大学 物理与天文学院,广东 珠海 519082)
电动力学教学中会涉及求解角域的静电场问题,这类问题可以利用镜像法、分离变量法和格林函数法等多种方法求解,有助于学生对比各种方法的异同和优缺点,加深对静电场问题的理解.然而这类问题的求解对本科生而言并不简单,需要一定的技巧和较强的数学物理基础.本文详细给出角域静电场问题的求解,可以很好地辅助电动力学教学和本科生自学电动力学.此外相关结果可以用来求解角域的卡西米尔效应,具有一定的现实意义.
角域静电场问题是指:两块相交的半无限大接地导体板内有电荷分布,形成的角域夹角大小为α,求解角域内任一点的电势或电场.文献[1]讨论了源电荷为无限长均匀带电的线电荷时,任意夹角的角域问题,并通过保角变换法给出通解.文献[2-4]讨论了源电荷为点电荷时的几种特殊夹角下的角域问题,并通过电像法给出了电势.文献[5,6]则证明了当且仅当α=π/n(n=1,2,3,…)时,电像法才适用.文献[7]给出了任意夹角的结果,但没有严格证明α=π/n时解可以退化至电像法给出的结果,也没有讨论第二类边界条件和混合边界条件的情况.
本文讨论了角域内源电荷为点电荷的情况,通过电像法给出了α=π/n时的电势分布,进一步通过分离变量法给出了任意角度α时的电势分布,通过数学计算严格证明了两种方法所得到的解在α=π/n时是等价的,并对两结果辅以Mathematica进行讨论和验证,且通过等势图的绘制说明了级数解具有较好的收敛性.最后将此问题拓展到第二类边值问题及混合边值问题,并给出相应的电势通解.本文还得到一系列关于第二类勒让德函数Qν(x)的恒等式,这在一般的数学手册中是没有的,它们在处理一些具有轴对称性的边值问题时能发挥重要作用.需要指出的是,由角域点电荷产生的电势可以得到格林函数,从而求解最一般的角域静电场问题.因此本文实际上研究了最一般的情况而不仅仅是点电荷.
1 角域静电场问题模型
1.1 问题重述
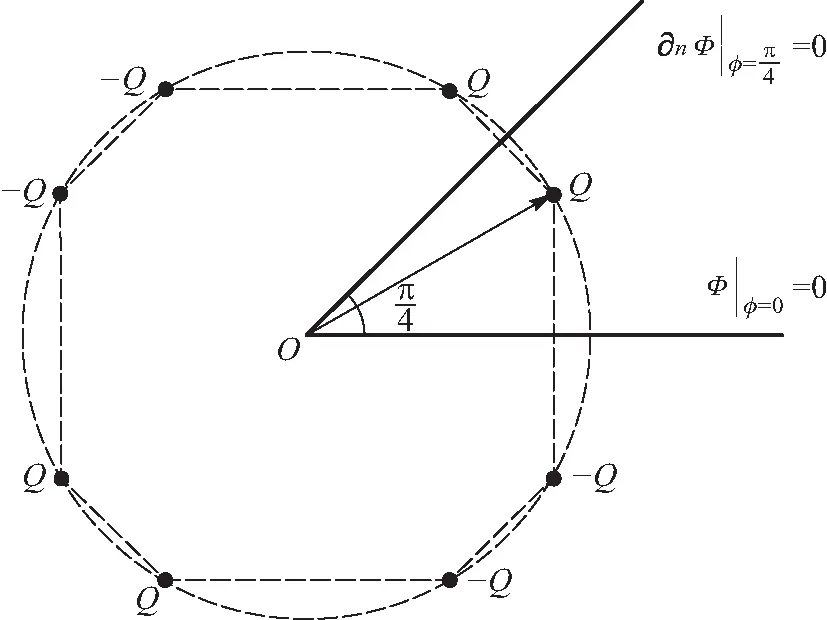
如图1所示,两块接地的半无限大导体板在一侧相交且夹角为α,在其形成的角域内有一个点电荷Q.建立柱坐标系,z方向垂直纸面朝外,r-φ平面设在源电荷所在平面,坐标原点选为两平面相交处,且源电荷的位置在(r0,φ0,0)处.试求角域内任意一点的电势大小.
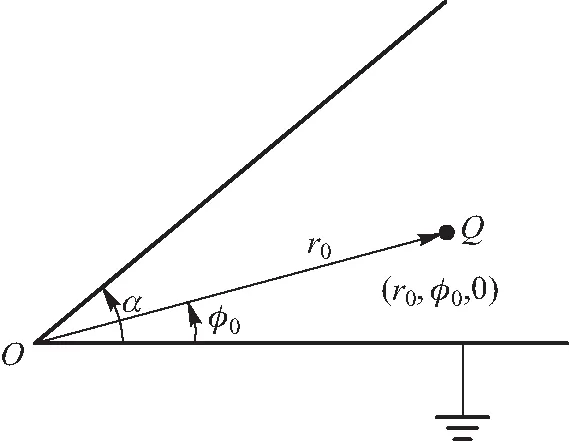
图1 角域静电场问题图示
1.2 问题分析
由于角域内点电荷的存在,会使得导体板表面产生感应电荷.感应电荷和源电荷共同作用使得导体板上的电势维持在零电势.只要能够求出感应电荷分布,便能求出角域内任意位置的电势.但感应电荷分布往往颇为复杂,它不仅和角域夹角大小α有关,还与源电荷的具体位置有关.在一些对称性较高的条件下,我们可以通过电像法在角域外构造像电荷来解决此问题,但对于一般情况需要我们求解含第一类边界条件的泊松方程.接下来我们先讨论α=π/n的情况,再将此结果推广至任意的夹角α.
1.3 电像法
依据电像法[8],我们可以在角域外构造适当的点电荷使得导体边界上的电势为零电势.其中源电荷Q位于角域内,其余的像电荷全部位于角域外以保证泊松方程的源不变.在所有电荷的共同作用下,两导体板的电势保持为零电势从而不改变原问题的边界条件.如图2所示,我们列举了n=2,3,4时的三类情况以作说明.从中我们可以总结出以下几点规律:1) 所有电荷(源电荷+像电荷)的总数目为2n个;2) 源电荷与像电荷围成的图形是圆内接2n边形,且圆心为角域顶点,圆的半径为源电荷到坐标原点的距离r0;3) 随着极角φ的增加,点电荷的电性按照正、负交错排列,每个电荷的电荷量大小均为Q.
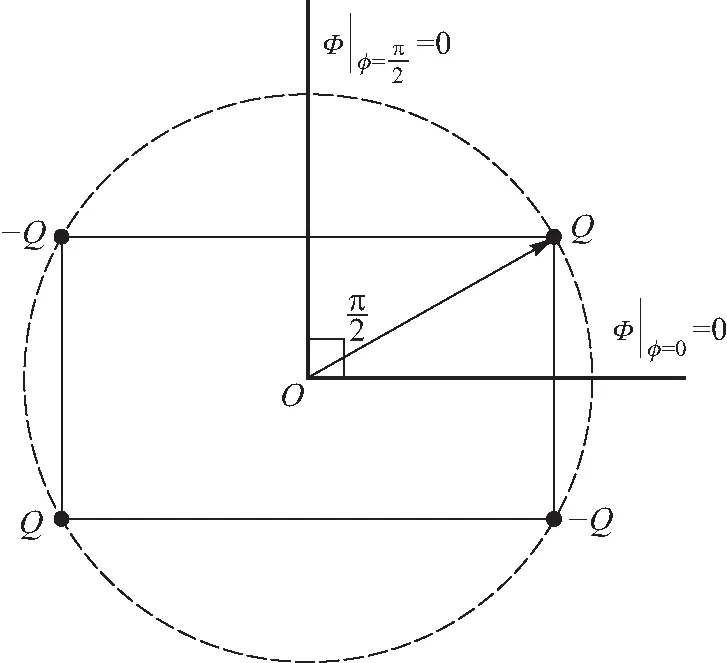
(a) α=π/2的情形
对于一般的α=π/n,通过简单的几何关系,我们可以确定所有电荷的角位置:
(1)
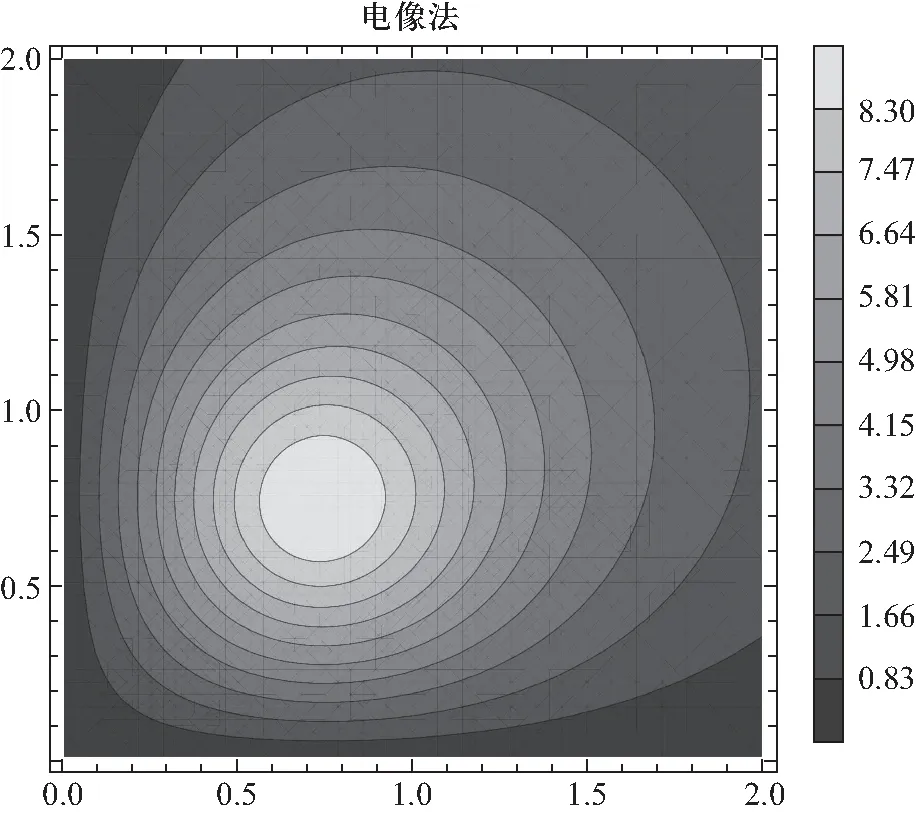
其中i=1代表的是源电荷的角位置,其余为像电荷的角位置.那么角域内{Ω(r,φ,z)|r>0,0<φ<α,-∞ (2) 其中φi由(1)给出.特别地,当 (3) 这意味着源电荷位于角域的角平分线处,源电荷与像电荷围成了圆内正接2n边形,体系有较高的对称性,此时的φi则可表为: (4) 上述讨论局限于α=π/n,对于更一般的情况,即α任意,此时电像法不再适用(像电荷最终会出现在角域内部,这改变了原有的泊松方程的源,不符合唯一性定理的要求),此时最为直接的方法便是通过分离变量法解含第一类边界条件的泊松方程. 分离变量法是求解定解问题的一种基本方法,其基本思想是将复杂的偏微分方程分解为几个可以求解的常微分方程,带有边界条件的常微分方程构成了本征值问题.对于含源的定解问题一般求解思路是将源分解为本征函数的线性组合,本文提供另一种角度:充分利用正交函数族的正交性质来确定源[9]. 考虑α任意的情况,在圆柱坐标系中,原边值问题作为一个定解问题可以表示为: (5) 考虑解是可以分离变量的[10],即 Φ(r,φ,z)=R(r)ψ(φ)Z(z) (6) 在r≠r0时,(5)转变为拉普拉斯方程,经过适当变形得 (7) 上式右边是φ的函数,左边是r、z的函数,两边只能是同一个常数,记为m2.再考虑到边界条件,即导体板上的电势为0,为满足此边界条件只能有 (8) 另一方面,考虑r、z方向,则有 (9) 同样地,上式右边是z的函数,左边是r的函数,显然两边只能是同一个常数.可规定μ>0,考虑到原问题关于z=0平面对称,则本征函数只能有 Z(z)=cos(μz), (μ连续,μ>0) (10) 最后对于r方向,R(r)满足方程是: (11) 这是m阶虚宗量贝塞尔方程,它的解为 R(r)=AIm(μr)+BKm(μr) (12) 其中Im(x)和Km(x)分别是第一类和第二类虚宗量贝塞尔函数.由两类虚宗量贝塞尔函数在r→0及r→∞的行为,要保证所求电势在角域内连续且不发散,R(r)需分为两个区域: (13) 整合(8),(10),(13)得定解问题的本征函数: (14) 那么通解则是对应本征函数的线性组合: (15) 为解得通解中的系数Akμ、Bkμ的具体表达式,我们还需要找出它们满足的两个关系式。利用电势在r=r0处连续的条件,我们可以得到: (16) 利用下述两个关系式进行化简[11]: (17) 可得到系数Akμ、Bkμ满足的第1个关系式: AkμIkπ/α(μr0)=BkμKkπ/α(μr0) (18) 其次考虑到泊松方程的源为狄拉克函数,利用r方向的本征函数R(r)在r=r0处的导数不连续,将(15)代入式(5)中,并对r0的邻域做积分可以得到下述关系式: (19) 同样利用(17)中的两个关系式,可将式(19)化简为系数Akμ、Bkμ满足的第2个关系式: (20) 由两类虚宗量贝塞尔函数的朗斯基行列式满足的阿贝尔性质[12]: (21) 联立式(18)、(20),并在化简中利用式(21)便可解得系数Akμ、Bkμ: (22) 将(22)式代入式(15)式中,同时可将通解整合为更加紧凑的形式: Φ(r,φ,z)= (23) 其中r<=min{r0,r},r>=max{r0,r}.上述积分还可以做进一步化简,文献[12]给出了下述公式: (24) Φ(r,φ,z)= (25) 角域{Ω(r,φ,z)|r>0,0<φ<α,-∞ 在第1节中我们分别应用电像法及分离变量法求得式(2)及式(25)两类电势通解.当α=π/n时,式(25)和式(2)描述的是同一类边值问题的解,依据唯一性定理它们应当是等价的,我们可以从数学角度严格证明式(25)可以退化至式(2). 事实上式(25)即为第一类边界条件的角域格林函数.而仿照1.4节的过程,我们可以推导出自由空间中格林函数在柱坐标下的一般展开式[13]: (26) 利用式(26)将式(2)展开,同时利用式(24)进行化简可得 (27) 考虑α=π/n,并将式(27)代入式(2)中整合进行化简得到 (28) 这便是我们要验证的等式,我们通过数学推导确切地证明了当α=π/n时,式(25)能够退化至式(2).特别地,当φ0=α/2时,式(28)可转变为 (29) 其中φk由式(1)和式(4)式给出. 下面通过Mathematica针对式(2)及式(25)绘制了α=π/2,φ0=π/4,r0=1情况下的等势线通过2种方法的数值计算结果比较可知这两个表达式所得结果彼此吻合.其中图3(b)选取式(25)求和为前20项,最终与电像法所得结果的误差仅为10-11量级,可以定性判断级数收敛非常快且计算精度较高.另外从图3(c)中可知误差主要集中于源电荷附近,这是由于源电荷处电势发散,在其附近的数值计算精度较低带来了较大的误差. (a) 电像法 在前述讨论中我们已经顺利解决了两导体板接地时的角域静电场问题并通过电像法以及分离变量法给出了通解,由此自然联想到对于其他边界条件是否可以通过类似的办法解决相应的角域静电场问题.通过分析,我们发现电像法和分离变量法依然适用,但处理过程存在一定差异. 参考图1,将两板所满足的边界条件更改为电势的法向导数为零.该第二类边界条件的定解问题可以表述为: (30) 在α=π/n时,电像法依然成立,图4给出了n=4时的像电荷示意.与第一类边值问题不同,此时所有的像电荷电性与源电荷一致,但像电荷的角位置φi依然可以由式(1)给出.那么角域内任意一点的电势则可表示为 (31) 图4 n=4时的第二类边值问题电像法 对于任意夹角α的情况,利用分离变量法仿照1.4节可以得到角域内电势分布为 (32) 仿照2.1节同样可以验证式(32)在α=π/n退化至式(31),由此又可得到关于第二类勒让德函数Qν(x)的恒等式: (33) 参考图1,此时将φ=0处的平板接地,φ=α处的平板电势法向导数保持为零.该混合边界条件的定解问题可以表述为 (34) 混合边值问题与前述两类边值问题有所不同,电像法仅在α=π/2n时适用(在α=π/n时像电荷的电性会出现矛盾),此时的电荷可按照(正、正、负、负)归为一组,角域电势由4n个电荷共同作用,每一个电荷的角位置φi应由式(1)修正为 (35) 那么角域空间的电势可以表示为 (36) 图5 n=2时的混合边值问题电像法 同样利用分离变量法可给出任意夹角α时的电势分布: (37) 在α=π/2n时式(37)可退化至式(36),又可得到关于第二类勒让德函数新的恒等式: sin[(2k-1)nφ0]sin[(2k-1)nφ] (38) 本文通过电像法和分离变量法解决了三类边界条件下的角域静电场问题,并给出了角域内部的电势解析表达式.电像法仅适用于对称性较高的问题,而分离变量法可以讨论任意夹角下的角域问题.对于不同种类的问题应采取不同的解决方法,这对于加深学生对静电学的理解以及帮助教师授课都有积极意义. 由格林函数的物理意义,即单位点电荷产生的电势,式(25)、式(37)、式(42)实际上对应着三类不同边界条件下的角域格林函数.一旦确定格林函数,那么便可以求解内部含复杂电荷分布的角域静电场问题.本文中的讨论便可推广到任意电荷分布情况下的角域问题. 在验证分离变量法所给电势解可以退化至电像法给出的电势解时,我们得到式(28)、(29)、(33)、(38).它们都是关于第二类勒让德函数Qν(x)的恒等式,这些结果在一般的数学手册中是没有给出的.在处理具有柱对称性的边值问题,这些恒等式都可以发挥重要的作用.1.4 分离变量法
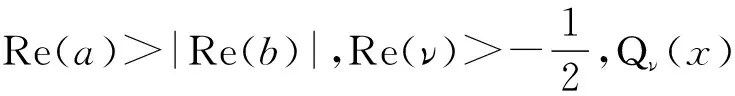
2 解的分析
2.1 数学验证
2.2 电势分布
3 其他边界条件
3.1 第二类边界条件角域问题

3.2 混合边界条件角域问题
4 总结

