立体几何中一类翻折问题的处理方法

程春民

(江西省永丰中学)

把一个平面图形沿某条直线翻折,转化为空间图形,进而研究图形在位置关系和数量关系上的变化,这就是翻折问题.高考中经常以图形翻折作为命题对象,处理这类问题的关键在于弄清楚哪些量发生了变化,哪些量未发生变化.本文通过具体例子说明处理这类翻折问题的基本方法.

例1如图1 所示,四边形ABCD是菱形,∠BCD＝60°,AB＝2.沿BD把△ABD折起,使点A翻折到点P的位置,连接PC,则四面体P-BCD(如图2)的体积的最大值是________.

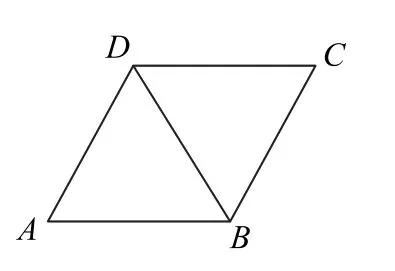
图1

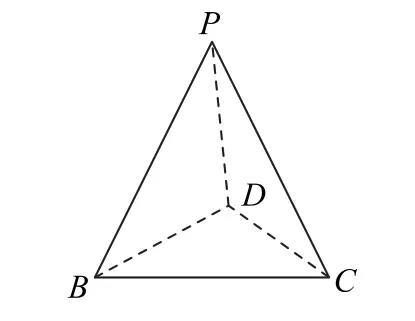
图2

解析如图3 所示,当平面PBD⊥平面BCD时,四面体P-BCD的体积最大,过点P作PE⊥BD于点E,则V＝

图3

例2点D是Rt△ABC斜边AB上一动点,AC＝3,BC＝4,将△BCD沿着CD翻折,翻折后的三角形为△B′CD,且平面B′CD⊥平面ADC,则翻折后AB′的最小值是( ).

图4

因为平面B′CD⊥平面ACD,B′E⊥CD,所以B′E⊥平面ACD,故B′E⊥AE.在Rt△AEB′中,由勾股定理得AB′2＝AE2＋B′E2＝25－12sin2α.当时,AB′取得最小值,故选B.

例3如图5所示,已知四面体ABCD中,AD＝DB＝AC＝CB＝1,则该四面体体积的最大值为________.

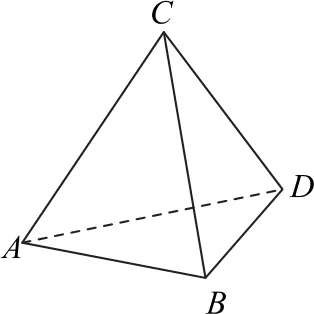
图5

解析当此四面体体积最大时,平面ABC⊥ABD,取AB中点M,连接CM,DM(如图6),则CM⊥平面ABD.设AB＝2x(0＜x＜1),则,所以

图6

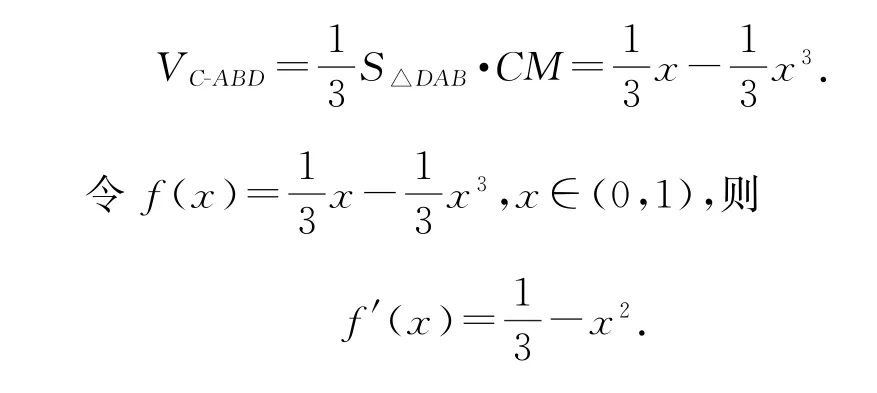
例4如图7所示,在长方形ABCD中,AB＝2,BC＝1,E为DC的中点,F为线段EC(端点除外)上的一动点,现将△ADF沿AF折起,使平面ABD⊥平面ABC,在平面ABD内过点D作DK⊥AB,K为垂足,设AK＝t,则t的取值范围是_________.

图7

解析如图8 所示,过点D作DH⊥AF,垂足为H,连接HK,因为DK⊥AB,所以AF⊥平面DHK.

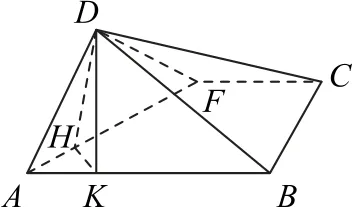
图8

在平面图形ABCD中(如图9),D,H,K三点共线,且DK⊥AF,所 以△AKD≌△DAF,则,所以.又DF∈(1,2),所以

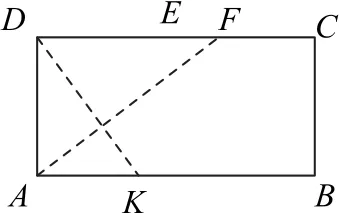
图9

例5如图10 所示,在△ABC中,AB＝BC＝2,∠ABC＝120°.若平面ABC外的点P和线段AC上的点D,满足PD＝DA,PB＝BA,则四面体P-BCD的体积最大值是_________.

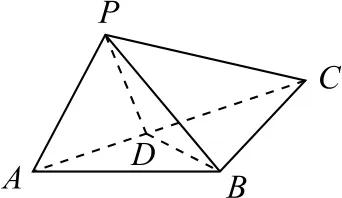
图10

解析在△ABC中,由余弦定理得

AC2＝BA2＋BC2－2BA·BCcos∠ABC＝12,所以AC＝2.当平面PBD⊥平面CDB时,四面体P-BCD的体积取得最大值.此时△PBD底边BD的高就是三棱锥VP-BCD的高.

链接练习

1.已知边长为2的等边△ABC,D为BC的中点,以AD为折痕进行折叠,使折后的∠BDC＝,则过A,B,C,D四点的球的表面积为( ).

A.3π B.4π C.5π D.6π

2.如图11所示,在正方形SG1G2G3中,E,F分别是G1G2,G2G3的中点,D是EF的中点,现在沿SE,SF及EF把这个正方形折成一个四面体,使G1,G2,G3三点重合,重合后的点记为G,则在四面体S-EFG中必有( ).

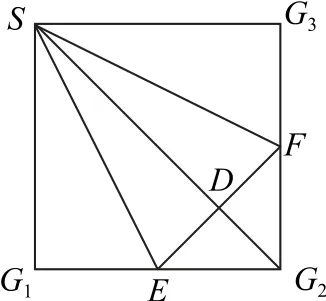
图11

链接练习参考答案

1.C. 2.A. 3.C. 4.CD.

(完)