COMPLETE MONOTONICITY FOR A NEW RATIO OF FINITELY MANY GAMMA FUNCTIONS*

Feng QI (祁锋)

Institute of Mathematics,Henan Polytechnic University，Jiaozuo 454010，ChinaSchool of Mathematical Sciences，Tiangong University，Tianjin 300387，ChinaE-mail: qifeng618@yeah.net;qifen618@gmail.com; qifeng618@hotmail.com

In [17, Theorem 2.1] and [34, Theorem 4.1], the functions

2 A Lemma

For stating and proving our main results, we need a lemma below.

Lemma 2.1 Let

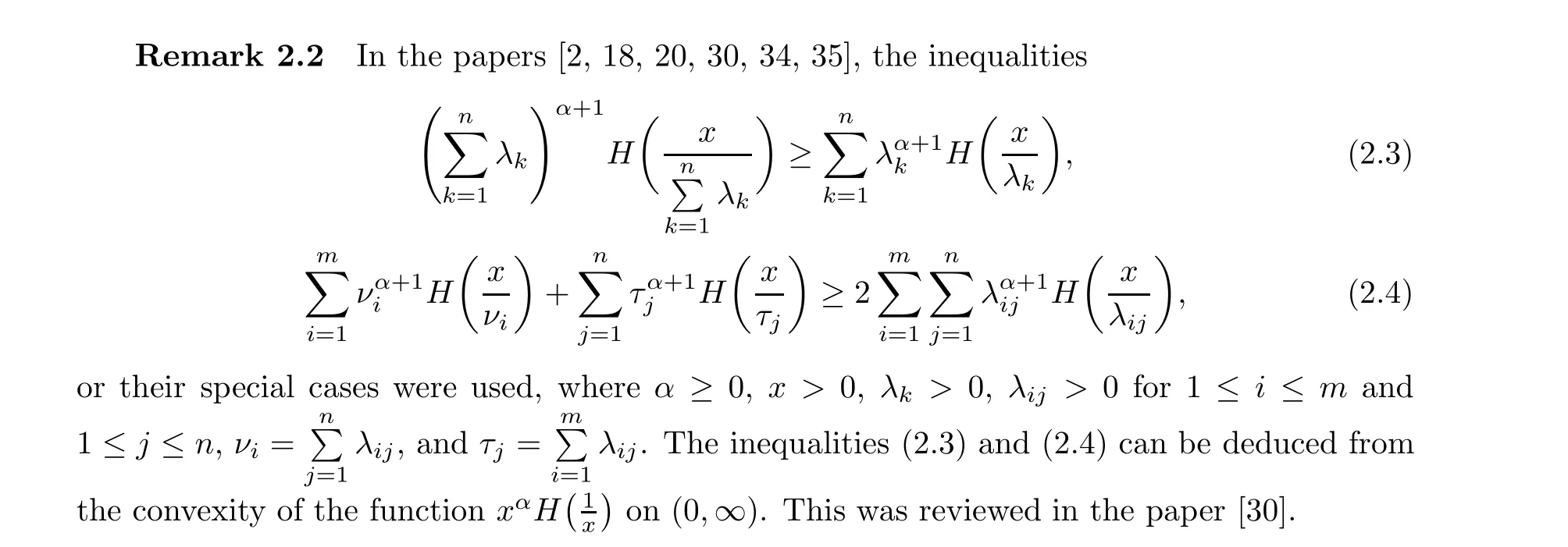
3 Complete Monotonicity

4. for all ρ ≥1 and θ ≥0, the second derivative [ln Fρ,θ(x)]＇＇is a completely monotonic function on (0,∞).

Proof Taking the logarithm on both sides of (1.8) and computing give

By virtue of inequality (2.1), we derive readily that, when ρ ≥1 and θ ≥0, the second derivative [ln Fρ,θ(x)]＇＇is completely monotonic on (0,∞). Hence, the first derivative [ln Fρ,θ(x)]＇is increasing on (0,∞).

When ρ=1 and θ =0, it is easy to see that

4 A Simple Review

In this section, we simply review complete monotonicity of several linear combinations of finitely many digamma or trigamma functions.

Let

is a completely monotonic function on (0,∞), where q ∈(0,1), ψq(x) is the q-analogue of the digamma function ψ(x), and λk> 0 for 1 ≤k ≤n. The function in (4.2) is the q-analogue of the one in (4.1).

From the proof of [34, Theorem 4.1], we can conclude that the linear combination

From the proof of [30, Theorem 5.1], we can conclude that if ρ ≤2 and θ ≥0, then the linear combination

5 Remarks

In this section, we mainly mention some conclusions of the paper [51], which was brought to the author’s attention by an anonymous referee.

Remark 5.1 It is well known that the Bernoulli numbers Bncan be generated by

which has a unique minimum and is logarithmically convex on (0,∞). This implies that the introduction of the parameter ρ in the function Fρ,θ(x) is significant and is not trivial.

Remark 5.3This paper is a revised version of the electronic preprint [23], and a companion of the series of papers [18, 20, 30, 34, 35, 40] and the references therein.

AcknowledgementsThe author thanks the anonymous referees for their careful corrections to, valuable comments on, and helpful suggestions regarding the original version of this paper.