IMPULSIVE EXPONENTIAL SYNCHRONIZATIONOF FRACTIONAL-ORDER COMPLEX DYNAMICALNETWORKS WITH DERIVATIVE COUPLINGS VIAFEEDBACK CONTROL BASED ON DISCRETE TIME STATE OBSERVATIONS*
Ruihong LI (李瑞鸿)Huaiqin WU(武怀勤)*
School of Science,Yanshan University,Qinhuangdao 066001,China E-mail : ruihongli2020@163.com; huaiqinwu@gysu.edu.cn
Jinde CAO(曹进德)
School of Mathematics,Southeast Uniuersity,Nanjing 210096,China Yonsei Frontier Lab,Yonsei University,Seoul 03722, Korea E-mail : jdcao@seu.edu.cn
Many practical systems are often suddenly impacted by external instantaneous disturbance,which makes the state of system abruptly change at a discrete time. This phenomenon can be described by impulse effects. Because impulsive effects are significant for understanding the dynamical behaviors of most real-world complex networks, some researchers have incorporated impulsive effects into CDNs [11-14]. In [11], global power synchronization conditions were acquired by introducing the concept of a log average impulsive interval for impulsive CDNs with a proportional delay. Yogambigai et al. [13] investigated impulsive synchronization for Markovian jumping CDNs with hybrid coupling by utilizing a pinning control. A novel lemma was presented in [14] to ensure the synchronization in fixed-time of impulsive CDNs.
Furthermore,many practical networks,such as communication networks,signal processing,etc, can be modeled via multiple weighted CDNs; for some relevant studies, see [15-18]. A novel hybrid controller was designed in [16] to obtain the fixed time stochastic synchronization conditions for semi-Markov switching CDNs with multiple weights. In[18], Jia et al. addressed the global robust finite-time synchronization for FCDNs under asynchronous switching topology by using a non-fragile controller.
As we know, the coupling term describes the relationship between a given state and other states. Until now, the main coupling forms have modeled, such as nonlinear coupling [19],intermittent coupling [20], derivative coupling [21], and so on. General state coupling represents the systems coupled at time t, which describes the spatial position of the current system,while derivative coupling denotes the current subsystem state and the derivative state of the other subsystems coupled at a given time, which is regarded as the velocity of information transmission among different subsystems. For example, Tang et al. [22] discussed the exponential synchronization for delay neural networks with derivative couplings and cluster-tree directed topology by applying an impulsive pinning control strategy. Reference [23] considered the finite time passivity and synchronization for CDNs with derivative couplings. Meanwhile,[26] concentrated on the exponential synchronization for CDNs with derivative couplings and a proportional delay. However, in the above results [21-26], the derivative couplings are only considered in integer-order systems. Because the characteristics and advantages of fractional calculus, it is worth introducing derivative couplings into FCDNs.
On the other hand, in many papers, coupling patterns are active at all times, which causes a great quantity of waste. If coupling among CDNs occurs at discrete moments, the problems mentioned above can be effectively avoided. In [27], the authors researched exponential synchronization of nonidentical neural networks with leakage delays and parametric uncertainties by employing an impulsive couplings controller. In [28], the synchronization of complex networks with disconnected topology was investigated via an impulsive couplings controller. Yang et al. [29] applied an impulsive couplings controller and discussed the global synchronization of multiple recurrent neural networks with time delays.
Due to the actual situation, very few complex networks can achieve synchronization by adjusting system parameters. Therefore, suitable control strategies have been proposed to synchronize the CDNs while the number of parameters are large and the CDNs structure is more complex. Over the last several decades, some control methods were proposed [32-36].Feedback control, which is a conventional control scheme, is directly adopted or combined with other control methods. Commonly, feedback control always assumes that the observation of states are continuous,but this may be impractical and costly. Consequently,Mao[37]proposed a feedback control based on discrete time state observations(FCDSO), in which the states are only observed in discrete time. In view of this improvement in feedback control,in[38],authors specified mean-square asymptotic stability conditions for multi-group models with multiple dispersal via the designed FCDSO. Xu et al. [39]established the synchronization criterion with regard to multi-link impulsive FCDNs by equipping FCDSO. The work [40] was dedicated to solving the synchronization issue for stochastic coupled systems with time-varying coupling via FCDSO. To the best of our knowledge, there have been no studies of the synchronization of FCDNs with derivative couplings and impulsive couplings via FCDSO.
With the motivations stated above, this article focuses on the global exponential synchronization of FCDNs with derivative couplings and impulse effects via FCDSO. The main contributions and novelties of this paper are highlighted as follows:
(1)Global exponential synchronization is first considered for FCDNs with a multi-fractional derivative and multi-impulsive coupling by applying FCDSO.
(2) A key lemma (Lemma 5) is developed.
(3) A new FCDSO is designed in order to achieve the synchronization objective.
(4) The global exponential synchronization conditions are derived in term of LMIs.
The rest of this article is organized as follows: in Section 2, we give some basic definitions and lemmas. In Section 3, the model of FCDNs with derivative couplings and linear impulses is presented, meanwhile, the corresponding controller is designed. In Section 4, a key lemma and exponential synchronization criterion with regard to FCDNs with derivative couplings and impulse effects are proposed. Section 5 gives two simulink examples to verify the effectiveness of the main results. Finally, a conclusion is provided in Section 6.

Table 1 Notations
2 Preliminaries
In this section, some basic definitions and lemmas are given.
Definition 2.1 ([41]) The Caputo fractional order derivative of f(t)∈Cn([0,+∞),R)is defined as

where Nζ(t0,t) represents the number of impulsive times ζ.

Remark 2.10 According to the definition of G, it is obvious that G is a symmetry seminegative definite matrix. Meanwhile, Ψ is a positive definite matrix. Then the matrix ((INnd(G⊗Ψ))is a positive definite matrix and λmin(INn-d(G⊗Ψ))=1,λmax(INn-d(B⊗Ψ))≥1.

where φi> 0 is a controller gain, and Υ(t) = [tσ]σ ([·] is an integer-valued function) denotes the duration between two continuous observations.
Remark 2.12 It is worth noting that, while σ →0, the designed discrete controller(2.3)will degenerate into a continuous feedback controller.
Let the state error be ei(t)=xi(t)-s(t), the error dynamical system can be described by
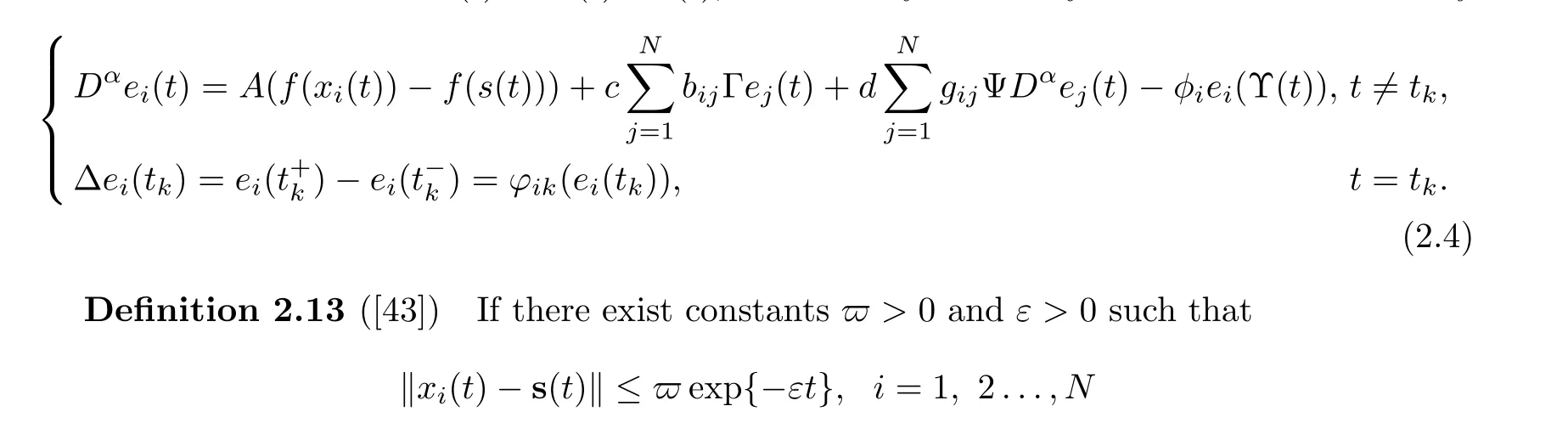
holds, then systems (2.1) and (2.2) are said to be exponentially synchronized.
Furthermore, the compact forms of (2.4) can be expressed as
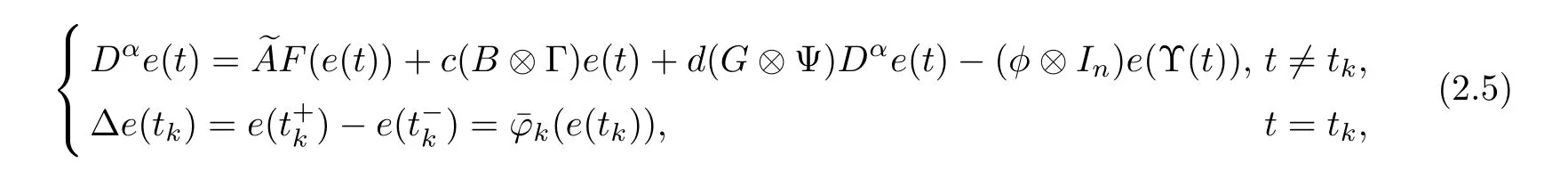
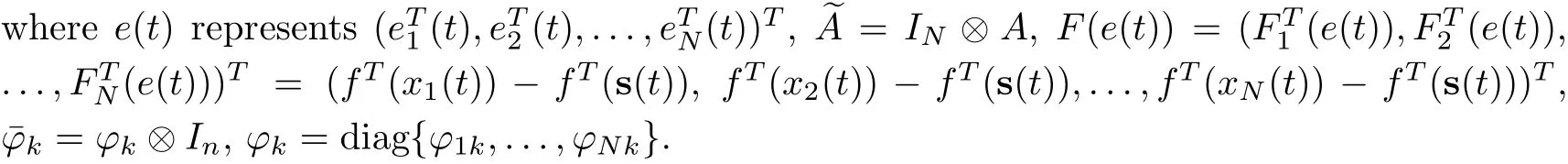
3 Main Results
3.1 Synchronization of FCDNs with derivative couplings and linear impulses
In this subsection,the exponential synchronization conditions are proposed for FCDNs with derivative couplings and linear impulses under feedback control based on discreet time state observations. To do this, we develop a useful lemma to establish the relationship between a discrete time observation term and a continuous term.


The proof is complete. □
Theorem 3.2 Under Assumption 2.1,if there exist matrix φ>0,and constant ω >0 such that the inequalities


3.2 Synchronization of FCDNs with multi-derivative couplings and impulsive couplings
In this subsection,global exponential synchronization is investigated for FCDNs with multiderivative couplings and impulsive couplings, and the sufficient condition is presented in the form of LMIs.
Consider FCDNs with multi-derivative couplings and impulsive couplings, whose dynamics are described by
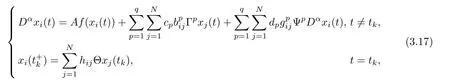


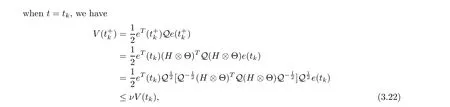

Remark 3.5 Due to the complexity of the actual situation, it is not enough to present state coupling only at all times. Derivative couplings and impulsive couplings should also be considered. Relevant studies were obtained with regard to CDNs with derivative couplings and impulsive couplings in [21-26] and [27-31], however, the above theoretical results focused on integer-order systems. In this paper,we introduce derivative couplings and impulsive couplings into FCDNs, and this makes the model of FCDNs more general.
Remark 3.6 The feedback control approach based on continuous time state observations was adopted in the synchronization research on CDNs; see [47]. To reduce costs and save resources, a feedback control strategy based on discrete time observation was proposed to study the synchronization problem for complex systems [37-40]. Inspired by [39], in Theorems 1 and 2, we investigated the impulsive exponential synchronization for FCDNs with derivative couplings via FCDSO. The results obtained are meaningful and valuable.
Remark 3.7 Owing to the fact that the feedback controller (3) is discrete, in the proof of Lemma 5, addressing the discrete items is challenging work. Analogous to [39], Lemma 5 establishes the relationship between the discrete time observations term e(Υ(t)) and the continuous term e(t). Hence, the designed discrete controller (3) is more effective.
4 Simulation Results
In this section, the theoretical analysis is illustrated by two simulation examples.
Example 4.1 Consider the FCDNs with derivative couplings and impulse effects including three nodes. When t/=tk, the corresponding parameters are as follows:

Figure 1 indicates that the dynamical system cannot achieve synchronization without a controller. To achieve global exponential synchronization,we establish the following parameters:Ta=3.125,σ =0.001,ω=0.15,τ =1,and a control gain matrix φ=[7.5,0,0;0,9.5,0;0,0,8.4].For these parameters,it is easy to verify that conditions(i)and(iii)are satisfied. The graph of synchronization errors is presented in Figure 2. It is shown that the curves of error e(t) reach zero; that is, the error system(2.4)achieves global exponential synchronization under feedback control based on discrete time state observations. Therefore, the correctness of Theorem 3.2 is verified by these simulation results.
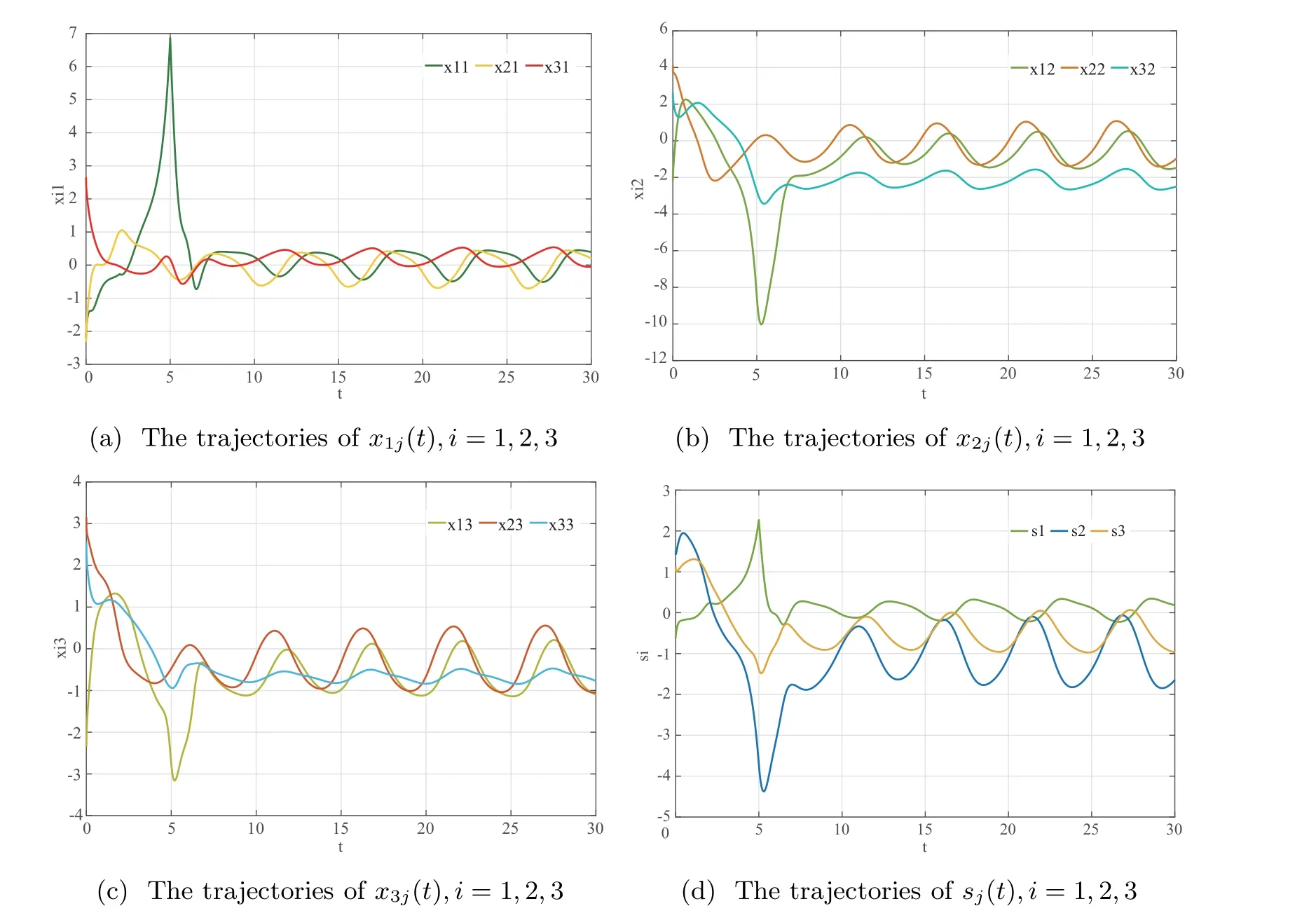
Figure 1 The trajectories of state x(t) and s(t),i,j =1,2,3; without controller
Example 4.2 FCDNs with multiple derivatives and impulsive couplings containing 3 nodes are shown by
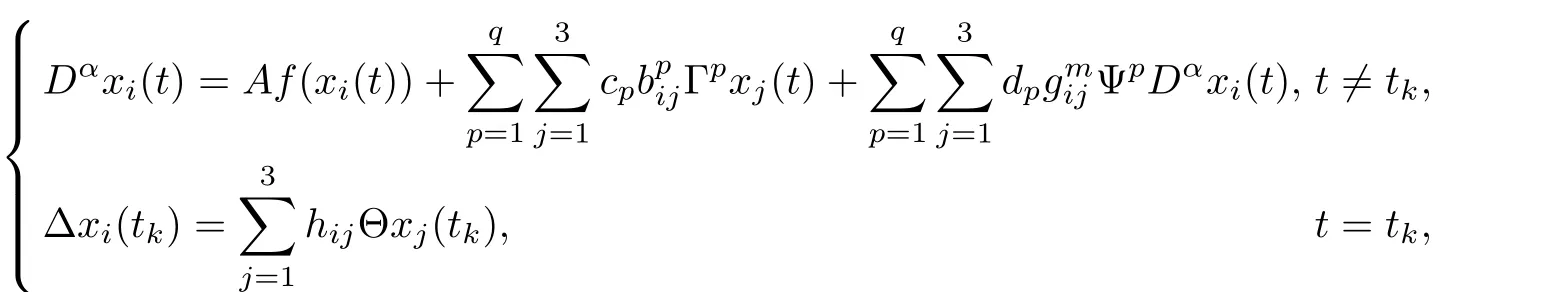
where α=0.97, q =2, c1=0.012,c2=0.03,d1=.25,d2=0.84 and f(xi1(t))=0.7 sin(xi1(t)),f(xi2(t)) = 0.5 cos(xi2(t))),f(xi3(t)) = 0.3 tanh(xi3(t)). In addition, the coefficient matrices are summarized as A = [-1.9057,3.05,-2.595;-3.97,0.04,2.23;4.405,-2.79,-1.54],B1=[-3,1,2;2,-5,3;1,4,-5],and
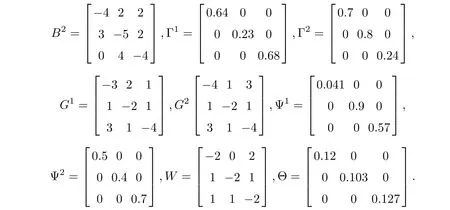
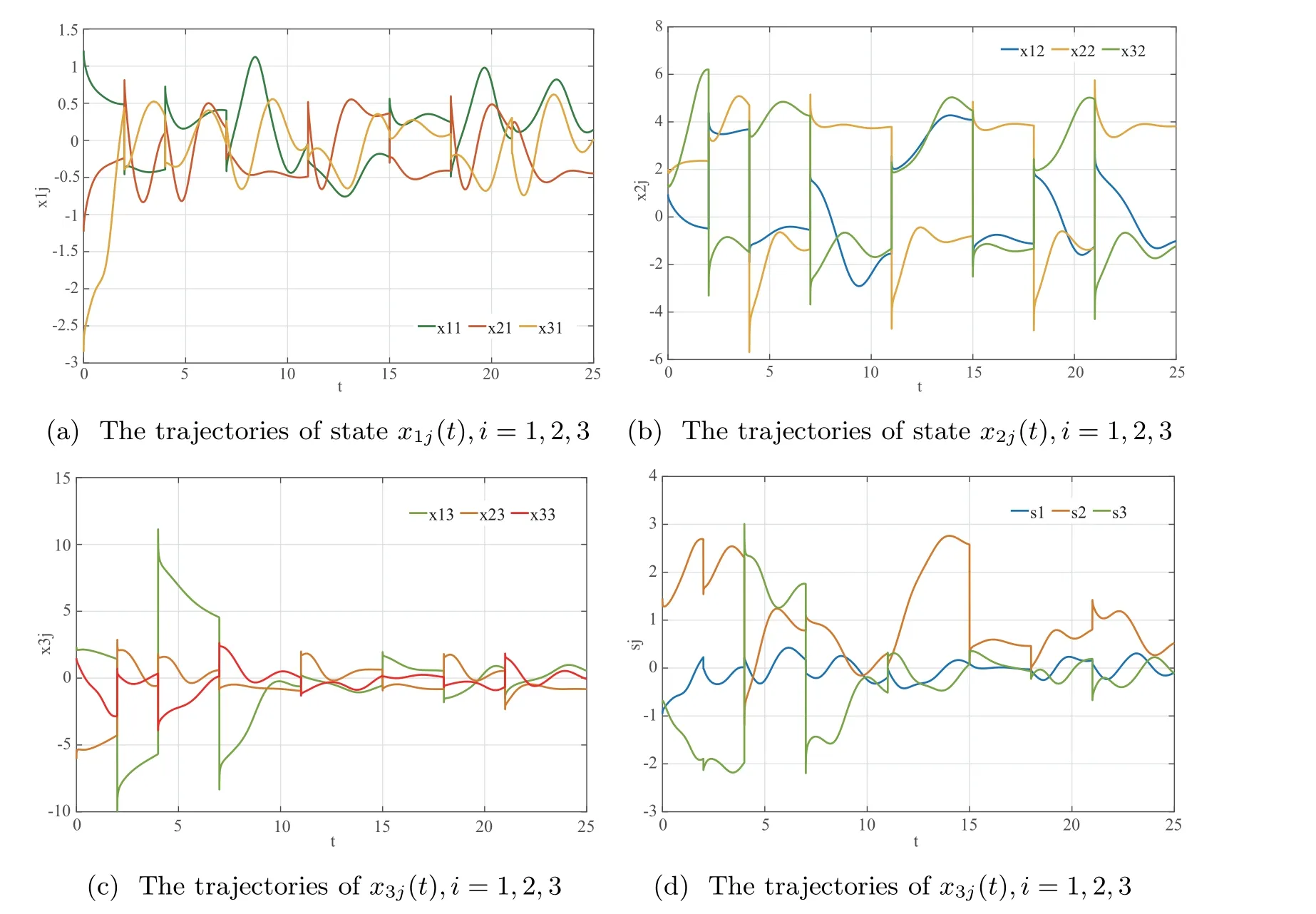
Figure 3 The trajectories of state xij(t) and sj(t),i,j =1,2,3 without controller


Figure 4 The trajectories of synchronization error eij,i,j =1,2,3
5 Conclusion
This article has discussed the global exponential synchronization issue for FCDNs with derivative couplings subject to impulse effects. Considering the designed feedback control scheme based on discrete time state observations, a significant lemma has been derived, establishing the connection between discrete and continuous time observations terms. By the Lyapunov stability theory and important fractional-order inequality, exponential synchronization criteria have been proposed in the form of LMIs. Finally, the efficacy of the presented results has been demonstrated by two simulation examples. A future research direction is to extend the results here to the synchronization for FCDNs with derivative couplings and timedelay via a fault-tolerant control strategy. In addition, it would be interesting to investigate the potential design of a fault-tolerant controller for when the topology structure of derivative couplings is nonlinear or discontinuous.
 Acta Mathematica Scientia(English Series)2022年2期
Acta Mathematica Scientia(English Series)2022年2期
- Acta Mathematica Scientia(English Series)的其它文章
- ARBITRARILY SMALL NODAL SOLUTIONS FOR PARAMETRIC ROBIN (p,q)-EQUATIONS PLUS AN INDEFINITE POTENTIAL∗
- SUP-ADDITIVE METRIC PRESSURE OF DIFFEOMORPHISMS*
- SHARP DISTORTION THEOREMS FOR A CLASSOF BIHOLOMORPHIC MAPPINGS IN SEVERAL COMPLEX VARIABLES*
- ON CONTINUATION CRITERIA FOR THE FULLCOMPRESSIBLE NAVIER-STOKES EQUATIONS IN LORENTZ SPACES*
- ON (a ,3)-METRICS OF CONSTANT FLAG CURVATURE*
- A NOTE ON MEASURE-THEORETICEQUICONTINUITY AND RIGIDITY*
