高中数学教学中化归思想的有效应用

福建省闽侯县第一中学 张 平

新课标强调,数学思想是高中数学教学的“四基”之一,是培育学生核心素养的重要依据,也是增强解决数学问题能力的有效途径,其中,化归思想形式简单、容易理解,具有重要的应用价值.

1 化归思想及其应用价值分析

“化归思想”是转化思想与归纳思想的统称,也是一种高效的数学解题思维方法.从数学教学实践维度看,化归思想的运用表现为“问题转化与归纳”上,即针对一个难度较大的问题A,通过转化为相对容易解决的问题B,在求出问题B的过程中掌握方法,形成经验,再还原到问题A的解决上.当然,从问题A到问题B的转化过程,以及从问题B到问题A的还原过程,是可以经历多重步骤的,如图1所示.

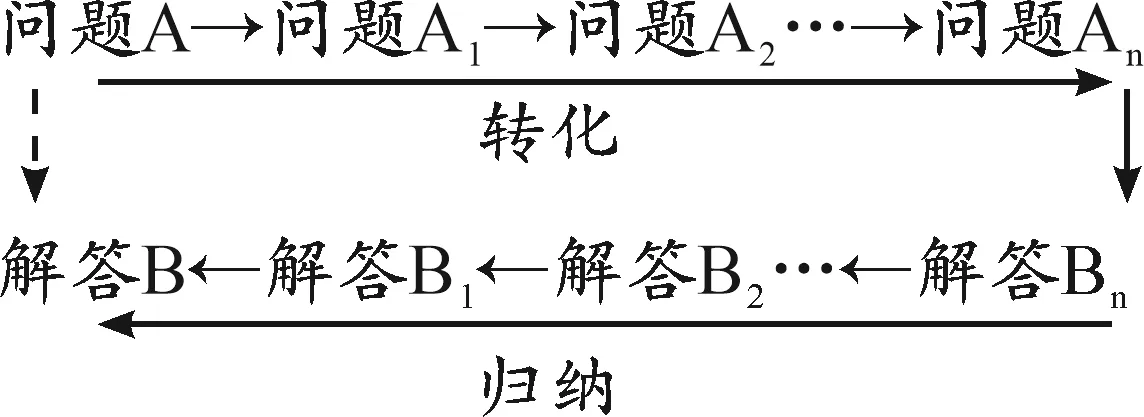
图1 化归思想应用示意图

数学化归思想的应用价值主要体现在三个方面.

1.1 从复杂到简单的化归

数学化归思想最显著的价值就是“化复杂为简单”,其具体方法很多,如“抽象变具象”“个性变标准”“数变形或形变数”“高层次变低层次”等.在高中数学教学的应用过程中,从复杂到简单的化归要保持灵活性原则,避免学生陷入思维定式,否则就违悖了化归思想应用的初衷.具体来说,可以将逆向思维、降阶思维等渗透到“从复杂到简单的化归”中去.

例如,在一平面直角坐标系内存在三条抛物线,y=x2+4ax-4a+3,y=x2+2ax-2a和y=x2+(a-1)+a2,其中至少有一条抛物线与x轴存在公共点,求实数a的取值范围.

结合题意分析,“与x轴存在公共点”意味着三个方程的判别式至少有一个应大于等于0.采用正向思维解答,需要分类判断判别式大于等于0的情况,不难看出计算量很大;结合化归思想与逆向思维分析,只需要考虑三条抛物线都和x轴不存在公共点的情况即可,即正确答案就是三个判别式“均小于0情况”的补集.

1.2 从隐含到已知的化归

进入高中之后,数学课程所表现出的抽象性特点更强烈,在许多问题的解决上,仅从表面难以得到充足的条件与信息.化归思想的应用价值之一,则是体现在“从隐含到已知”的转化上,本质上来说,也是对学生数学核心素养的训练,引导学生通过观察发现规律,进一步发掘隐含条件,反客为主.

1.3 从特殊到一般的化归

事实上,在数学教学活动中,经常会利用一些特殊情况来发现一般性结论,如在学习勾股定理时,“勾三股四弦五”就是直角三角形的“特殊三边关系”,但通过这一特殊的数学现象可以推导出a2+b2=c2的一般性结论.从学生学习角度出发,特殊性数学问题的解答往往相对比较容易,例如正弦、正切、余弦等的学习中,涉及特殊角(如30°,45°)时答案就很容易联想到,当然也存在相反的情况,即特殊性问题难度较高、一般性问题相对容易,这就涉及到从特殊到一般的化归操作.因此,采用化归思想中“从特殊到一般”的方式,同样可以起到降低难度、简化过程的效果.

例如,人教A版高中数学必修一“指数函数的概念”学习完毕后,教材中提供了一系列利用指数函数比较大小的问题供学生练习.类似“2 0212 022”和“2 0222 021”这样的情况,直接计算困难很大,可以先将这种“特殊性问题”做一般化处理.将原问题转化为nn+1和(n+1)n比较大小的问题,则:当n为1时,1<2;当n为2时,8<9;当n为3时,81>64,当n为4时,1 024>625;…….通过对一般化问题的穷举,最终可以认为当n≥3时,nn+1>(n+1)n.将这一结论应用于比较“2 0212 022”和“2 0222 021”大小的特殊情况下,从而判断出2 0212 022>2 0222 021.

2 高中数学教学中化归思想的有效应用

2.1 新课教学中化归思想的应用

基于前文对数学化归思想价值的分析,不难看出其在高中数学新课教学中的重要应用意义.一方面,高中数学教材在知识点的设置、分布上,采取的是分章节、单元的形式,这是国内各个版本数学教材的共同点,其优势是突出知识主题,但无形中造成了知识点的“隔阂”与独立.利用化归思想有利于增强新旧知识的关联,例如在“一元二次方程”的教学活动中,利用化归思想对一元二次问题进行降维,利用“十字相乘法”将其转化成一元一次方程的形式.另一方面,在化归思想的引导下,学生对新概念、新定理、新公式等的理解难度更小,例如在高中阶段的重点知识模块“函数”的教学过程中,可以采取“数变形”的化归方法,将函数解析式转化成对应的函数图象.

2.2 习题教学中化归思想的应用

“习题教学”是高中数学教学的常态化机制,既包括常规课程中穿插的习题讲解环节,又包括专门的“习题课”.在这样的教学情境中,化归思想的运用是非常普遍的,具体应用方式如“变式训练”“一题多解”“数形转化”等.值得注意的是,习题教学中应用化归思想的关键,在于引导学生自主探索,而不能教师简单、粗暴地把思路交给学生.

例如,利用化归思想展开变式训练,图2为四面体ABCD,其中B,C,D三点位置的三个角之和分别为180°,证明AB=CD,AC=BD,AD=BC.

图2

通过观察,直接基于四面体证明的难度很大,利用化归思想对立体图降维,转化为图3的形式(从点A将四面体“剪开”),再通过变式将原问题转化为平面几何问题.变式之后得到的条件中,可知A1B=A2B,A1C=A3C,A2D=A3D,加上“三个角之和为180°”的原题条件,即新生成的图形为平面三角形,证明过程就非常简单了.

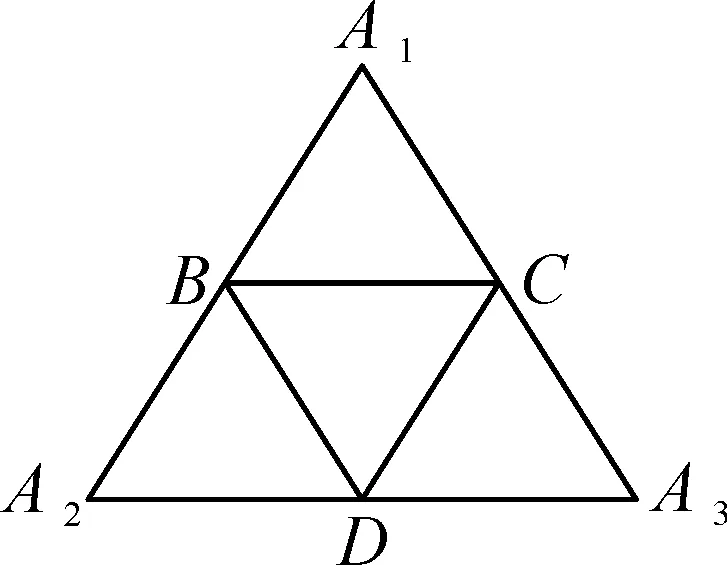
图3

2.3 复习教学中化归思想的应用

复习课是高中数学的重要课型之一,它的主要价值体现在“知识梳理”,即将高中阶段所学习的知识系统化、组织化,形成清晰的网络框架.将化归思想渗透其中,一方面有助于增强知识点之间的关联、对比,避免学生在知识运用过程中产生混淆,以此更牢固地掌握数学知识本质.另一方面,化归思想有助于增强学生数学知识的迁移能力,特别是在“从特殊到一般”的数学问题上,借助化归思想将碎片化、差异化的知识点转化成“学习支架”.

以人教A版高中数学选择性必修第二册第四章“数列”的复习课为例,整章复习内容主要包括数列的概念、等差数列、等比数列三部分.其中,后两部分可以视为“数列的概念”在不同维度的发展,教师可以选择两种数列的共性要素即“通项公式”,按照化归思想(由特殊到一般)梳理知识网络结构(如图4).

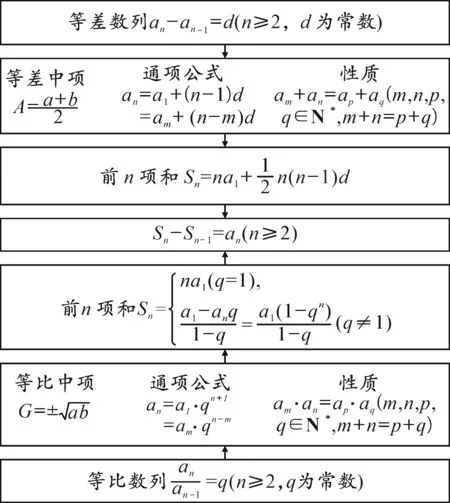
图4 数列知识结构图

综上所述,化归思想在高中数学教学中具有广泛的应用范围,除了新课传授、习题教学、课堂复习等场景中,还可以依据高中数学主要知识模块(如函数、数列、解析几何等)展开专门训练.在这一过程中,教师要注重化归思想运用的引导,采取“自主、合作、探究”等学习方法,在触类旁通、举一反三的思维框架下突显化归思想的应用价值,也能够很好地避免学生陷入定式思维的局囿.