阿基米德三角形的一个性质与圆锥曲线光学性质的邂逅*

广州大学附属中学(510006) 曹路路 朱惊涛

1. 引言

圆锥曲线的弦与过弦的端点的两条切线所围成的三角形叫做阿基米德三角形. 阿基米德三角形是高中解析几何中一个经典的双切线模型,在2021 年全国乙卷、2019 全国3卷、2018 年浙江卷、2012 年福建卷与江西卷、2008 年山东卷与江西卷、2007 年江苏卷和2006 年全国ⅠⅠ卷中均出现与之相关的高考试题. 试题呈现方式主要以抛物线和双曲线为载体,以阿基米德三角形为背景,考察学生在解决直线与圆锥曲线位置关系时的运算、逻辑推理、数学抽象思维等能力. 目前有诸多作者对其性质以及在高考试题背景方面进行了比较多的研究. 例如方亚斌老师文[1]中详细的列出了其各种性质并给出了详细的证明;况思怡、姚运国两位老师在文[2]中结合高考试题详细地分析了阿基米德三角形在高考试题中的命题方式与解题策略;另外还有王海燕老师的文[3]、谷留明老师的文[4]等众多文章. 除此以外还有唐明超、杨亚平两位高校老师在文[5]中基于文献分析的视角详细地对目前有关阿基米德三角形的研究文献进行了分类分析和总结. 但是笔者在众多文献中,发现鲜有作者深度探究阿基米德三角形与圆锥曲线光学性质的内在联系. 本文从抛物线中阿基米德三角形的一个与角度相关的性质出发,揭示了该性质与抛物线的光学性质的关系. 并将这一结论推广到椭圆和双曲线中去,重点从几何角度探讨阿基米德三角形这一性质与圆锥曲线光学性质的内在联系,使得阿基米德三角形这一经典问题在教学和试题命制中焕发新的生命力.该结论的推广与证明对我们的日常教学和命题研究有一定的价值.

2. 抛物线中的阿基米德三角形的一个性质及其证明

阿基米德三角形有许多性质,本文以抛物线为例,介绍其中一个与角度相关的性质.

题目1如图1,过抛物线y2= 2px(p＞0)上任意两点A、B分别作两条切线相交于点P,F是抛物线的焦点,连接FP,FA,FB,则恒有∠PFA=∠PFB.

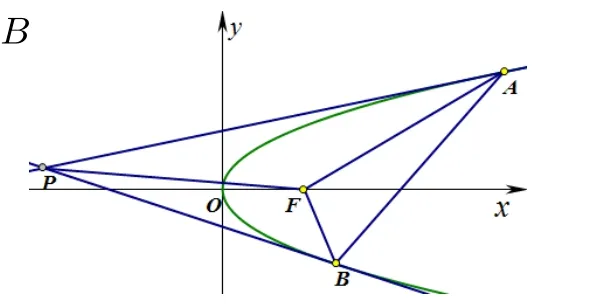
图1

证法二注意到点F是焦点,PA是过点A的切线,联想到抛物线的光学性质, 从点F发射的光线射到点A处, 其反射光线与x轴平行, 而这一性质等同于切线PA平分∠EAF(如图2),基于此,再结合抛物线定义,从而该题结论得证.

图2

3. 圆锥曲线的光学性质

圆锥曲线的光学性质在新人教A 版选择性必修第一册的第113 页的例5、第132 页例2 以及第140 页阅读与思考中都有出现,是圆锥曲线的重要特性. 简述如下:

抛物线的光学性质与对称轴平行的光线投射到抛物线上,经反射后反射光线必通过焦点;反之, 由焦点出发的光线投射到抛物线上, 其反射光线与对称轴平行.

图3

椭圆的光学性质从椭圆的一个焦点出发的光线投射到椭圆上,经过反射后反射光线必通过另一个焦点.

双曲线的光学性质从双曲线的一个焦点出发的光线投射到双曲线上,反射光线的延长线必通过另一个焦点.

图4

图5

关于圆锥曲线的光学性质的证明的文章比较多,这里不再给出,有兴趣的读者可自行查阅资料.

4. 推广

基于圆锥曲线的光学性质及定义,我们可以将题目1 中的阿基米德三角形的这一性质推广到椭圆和双曲线中.

推广1如图6, 已知点P在椭圆外, 过点P作椭圆两条切线, 切点分别是A、B,F1、F2是椭圆的左右焦点, 则∠PF1A= ∠PF1B,∠PF2A=∠PF2B.

图6

证明提示如图7, 延长F1A至M, 使得AM=AF2, 延长F1B至N, 使得BN=BF2. 根据椭圆的光学性质可知∠F2AP= ∠QAF1= ∠MAP, 易得ΔPAF2ΔPAM(SAS), 所以PF2=PM; 同理可得PF2=PN, 即PM=PN. 又F1M=F1A+AM=F1A+AF2= 2a, 同理,F1N= 2a, 即F1M=F1N, 从而可得ΔPMF1ΔPNF1(SSS),所以∠PF1A=∠PF1B.又∠PF2A= ∠PMA= ∠PNB= ∠PF2B,即∠PF2A=∠PF2B,命题得证.

图7

推广2如图8, 已知点P在双曲线外, 过点P作双曲线某一支的两条切线, 切点分别是A、B,F1、F2是双曲线的左右焦点,则∠PF1A=∠PF1B,∠PF2A=∠PF2B.

图8

证明提示如图9,在BF1上取点D,使BD=BF2;在AF1上取点E, 使AE=AF2. 根据双曲线的光学性质可知切线PB平分∠F1BF2,易得ΔPBD∽= ΔPBF2(SAS),所以PD=PF2; 同理可得PF2=PE. 又根据双曲线定义可知F1D=F1B-BF2= 2a=F1A-AF2=F1E,所以ΔF1DPΔF1EP(SSS),所以∠PF1B= ∠PF1A,又由∠F1DP=∠F1EP可知∠PDB=∠PEA,而∠PDB=∠PF2B,∠PEA= ∠PF2A,即∠PF2B= ∠PF2A,命题得证.

图9

通过以上的简要证明,可以看出阿基米德三角形的这一性质可以通过圆锥曲线的光学性质和定义获得,这反映了他们之间内在的联系. 而在揭示这种联系的过程中,我们又灵活运用了初中所学的“构造全等三角形证明等量关系”的方法,突出了几何证明的思想和初高中数学衔接的重要性. 事实上,因为圆锥曲线的定义就是一种几何的等量关系,故而从几何角度理解该性质的证明是很有必要且相当有趣的.