点接触轴承接触应力可靠性及灵敏度分析

赵振秀，刘军

（224057 江苏省 盐城市 盐城工学院 机械工程学院）

0 引言

滚动轴承作为机械系统支承与传递载荷关键的旋转元件，其可靠性决定了旋转机械系统的使用寿命，疲劳磨损和点蚀失效会造成滚动轴承失效，无法正常使用。因此轴承的可靠性直接决定了轴承和机械系统的运行可靠性。国内外很多学者对轴承接触应力进行了深入研究，主要基于Hertz 理论研究了轴承内部的应力分布情况[1-3]。张广萍等[4]采用Hertz 理论并考虑实际工况研究了轴承的应力分布；张胜伦等[5]研究并优化了结构参数对接触应力的影响。目前，鲜有学者针对轴承接触应力的可靠性及其灵敏度展开研究，其中在轴承接触应力的可靠性定量分析方面研究更少[6-10]。本文基于Hertz理论对接触应力计算方法进行精度研究，结合应力-强度干涉理论和二阶矩法研究点接触轴承的动态可靠性；对3 种接触应力计算方法进行精度验证和误差分析，建立点接触轴承动态可靠性模型，并进行动态可靠性及灵敏度计算与分析。

1 点接触轴承接触应力计算

1.1 接触应力计算模型

根据Hertz 理论，假定球轴承的滚动体与内外圈接触的表面区域为一旋转椭圆形，最大压应力出现在几何中心，其大小为

接触区域与接触应力分布如图1 所示。由图1可知，接触区域SC除中心点最大应力处以外其余点的法向应力为

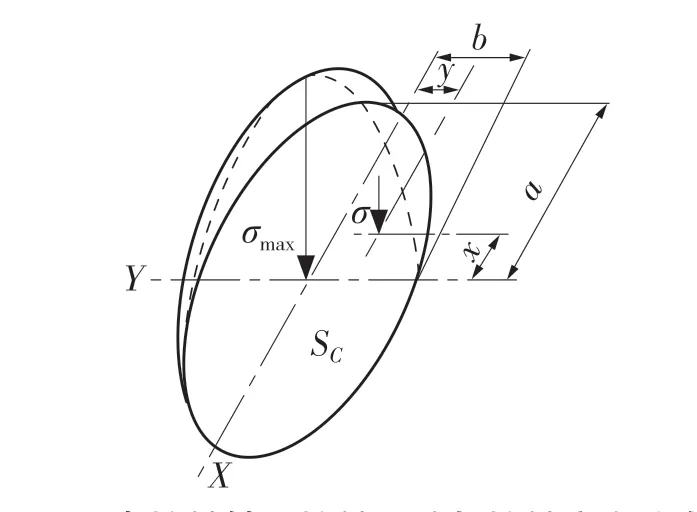
图1 点接触轴承接触区域与接触应力分布Fig.1 Contact area and contact stress distribution of point-contact bearing

式中：Q——承受载荷；a、b——接触椭圆的长、短半轴。

式中：a*、b*——接触椭圆半轴系数；Σρ——曲率和函数；E'——综合弹性模量。

在载荷Q的作用下，两物体由于弹性变形而形成接触区域SC。接触体表面的位移δ称为弹性趋近量，定义为

式中：δ*——弹性趋近系数。

式中：v1、v2——弹性接触体的泊松比；E1、E2——弹性接触体的弹性模量。

式中：Rix、Riy——滚动体和内（外）圈曲率半径；i=1、2，1 代表滚动体，2 代表滚道。Rix、Riy示意如图2 所示。

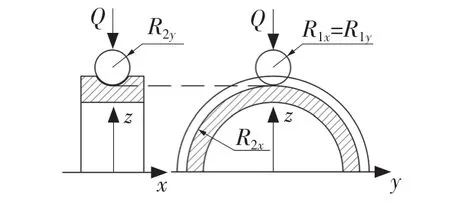
图2 Hertz 点接触曲率示意图Fig.2 Point-contact curvature diagram of Hertz

确定椭圆半轴系数a*、b*和弹性趋近系数δ*为

式中：e——椭圆参数；K(e)，E(e)——第1 类和第2 类完全椭圆积分函数。

1.2 接触应力的数值计算法

求解轴承接触应力问题的关键是根据曲率函数F(ρ)的值确定椭圆参数e，以及K(e)和E(e)。根据Hertz 理论模型，曲率函数F(ρ)是椭圆半轴a、b的函数

将式（14）变换成式（15）的形式以便求解椭圆参数e

式中：ε——一个微小误差控制量。

可通过牛顿迭代法求解式（15），获得e、K(e)和E(e)的值。

1.3 Hamrock-Dowson 经验法

从式（12）可以看出，当b/a无穷小时，K(e)的收敛很慢，但球轴承点接触问题恰巧属于此类情况，因此求解式（15）比较耗时。Hamrock 和Dowson 通过曲线拟合的方法给出了球轴承接触问题的近似经验公式为

由式（11）可知

1.4 拉格朗日插值法

基于数值计算法，罗继伟等[2]设计了一种单向均分法，便捷地获取轴承点接触参数；杨咸启[1]、Harris 等[3]给出了点接触半轴系数的参数表。根据上述学者的参数表绘制出触参数变化曲线，如图3所示，可见3 种参数表的变化趋势一致。采用拉格朗日二次插值公式，根据上述3 个参数表对半轴系数直接插值计算对应的y。由于点接触轴承的椭圆参数e接近于1，所以取部分参数如表1 所示，表中的第1 列数据标记为xi，需计算的某一列数据标记为yi，当已知x（xi-1＜x＜xi+1）时可以计算对应的y值

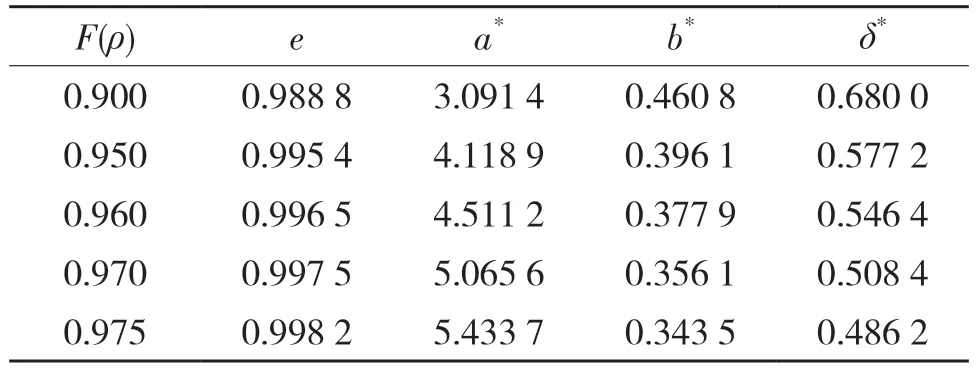
表1 无量纲接触参数Tab.1 Dimensionless contact parameters

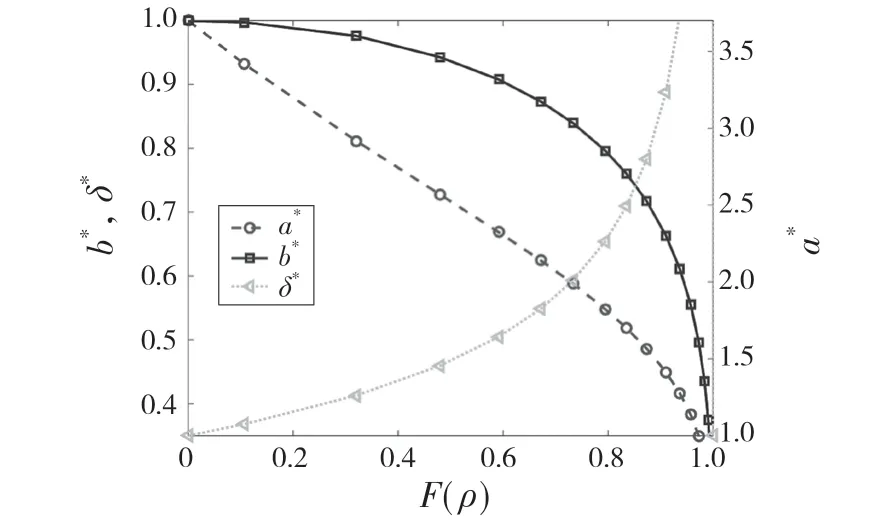
图3 无量纲接触参数变化Fig.3 Changes of dimensionless contact parameters

根据上述3 种不同的参数表结合Harris 等[3]的研究，对B218 角接触球轴承，计算点接触参数和内、外滚道最大法向接触应力，结果如表2 所示。对比结果可知：与数值解相比，3 种参数表的误差均不超过3%。其中文献[1]的参数表计算的结果更加准确。点接触轴承内滚道接触应力大于外滚道，这与文献[3]研究结果一致，因此，可靠性及灵敏度分析部分仅讨论内滚道接触应力。

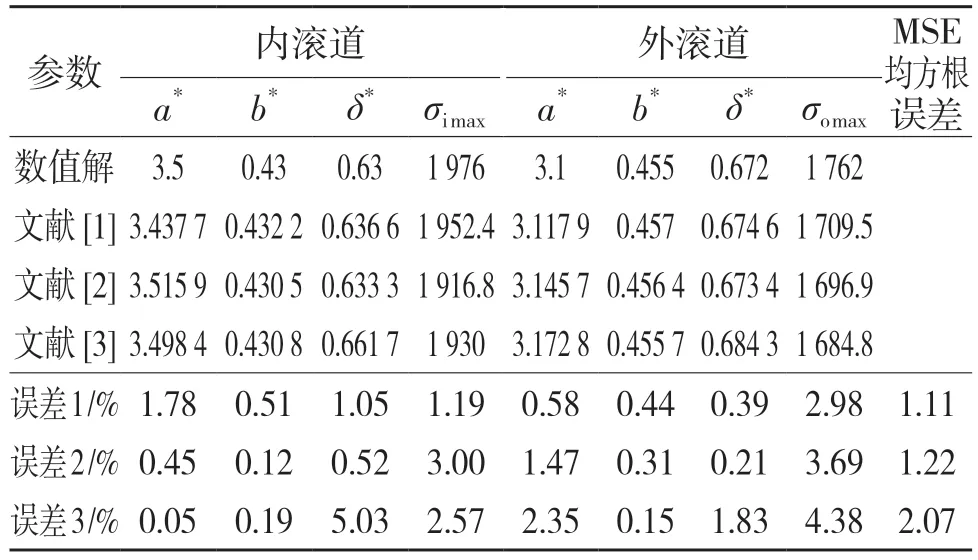
表2 拉格朗日插值法参数表误差分析Tab.2 Error analysis of Lagrange interpolation parameters

1.5 方法验证及误差分析

某机械旋转系统中，钢球与内滚道接触过程中，深沟球轴承钢球承受径向载荷为Q=1.5 kN 的静态载荷，系统运行过程中，同时承受最大径向载荷为2 kN 的动态载荷。已知钢球与内滚道的参数如表3 所示。采用上节所述3 种方法求解得出钢球与内滚道的最大接触应力随径向载荷的变化趋势如图4 所示。

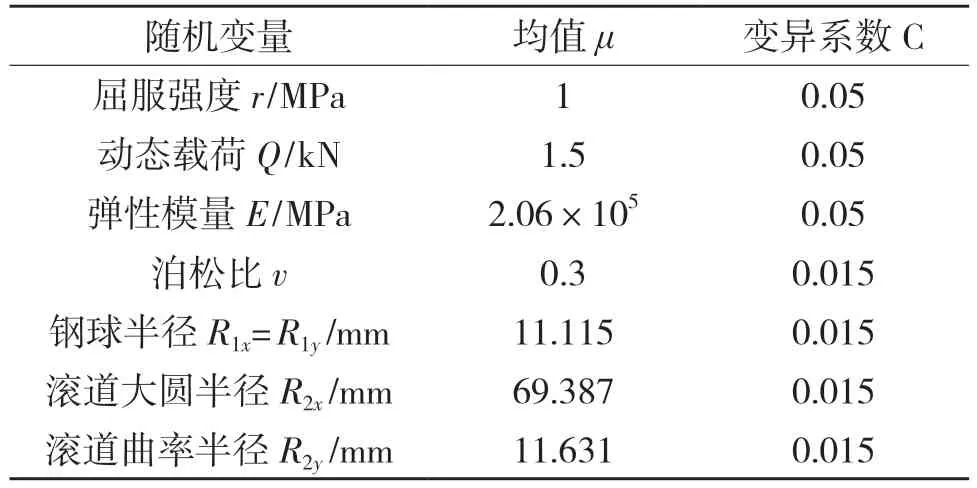
表3 随机变量参数表Tab.3 Random variable parameters

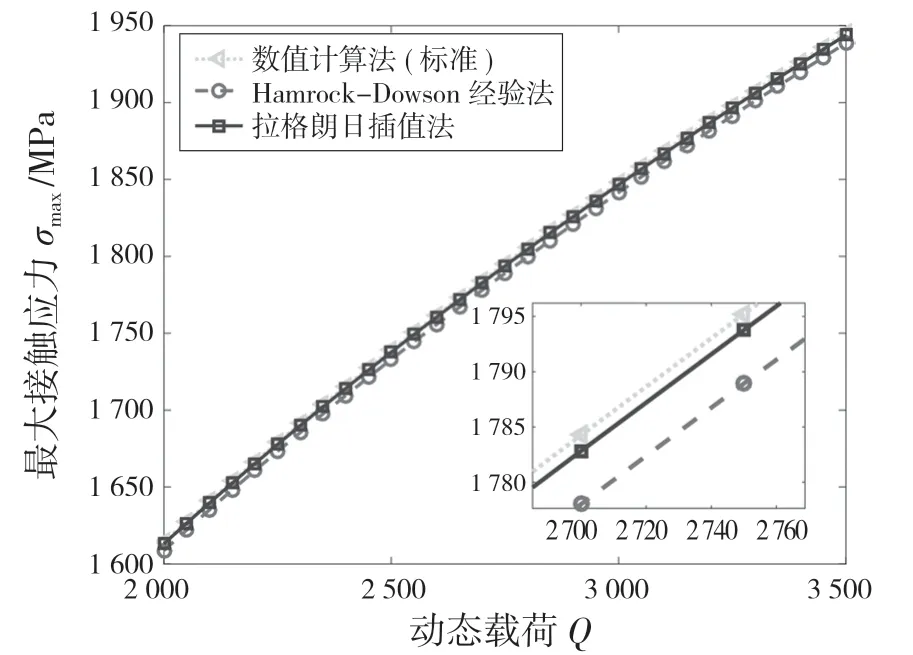
图4 3 种方法计算的最大接触应力对比 Fig.4 Comparison of the maximum contact stress calculated by three methods

由图4 可知，拉格朗日插值法相较Hamrock-Dowson 经验法更加逼近数值计算法计算的点接触轴承接触应力。两者相对误差如图5 所示，2 种方法的相对误差均小于0.4%，其中拉格朗日插值法的相对误差小于0.1%。因此，2 种方法均可代替数值计算法用于计算点接触轴承接触应力，其中拉格朗日插值法计算结果更加准确。

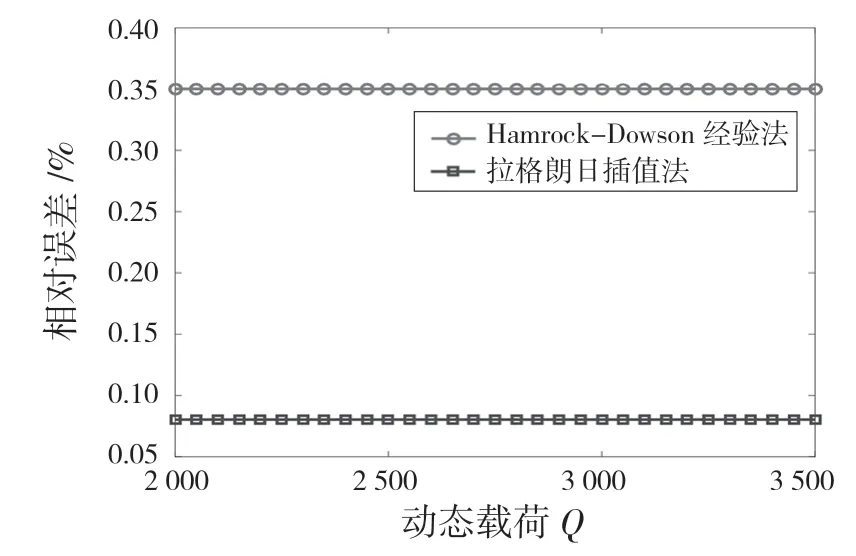
图5 接触应力相对误差Fig.5 Relative error of contact stress

2 动态可靠性分析

由上述分析可知点接触轴承最大接触应力呈逼近线性趋势，因此采用二阶矩方法可以满足其最大接触应力可靠性及灵敏度分析。

2.1 动态可靠性模型

根据赫兹接触应力计算理论[3]，点接触轴承滚动体与滚道的最大接触应力为

根据应力-强度干涉理论建立机械系统的状态方程

式中：r——屈服强度；g(X)≤0 时表示结构功能失效。

引入动态可靠性指标β(t)简化可靠性的分析计算，可靠性指标β(t)的定义为

式中：E[g(X,t)]——状态函数g(X,t)的平均值；Var[g(X,t)]——状态函数g(X,t)的方差。

如果基本随机变量X服从正态分布，则可以计算出结构的可靠度R(t)为

式中：φ(·)——标准正态分布函数。

当强度和所受应力服从正态分布时，采用二阶矩法，只需要知道随机变量的均值和方差，即可计算出系统的可靠度[6]。

不考虑g(X) 2 阶以上的部分，取近似的g(X) 2 阶均值和1 阶方差

式中：Var(X)——随机变量的方差矩阵。

状态函数g(X)对随机变量X的偏导数为

这种求解方式得出的是近似结果，其最大特点是求解过程简便，具备较强的适应能力，当非线性不是太高时，其求解的精度可以满足工程实际的要求。

2.2 点接触轴承动态可靠性分析

根据应力-强度干涉可靠性模型，结合最大接触应力模型，设动态载荷Q在[0，1]s 内随时间线性递增并达到最大值，选取随机变量X=[r Q E v R1x R1y R2x R2y]。在缺乏充足的实验数据的前提下，可以通过变异系数C估计随机设计参数的标准方差[10]，具体见表3。采用该模型作为基于应力-强度干涉理论的状态方程，可以获得点接触轴承的应力-强度可靠性模型。

利用式（22）获取最大接触应力随时间变化的曲线如图6 所示。由图6 可知，轴承最大接触应力在2.69 kN 时超出其屈服强度，根据应力-强度干涉理论建立的动态可靠性模型定义，判定此时的轴承处于失效状态。

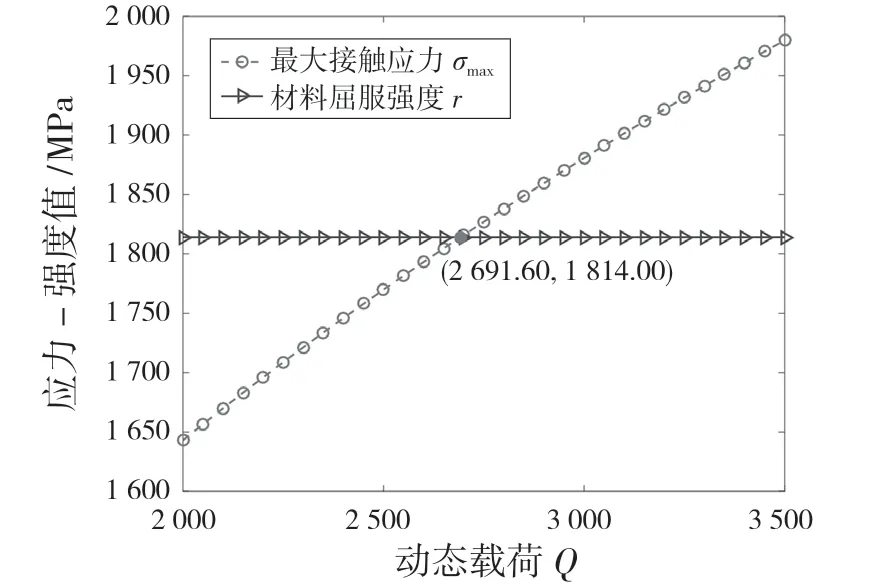
图6 轴承点接触应力-强度状态图Fig.6 Stress-strength state diagram of point-contact bearing

根据式（24）、式（25）计算动态可靠度，可靠度随时间变化曲线如图7 所示。由图7 可知，轴承的可靠度在22 ms 时出现下降趋势，说明其在22 ms 时已经出现了早期失效的可能。采用蒙特卡洛法对随机变量X抽样后，根据状态方程计算的基于蒙特卡洛法的可靠度验证了二阶矩法计算的动态可靠度结果的精度。

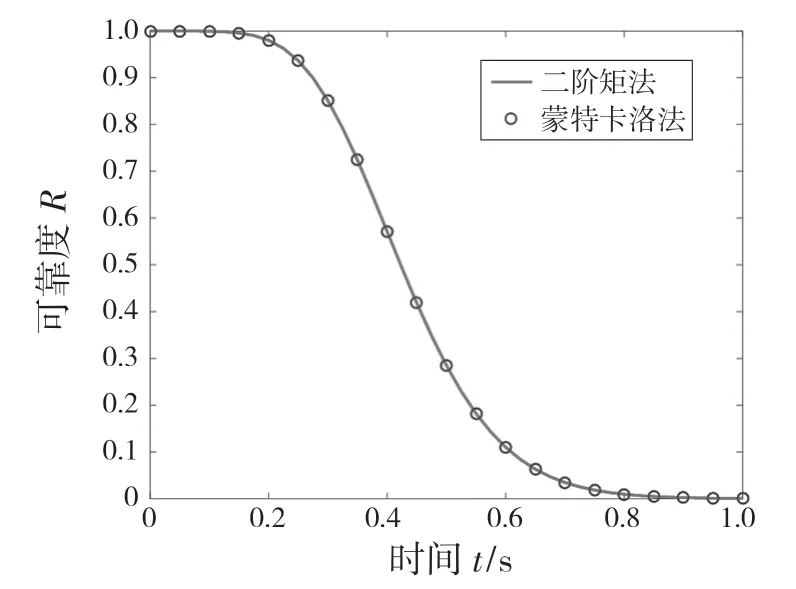
图7 动态可靠度曲线Fig.7 Dynamic reliability curve

3 动态可靠性灵敏度分析

3.1 动态可靠性灵敏度理论

机械结构可靠性灵敏度分析基于可靠性的敏感度分析，通过计算得出随机变量对机械结构可靠性的影响，能较好地反映各随机变量对机械结构的影响[7]。

机械结构的可靠性灵敏度分为对随机变量X的均值可靠度灵敏度dR(t)/d和方差可靠性灵敏度dR(t)/dVar(X),计算公式分别为

3.2 动态可靠性灵敏度分析

通过式（30）计算均值灵敏度随时间变化的曲线，如图8 所示。由图8 可知，随机变量钢球半径R1x、R1y和滚道曲率半径R2y对动态可靠性模型的灵敏程度呈正相关趋势，即增大随机变量的均值，可提高系统运行的可靠性，反之亦然。在安全域内，各随机变量灵敏度相差不大；当轴承失效后，轴承材料泊松比ν对系统运行的影响最大，随机变量钢球半径R1x、R1y次之，再次是滚道曲率半径R2y，而其他随机变量对系统的影响均可忽略不计。因此在生产制造过程中，通过增大轴承的钢球半径R1x、R1y和滚道曲率半径R2y、减小轴承材料的泊松比ν可以提高机械系统运行的可靠性。

通过式（31）计算轴承方差灵敏度随时间变化的曲线，如图9 所示。由图9 可知，在系统运行完全失效前，增大各随机变量的标准差会降低系统可靠性；失效后，增大各随机变量的标准差会提高系统可靠性。因此在设计制造过程中，可通过减小轴承材料泊松比ν的标准差提高系统运行的可靠度。

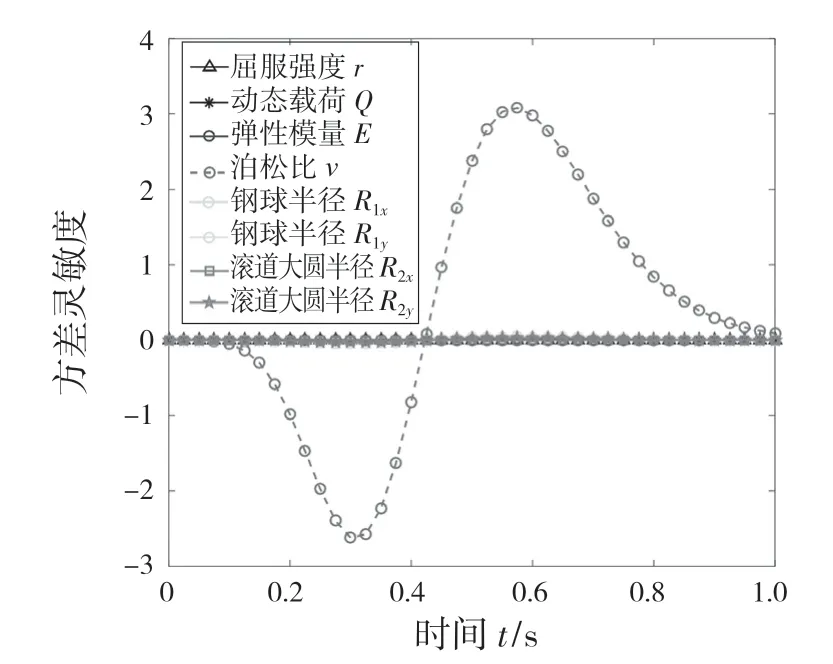
图9 随机变量方差灵敏度Fig.9 Sensitivity of variance of random variables

4 结论

（1）基于Hertz 理论研究了点接触轴承最大接触应力3 种不同的计算方法：数值计算法、Hamrock-Dowson 经验法和拉格朗日插值法研究了拉格朗日插值法中3 种计算点接触的无量纲参数表。结果表明：拉格朗日插值法计算结果更加准确。

（2）根据应力-强度干涉理论建立了点接触轴承的最大接触应力动态可靠性模型，采用二阶矩法对轴承动态可靠性进行求解，并采用蒙特卡洛法验证。结果表明：点接触轴承的可靠度随动态载荷增加而减小。结合文中算例，轴承承受最大径向载荷不能高于2.69 kN。

（3）根据可靠性灵敏度分析相关理论，求得点接触轴承动态可靠性模型中随机变量对模型的灵敏度。结果表明：增大轴承的钢球半径和滚道曲率半径、减小轴承材料的泊松比及其标准差可以提高机械系统运行的可靠性。