图的双罗马控制数的上界
郝国亮,庄蔚,谢智红,曾淑婷
(1.菏泽学院 数学与统计学院,山东 菏泽 274015;2.东华理工大学 理学院,江西 南昌 330013;3.厦门理工学院 数学与统计学院,福建 厦门 361024;4.菏泽学院 商学院,山东 菏泽 274015)
图的控制理论是图论中的一个重要研究分支,具有较强的应用背景[1].基于不同的实际背景,提出了各种不同的控制参数,如符号罗马边控制[2]、电力控制[3]、外独立意大利控制[4]、跳跃控制[5]、经典控制[6]、罗马控制[7]以及符号混合控制[8]等.各种控制参数的研究不仅丰富和发展了图的理论,而且也在应用领域如计算机科学、计算科学及网络工程等得到了很好的应用[1].对于最小度至少是2的n阶连通图(五圈图除外),Chen[9]证明了其双罗马控制数不会超过[13n/11].Henning等[10]刻画了双罗马控制数.Jafari 等[11]证明了即使是确定二部图和弦图的双罗马控制数问题也是NP-完全问题.因此研究双罗马控制数的上下界问题显得尤为重要.目前文献 [9-10]主要利用图的顶点数来确定双罗马控制数的界,因此很有必要考虑利用其他图参数研究双罗马控制数的界.本文将研究图的双罗马控制数的上界问题,利用图参数(如顶点数、直径、最小度以及填装数等)得到了双罗马控制数的一些新的上界,部分改进了Chen[9]给出的结果.
1 预备知识
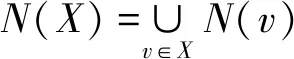
2016年,Beeler等[13]引入了图的双罗马控制的概念.称函数f:V(G)→{0,1,2,3}为图G的双罗马控制函数,如果任意赋值为0的顶点都至少邻接1个赋值为3或2个赋值为2的顶点,并且任意赋值为1的顶点都至少邻接1个赋值为2或3的顶点.图G的双罗马控制函数f的权为ω(G)=∑v∈V(G)f(v).图G的双罗马控制函数的最小权称为G的双罗马控制数,记为γdR(G).权为γdR(G)的双罗马控制函数称为γdR(G)-函数.
2 结论及证明
Beeler等[13]给出了如下结论:
引理1[13]设Pn是含有n个顶点的路,则
利用引理1,可以得到双罗马控制数的如下上界.
定理1设G是n阶连通图且设diam(G)=D,则
证明:设P是图G的一条直径路且设f是一个γdR(P) -函数.显然|V(P)|=D+1.定义函数g:V(G)→{0,1,2,3}使得
不难看出,g是G的一个双罗马控制函数.因此如果D≡2(mod 3).则由引理1知,
γdR(G)≤ω(g)=ω(f)+2(n-|V(P)|)=(D+1)+2(n-D-1)=2n-D-1.
类似地,可以证明如果D≡0(mod 3)或D≡1(mod 3),则γdR(G)≤2n-D.
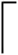
定理2设G是最小度至少为3的n阶连通图且设diam(G)=D,则
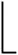
如果D≡0(mod 3),则定义函数f:V(P)→{0,1,2,3}使得
不难验证,在每种情况下,函数f是直径路P的一个双罗马控制函数并且
由于P是图G的一条直径路,故对于任意不相等的非负整数i和j,均有N(v3i+2)∩N(v3j+2)=φ成立.定义G的一个双罗马控制函数g:V(G)→{0,1,2,3}使得
注意到X中的每个顶点至少有δ-2个邻点在V(G)-V(P)中,即对任意v∈X,|N(v)-V(P)|≥δ-2.因为直径D除以3的余数为0,1,2,所以接下来只需要考虑如下3种情形即可.
情形1:D≡1(mod 3).
因为顶点vD+1至少有δ-1个邻点在V(G)-V(P)中,即(N(vD+1)-V(P)|≥δ-1,所以
(D+2)+2(n-D-1-(δ-2)(|X|-1)-(δ-1))=(D+2)+2(n-D-1-
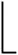
情形2:D≡2(mod 3).
在这种情形下不难验证
情形3:D≡0(mod 3).
首先假设N(vD+1)⊆N(vD-1),注意到
|N(vD-1)-V(P)|≥|N(vD+1)-V(P)|≥δ-1.
于是顶点vD-1至少有δ-1个邻点在V(G)-V(P)中,即|N(vD-1)-V(P)|≥δ-1.因此
(D+2)+2(n-D-1-(δ-2)(|X|-1)-(δ-1))=(D+2)+2(n-D-1-
下面假设N(vD+1)不是N(vD-1)的顶点子集,则存在某个顶点u∈N(vD+1)-V(P)使得u∉N(vD-1).定义G的双罗马控制函数g′:V(G)→{0,1,2,3}使得
于是
(D+2)+2(n-D-1-(δ-2)|X|-1)+1=(D+2)+2(n-D-2-
考虑到定理2的条件中需要连通图的最小度至少是3,下面利用图的填装数给出不受最小度限制的图的双罗马控制数的上界,进一步改进定理1的结果.
定理3设G是任意n阶连通图,则γdR(G)≤2n-(2δ-1)ρ(G).
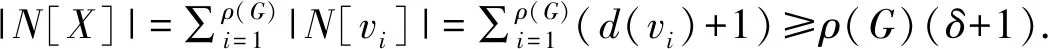
定义函数f:V(G)→{0,1,2,3}使得
不难验证f是G的一个双罗马控制函数,因此
3ρ(G)+2n-2ρ(G)(δ+1)=2n-(2δ-1)ρ(G).
3 结论
本文研究了图的控制理论中一个新的控制变量,即图的双罗马控制数的上界问题.通过对一般图的结构分析,得到了连通图的双罗马控制数的若干新的上界,这些上界与图的顶点数、直径、最小度以及填装数密切相关.
