突出问题解决 发展高阶思维*

广东省广州市艺术中学 吴荣燕

培养高中生数学高阶思维能力,主要是要发展学生的探究创新、批判质疑、直观想象、问题解决等能力.从数学教学的角度来看,教师要深刻理解教学内容,挖掘其蕴含的高阶思维培育素材,在课堂上创设情境,引导学生开展深度学习,促成高阶思维的发展.

1 教学过程

下面以人教A版(2019)“余弦定理、正弦定理”的新授课教学设计为例,展示应如何在课堂中培养学生问题解决的能力,发展高阶思维.

1.1 生成目标问题

问题1三角形是我们非常熟悉的几何图形,构成一个三角形的基本要素有哪些?

生1:三条边和三个角,一共六个基本要素.

问题2我们学过的全等三角形的判定定理有哪些?

生2:有“SAS”“SSS”“ASA”.

师:这是“定性”的结论.在△ABC中,试找出边和角之间的“定量”关系.

设计意图：把握事物的本质,是建构知识结构的前提.从学生熟悉的全等三角形判定定理出发,引导学生从定性的研究转向定量的探究.

1.2 启发引导思考

问题3如图1,在△ABC中,如何用边、角的关系来表示三角形的面积S?

图1

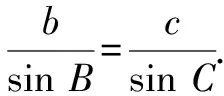
师:这便是“正弦定理”,其实质是三角形面积公式的推论.

生5质疑:上述“正弦定理”对任意三角形都成立吗?

学生讨论直角、钝角三角形的情形.

师:结构对称的正弦定理实际上是三角形面积公式的推论.

设计意图：正弦定理充分体现了“对称支配力量”的数学美感,可作为学生认识数学审美价值、人文价值的一个切入口.

1.3 明晰探究路径

问题4要探究三角形的边与角的定量关系,还可以运用哪些工具?

生6:平面向量,它兼具数与形,既有大小又有方向.

问题5在△ABC中,存在着哪些恒成立的向量关系式?

问题6如何将上述向量等式数量化呢?

生8:两边同时平方,用数量积的方法展开.

生9:两边同时与同一个向量作数量积运算.

设计意图：抓住向量法的根本,帮助和引导学生养成用向量法解决几何问题的习惯,掌握解决此类问题的一般研究方法.

1.4 引导合理论证

活动一：两边平方作数量积运算

生10:两边同时平方,整理,得a2=b2+c2-2bccosA.同理,b2=a2+c2-2accosB,c2=a2+b2-2abcosC.

师点评:上述三式即为余弦定理.勾股定理是余弦定理的特殊化.

活动二：两边同时用a,b,c中的某个向量与其作数量积运算

生11:由a=b-c,得a·a=(b-c)·a,化简得a=bcosC+ccosB(①);由“对称性”,得b=acosC+ccosA(②),c=bcosA+acosB(③);联立方程①②③可得余弦定理.

师补充:式①②③为“射影定理”.

设计意图：使学生聚焦数量积运算,通过探究获得对向量法的深刻理解,突破最近发展区,进入批判性思考阶段.

问题7设i,j分别是平行和垂直于向量a的单位向量,请继续探究向量等式的数量积运算.

活动三：两边同时与i作数量积运算

生12:可得a=bcosC+ccosB,后续与“活动二”相同.这个数量积运算省去约分的步骤,简化了计算过程.

活动四：两边同时与j作数量积运算

生13:若b,j的夹角为锐角,化简后为bsinc=csinB,可得正弦定理.夹角为钝角时结论相同.

问题8向量的数量积运算是如何实现余弦定理和正弦定理转化的?

生14:通过构造与已知向量垂直的单位向量,实现构造角之间的互余关系.

设计意图：采用“说数学”的教学策略,让学生讨论构造单位正交基带来的简化与变化,激发学生的分析、评价、创造等高阶思维.

1.5 课堂回顾反思

问题9这节课我们通过哪些方式推导出了正弦、余弦定理?体现了哪些数学思想方法?

设计意图：体会知识的生长过程和向量的工具价值.归纳本节课渗透的数学思想方法,进一步发展分析、评价、创造等高阶思维.

问题10本节课中从哪些角度,提出了哪些关键问题?

设计意图：激发学生思考“问题的问题”,让他们学会发现问题、提出问题,进而培养高阶思维,促进深度学习的发展.

2 指向高阶思维的数学课堂教学反思

核心素养、高阶思维的培养和发展必须以数学课堂为阵地,以学生为主体、教师为主导来开展,本节课的“高阶思维”课堂教学动线如图2所示.

图2 “高阶思维”课堂教学动线

2.1 关注单元教学,提高问题解决能力

高阶思维的培养,需要教师关注单元教学,基于学科本质凝练系统化的知识,获取知识的内在联系和蕴含的高阶思维,使得学生头脑中的知识群之间具有关联性、逻辑性.

2.2 注重知识的生成,培养探究创新能力

教师要引导学生通过探究交流等方式理解知识的发现过程,从而培养学生的探究创新等高阶思维能力.

本节课从三角形的基本要素出发,引导学生对三角形的研究从定性转向定量,寻找三角形的向量等量关系式,将向量关系转化为数量关系式等发散式问题,这些均是在创设知识的“生长点”.在四个探究活动中,学生经历了数量积的几何意义,如a2=|a|2,a·e=|a|cosθ(e为单位向量)和a⊥b⟺a·b=0,运用向量法最终实现对余弦定理、正弦定理的互证.由此学生理解到,三角形的各种几何量之间可以互相表达,从而可能进一步发现其他证明方法,增强创新意识与能力.在解决新问题时,才更易理解问题实质,并提取、运用已学知识经验,通过分析与综合进行高阶思维活动.

2.3 创设交流平台,激活批判质疑能力

在认知发展的过程中,思维的外化需要学习者作出相关的陈述,理解他人的陈述,相互论证或挑战各自的观点或假设.所有这些过程都将直接导致高阶思维活动和高阶学习.“说数学”是指个体用口头表达自己对数学问题的理解、解决数学问题的思路以及数学学习情感等的数学学习活动.

2.4 重视育人价值,促进个体主动发展

深度学习并不只是对浅层学习的反对,也并不只停留于学生高阶思维的培养,而是要促进学生作为具体的社会历史实践主体的成长和发展.

数学学科在培养学生理性思维、科学精神和促进智力发展的过程中发挥着重要作用.本节课注重联系初中所学过的三角形边角的定性关系,结合学生的最近发展区,鼓励学生运用类比、转化、分类与整合等多种方法探究三角形边角的定量关系,自然而然地引入向量作为工具,揭示向量的本质属性.学生在教师的引导下,经历正、余弦定理的推导过程,领悟向量法所蕴含的数学思想;在“说数学”活动中发展提出问题、批判质疑、合作交流的能力;在对三角定律的深入学习中,培养高阶思维,感受数学家严谨、求实的责任担当,让学生对社会的发展产生责任感和使命感.这也是对深度学习理念的任务与目标的体现和落实.

深化课程改革精神,需要教师从自身的教学出发,关注学生的深度学习和主体发展,通过知识的教学达成全面育人的目的.如何通过培养数学高阶思维促进核心素养的落地,还需要教师不断反思和探索.