基于多边形维诺图的梯度弹性多孔结构设计

陈小满，谢卓尊，曹 伟*

（1.厦门华厦学院，厦门 361024；2.华侨大学 机电及自动化学院，厦门 361021）

0 引言

梯度多孔结构因其具有比强度高、比表面积大、轻量节材、弹性/硬度可定制等优点，被广泛应用于汽车、航空航天、军事、医疗等众多领域。但由于梯度多孔结构具有极为复杂的内部结构，难以通过传统加工装备和工艺进行制造，限制了其功能的发挥[1]。近年来，由于增材制造技术的快速发展，使梯度多孔结构的制造成为可能。相比于粉末冶金、渗透铸造、金属沉积等制造方式，增材制造能通过多孔结构的数字化模型，实现更加精准的制造[2]。增材制造技术使梯度多孔结构具有更高的设计自由度，即可以自由定制孔的分布而不用考虑复杂结构带来的传统制造约束，因此对梯度多孔结构的设计提出了更高的要求。

梯度多孔的设计要求包括：

1）多孔结构的孔隙分布满足几何、力学性能的需求[3-4]；

2）多孔结构的设计满足不同增材制造工艺的制造约束[5-6]。目前，大多数梯度多孔结构均是针对SLA、SLS等工艺，这些工艺要求多孔结构必须是全连通的[2-7]，以保证在打印完成后孔腔内部的材料（粉末、液体）能够取出，因此基于这些工艺的梯度多孔结构多采用类似支杆连接的几何结构[8-9]。如Liu等提出的一种各向同性三维维诺多孔结构，通过隐式曲面构建维诺胞元的内部孔腔和胞元间的甬道，实现全连通[10-11]。Wu等提出一种应力驱动的支杆晶格结构，该结构不仅能够根据应力大小调整晶格密度，还能根据应力方向调整晶格朝向[12]。

而对于使用最广泛、设备和材料价格最便宜的FDM工艺，具有完全不同的制造约束。首先，由于FDM是通过逐层堆积熔融材料实现对目标物体打印的，因此要求所打印物体必须满足支撑要求[13-14]。而上述支杆多孔结构存在大量过度悬垂的支杆，必须额外添加内部支撑结构才能进行打印，造成打印材料和时间消耗增加。此外，由于这些内部支撑结构在打印后无法去除，会造成打印出的多孔结构和所设计的梯度多孔结构不相符，其力学性能也会发生改变[15]。再次，上述支杆多孔结构的每个切片层都包含大量相对孤立的椭圆（实体部分），导致FDM无法实现连续的喷丝打印，会产生大量拉丝，严重影响打印质量。因此，这些设计的梯度多孔结构并不适合采用FDM工艺打印。

基于此，本文聚焦于针对FDM工艺的梯度多孔结构设计。在几何结构方面，提出一种基于多边形维诺图的自支撑梯度弹性多孔结构建模方法，建立闭孔的三维多边形维诺多孔结构，在确保实现多孔结构自支撑的同时，还能实现切片层的连续打印。此外，在梯度设计方面，首先研究了设计参数对所设计的维诺多孔结构的几何度变化的影响规律；其次，通过数值均质化方法，研究了设计参数对其弹性性能的影响规律，从而实现对其梯度弹性分布的控制。

1 自支撑多边形维诺多孔结构建模

1.1 自支撑约束

如图1所示，定义悬垂角ω为法向量与打印方向的夹角，其中。在3D打印的过程中，由于熔融的材料无法做到瞬时固结，当前打印层超出下一层部分过多时，即当当前打印区域的悬垂角大于材料的最大悬垂角ωmax时，会产生悬垂处材料的塌陷现象，影响成型精度，因此需要在悬垂材料的下方添加额外的支撑结构。

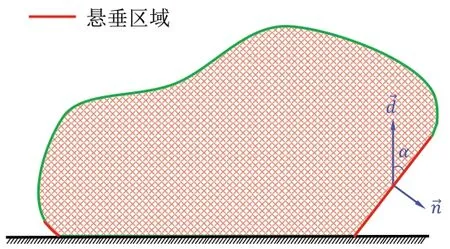
图1 3D打印的悬垂角

对于FDM工艺来说，最大悬垂角ωmax仅与所使用材料的性能有关，如熔融状态下流体的黏度等，每种材料的悬垂角会存在一定的差别，大多在45°左右。因此，本文将最大悬垂角设定为ωmax=45°，当模型某区域的悬垂角度ω＞ωmax时，需要在下方添加支撑；相反地，当ω≤ωmax时，不需要添加额外支撑。当模型所有区域的悬垂角ω均小于最大悬垂角ωmax时，称该模型为自支撑模型。

1.2 多边形维诺图

1.2.1 维诺图

其中，q为空间中的任意点，d(si,q)和d(sj,q)分别为点q到站点si和sj的距离，即站点si所对应的维诺区域Ri(si)由所有距离站点si最近的所有空间点组成。因此，由站点集S定义的维诺图为S中所有站点对应的维诺区域的并集，即

1.2.2 多边形维诺图

在式(1)中，根据“距离”d的定义不同，所得到的维诺图也不相同。图2所示为二维平面中站点集S相同时不同“距离”所对应的维诺图，从左至右的“距离”分别为欧几里得距离（圆形），切比雪夫距离（正方形），曼哈顿距离（菱形）以及三角形距离。

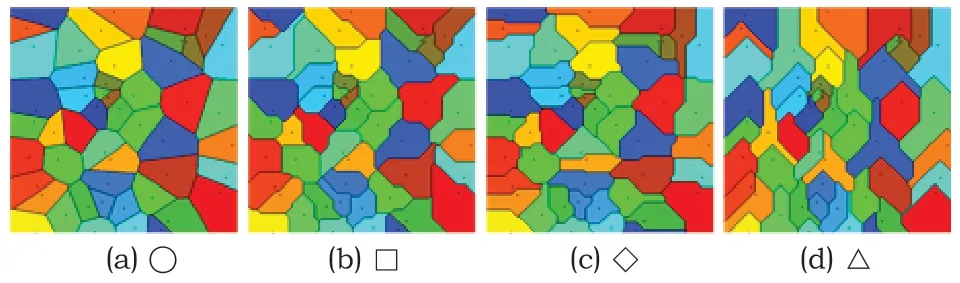
图2 二维空间中不同距离定义的维诺图

图2最右侧的三角形距离定义下的维诺图的所有边均能满足自支撑约束，而其他三种维诺图中存在部分不满足自支撑约束的边，例如存在水平的边，从而无法直接通过FDM打印机进行成型。事实上，图2中的四种图形均属于多边形的实例，且均呈现出相同的特性——其维诺边（面）的朝向的数量n是常数[16]，如正方形和菱形距离下n=4，三角形距离下n=3，且在三角形距离下所有的维诺边和竖直方向（打印方向）的夹角均小于或等于45°，即满足ω≤ωmax，说明在二维空间中三角形距离对应的多边形维诺结构是自支撑的。

给定一个内部包含原点的凸多边形P，从点p到点q的多边形距离定义为：

其中，多边形距离dP(p,q)为将多边形P从圆点O移动到p点，并缩放t倍后使其能包含q点的最小t的值，如图3所示。

图3 多边形距离

多边形距离dP(p,q)的计算方式为：设q′为多边形p+P与p到q的射线相交的唯一点，则：

其中，||q-p||和||q′-p||分别为空间中点q、q′、到p点的欧氏距离。

1.2.3 三维空间多边形距离

将二维空间中的等腰三角形拓展至三维空间，可以建立三维自支撑多孔结构。本文选取了一种特殊的多面体——k-棱锥，如图4所示。该棱锥的底面是正k边形，棱锥具有k个侧面。为方便描述，本文将二维空间中的三角形和三维空间中的棱锥都称为“多边形”，其对应的距离都称为多边形距离，对应的维诺图都称为多边形维诺图。

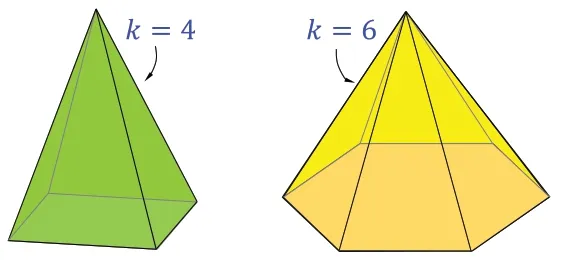
图4 k-棱锥示意图

根据定义可知，图3d中维诺胞元的边界是由站点集S中任意两点之间的多边形距离平分线组成，即所有到点p和点q的多边形距离dP相等的点的集合。值得注意的是，多边形距离平分线不是一条直线。在二维平面上，多边形距离平分线往往是由多条线段组成的折线；在三维空间中，则拓展为多边形距离平分面，同样由多个相交平面组成。三维空间中多边形距离平分面的定义如下：

图5所示为采用枚举法例举出的所有多边形（三角形）平分线的情况，同样可以看出n=3。其中，vi和ei(i=1,2,3)分别为多边形P的顶点和边。可以看出，三种情况下其多边形平分线均满足自支撑条件，即不存在悬垂的顶点，同时所有平分线与打印方向（y轴）的夹角都有ω≤ωmax。

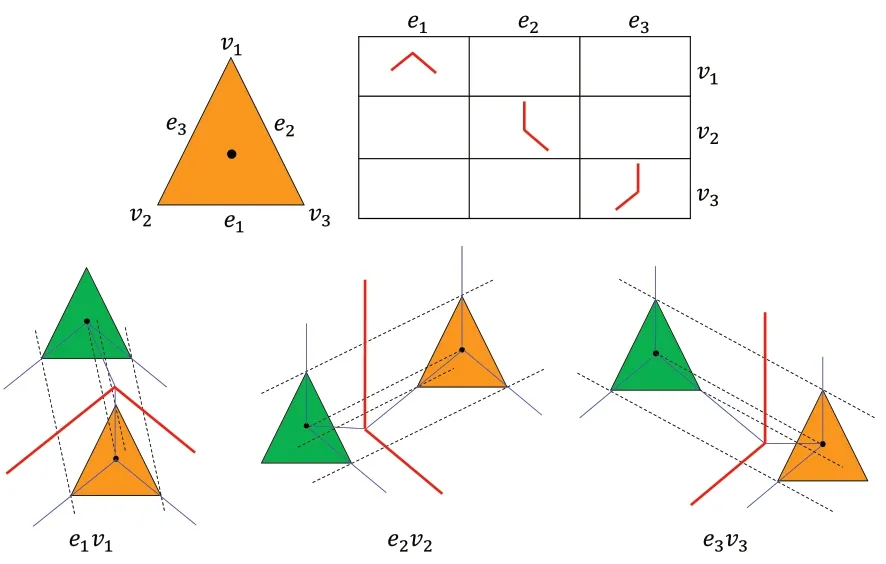
图5 多面形距离平分线满足自支撑条件

1.3 自支撑梯度多孔结构建模

梯度多孔结构的建模步骤如图6所示，其初始输入条件为站点密度场ρ={ρ1,ρ2,...,ρn}，其中ρi为单位体积内维诺站点的数量；ρi越大，对应的维诺胞元数量越多，力学性能越高。首先，采用站点随机采样算法将密度场ρ映射为设计模型内的站点分布，控制正交各向异性多孔结构力学性能的梯度分布；然后，采用切片算法对模型进行切片。对每一层切片，将其按一定分辨率离散为一系列体素，计算每个体素所属的维诺胞元，可以得到每一层切片的灰度图像。将所有切片层的绘图图像进行重构，可以输入.stl格式的模型；也可以直接将图像文件输入FDM打印机，直接打印成型。

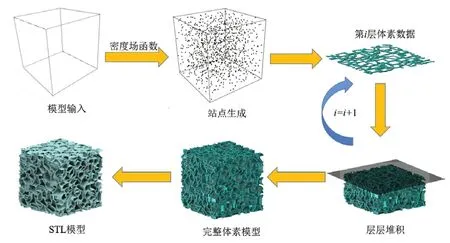
图6 多孔结构建模流程图

1.3.1 维诺站点随机采样

维诺站点分布是决定多孔结构梯度弹性分布的关键因素，本文采用基于隐式栅格的维诺站点生成算法，既能保证站点分布在宏观上符合输入的密度场，又能在微观上具有随机性。具体算法如下：

1）将模型离散为边长为a的立方体栅格；

2）遍历所有栅格，对当前栅格i，计算栅格i内的站点数量ti=a3ρi；

3）将栅格划分为8个子栅格，若ti≤8，则随机选取ti个子栅格，并分别在每个子栅格内部任意位置随机生成一个站点；反之，若ti＞8，则递归的对子栅格执行站点采集算法。

1.3.2 多边形维诺多孔结构生成

本文提出一种基于体素的多边形维诺多孔结构生成算法，如图7所示，将模型第i层切片离散为k×k个体素单元，计算每个体素所属的维诺胞元，每个体素均隶属于与其多边形距离最近的站点对应的维诺胞元。若体素与其相邻体素同属一个Voronoi胞元，则该体素位于Voronoi胞元内部，为空相；否则位于Voronoi胞元边界，为固相。

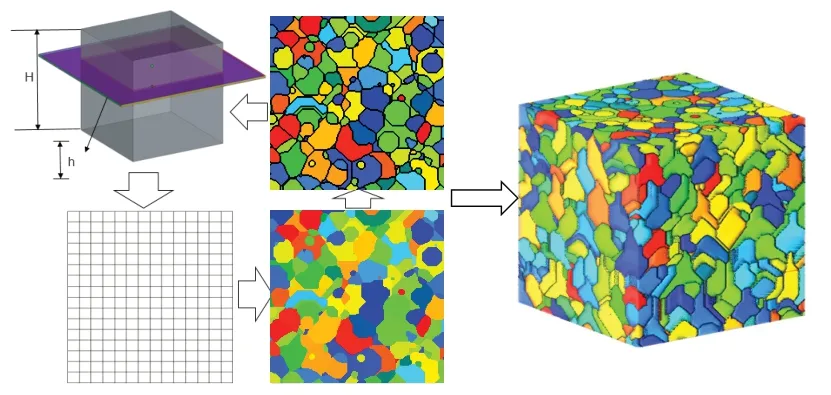
图7 三维多边形Voronoi图建模算法示意图

三维多边形Voronoi图生成算法步骤如表1所示。该算法的核心思想是在站点集合S中找到与体素i距离最近的站点s(i)；对于体素i，如果它的四个相邻体素的最近站点都为s(i)，则说明体素i位于Voronoi胞元内部，为空相部分；否则说明体素i位于Voronoi边界，为实体部分。

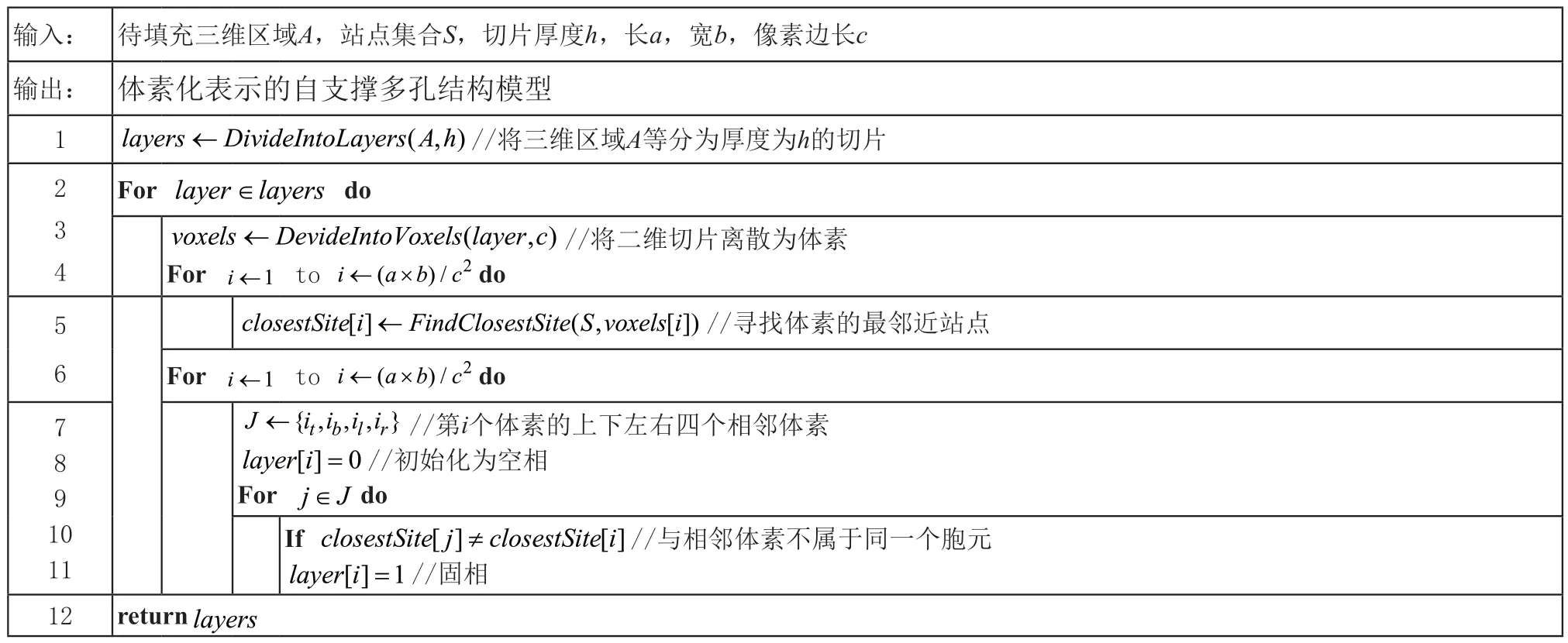
表1 三维多边形Voronoi图生成算法

1.4 几何结构的控制策略

本文采用图8所示几何设计参数控制棱锥的几何结构及其力学性能。由于棱锥的大小（等比例缩放）对最终生成的多孔结构没有影响，因此设原点O到棱锥底面的高度为1，棱锥顶点的坐标为(0,0,Az)；参数θ为过原点和底边的平面与底面的夹角，参数α为原点到侧面的距离ε与l的比值，可以求得棱锥顶点Az的计算公式为：

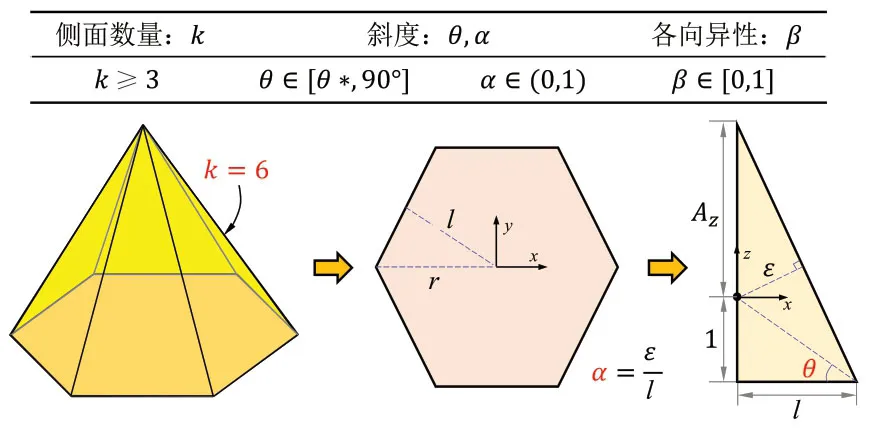
图8 棱锥的参数化

此外，通过将棱锥沿x方向收缩并以z轴为中心旋转，可以实现多边形Voronoi图的各向异性，参数β∈(1,0)为收缩因子，决定收缩的程度。

图9展示了各参数如何影响多边形Voronoi面的几何结构，图中心的样本参数为k=8，α=0.5，θ=45，β=1.0。其周围每个样本仅变化一个参数，每个样本左下方为其对应的棱锥。可以看出，参数k的变化对多孔结构几乎没有影响，而通过调整参数θ、α、β的大小，可以实现对多孔结构几何梯度的精确控制，具体如下：

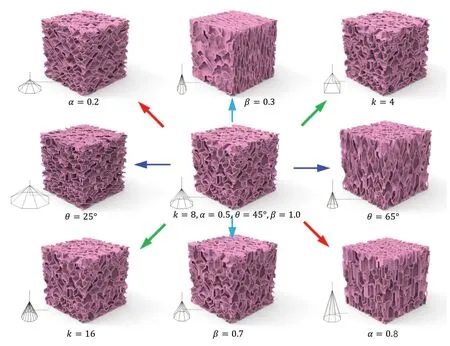
图9 多孔结构随参数变化示意图

1）参数θ决定了由棱锥生成的Voronoi面中倾斜面与水平面的夹角，当其他参数取值相同时，多孔结构中维诺面的斜率将随着参数θ的增大而增大。

2）参数α为棱锥侧面到原点的距离ε与底面中心到底面边的距离l的比值。随α减小，锥顶与原点的距离Az减小。图10展示了在二维空间中多边形维诺多孔结构随着α的变化规律，随着α减小，多维诺胞元的形状由垂直方向扁平状（正交各向异性）变化为非扁平状（各向同性）。

图10 α对多边形维诺图几何结构的影响

3）参数β为棱锥沿x方向的收缩因子。引入参数β使距离棱锥在某一方向上发生收缩，能够实现结构的正交各向异性。随着β的减小，Voronoi单元在x方向上趋于扁平。

2 多边形维诺多孔结构弹性性能分析

2.1 数值均质化

均质化是一种预测周期或近周期复合材料宏观特性的有效方法，广泛应用于材料性能分析与设计。其基本思想是用一种等效材料模型来替代复合材料。本文所提出的多边形维诺多孔结构虽然并不是周期性结构，但由于站点采集过程中使用的算法具有一定的随机性，因此，当多孔结构的尺寸比单个维诺胞元的尺寸大到一定程度时，可以看成具有近周期性。这种达到近周期性体积的多孔结构模型被称作代表性体积单元（Representative Volume Element，RVE），是数值均质化的分析对象。在弹性变形阶段，应力σ与应变ε关系如下：

其中，C是弹性矩阵，表征多孔结构的弹性行为。各向同性材料的弹性矩阵有弹性模量E和泊松比υ两个独立变量。数值均质化的本质是利用均质复合材料的各向同性性质来计算其弹性矩阵CH，根据均质化理论，CH计算公式为：

其中，k是刚度矩阵，f是等效节点载荷列阵。

2.2 弹性性能的控制策略

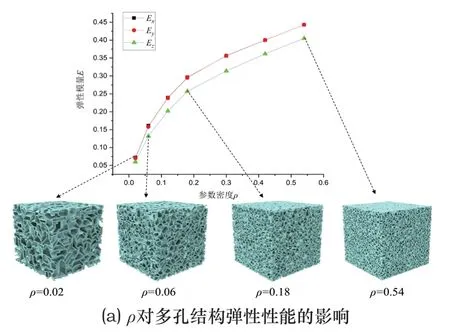
由第2.4小节可知，多边形维诺多孔结构的设计参数包括棱锥的几何参数如θ、α、β外，还包括输入的站点密度场ρ。为了研究上述设计参数对多孔结构弹性性能的控制规律，本小节以数值均质化方法为基础，采用控制变量法对各参数进行逐一分析，如图11所示。

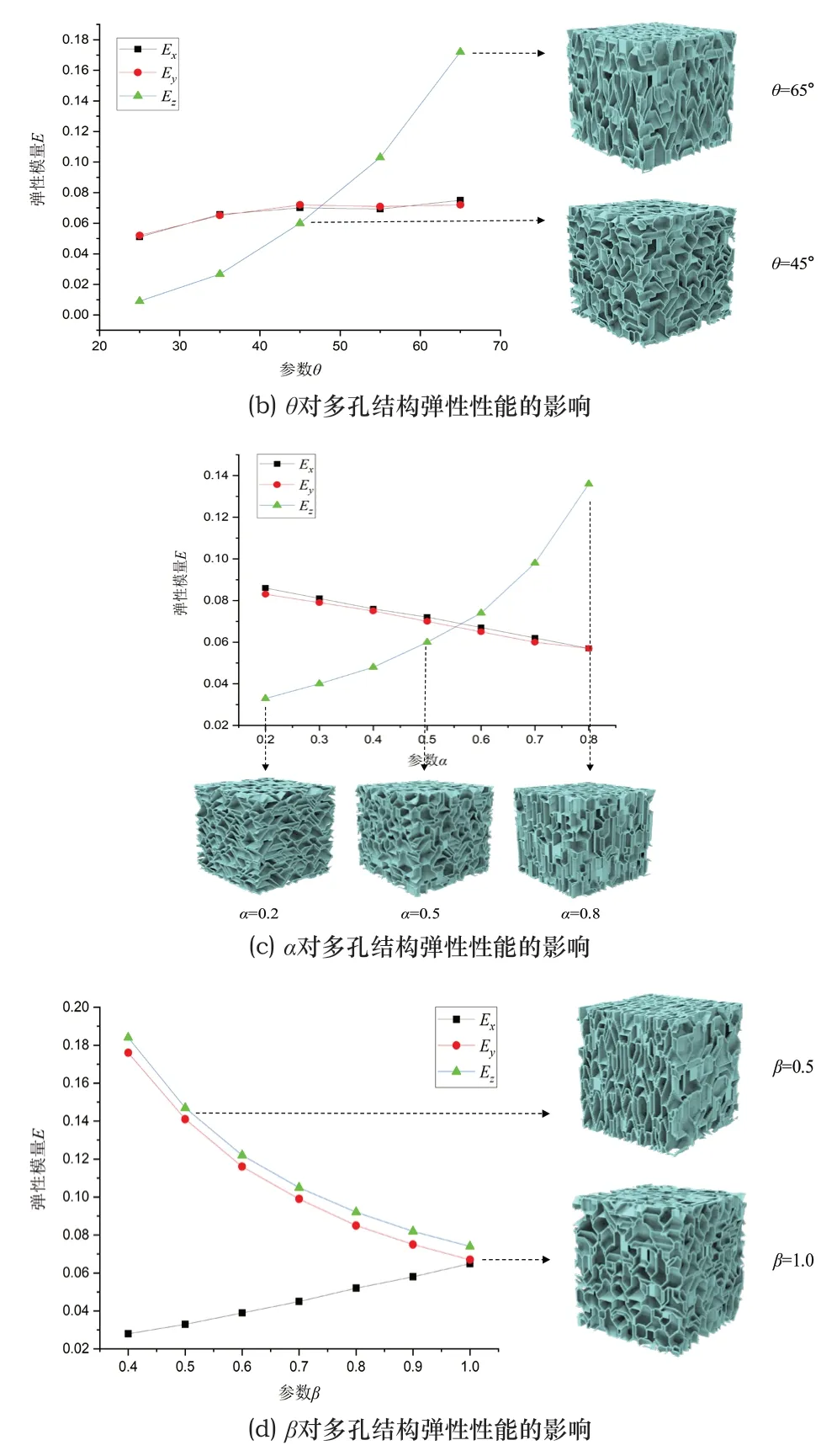
图11 设计参数对多边形维诺多孔结构的影响规律

1）站点密度ρ

图11(a)为固定参数θ=45°，α=0.5，β=1.0，k=4时，改变站点密度ρ的取值所对应维诺多孔结构分别在x、y和z方向的相对弹性模量（Ex、Ey、Ez）的变化曲线图。可以看出，三个方向的相对弹性模量均随着站点密度ρ的增大而增大。其原因在于：ρ越大，单位体积内站点数量越多，即维诺胞元的数量越多，孔隙率降低，相对体积分数增大，打印时消耗的材料也增多，因而在各方向上表现得更加坚固。

2）参数θ

图11(b)为固定参数ρ=0.02，α=0.5，β=1.0，k=4时，改变θ的取值所对应的维诺多孔结构Ex、Ey、Ez的变化曲线图。可以看出，θ增大主要导致Ez的增大，而对Ex、Ey影响较小。通过比较θ=45°和θ=65°的多孔结构，可以发现，随参数θ的增大，多孔结构的部分孔壁斜率增大，在整体上更接近竖直，致使多孔结构在竖直方向的相对弹性模量Ez增大。

3）参数α

图11(c)所示为固定参数ρ=0.02，θ=45°，β=1.0，k=4时，改变α的取值所对应的维诺多孔结构Ex、Ey、Ez的变化曲线图。可以看出，随着参数α的增大，Ez显著增大，而Ex和Ey逐渐减小。其原因可分析如下，由于参数α=ε/l，固定l，则随着α的增大，原点到侧面的距离ε增大，即棱锥的锥顶向上移动，侧面的面积增大，导致侧面与侧面之间生成的竖直孔壁占比增大，导致Ez增大。反之，当参数α减小时，棱锥的锥顶向下移动，侧面的面积减小，而底面始终不变，导致侧面与底面生成的斜率为θ的孔壁较侧面与侧面生成的竖直孔壁占比增大，使Ez减小。由于Az＞0，即锥顶始终在原点上方，故孔壁的斜率不会低于θ。

3 案例

本小节主要讨论梯度维诺多孔结构的应用情况，建模过程均采用Visual Studio 2013的MFC框架，搭配CUDA程序并行计算，在硬件环境为Inter Core2 i5-10400CPU，16GB内存与NVIDIA GeForce GTX 1650显卡的计算机上实现，最后通过FDM 3D打印机打印成型。

3.1 压缩实验

为严重本文多孔结构设计方法的有效性，建立了4组不同的立方体多孔结构模型，通过FDM 3D打印机打印成型，并进行压缩实验。打印的样品如图12(a)所示，包括1组各向同性多孔结构（包含2个样品，记作iso1和iso2）和3组不同方向的正交各向异性多孔结构（记作xoy1，xoy2，yoz1，yoz2，xyz1，xyz2）。模型尺寸为30×30×30 mm3，打印层厚为0.2mm，打印材料为PLA，打印速度为50mm/s。

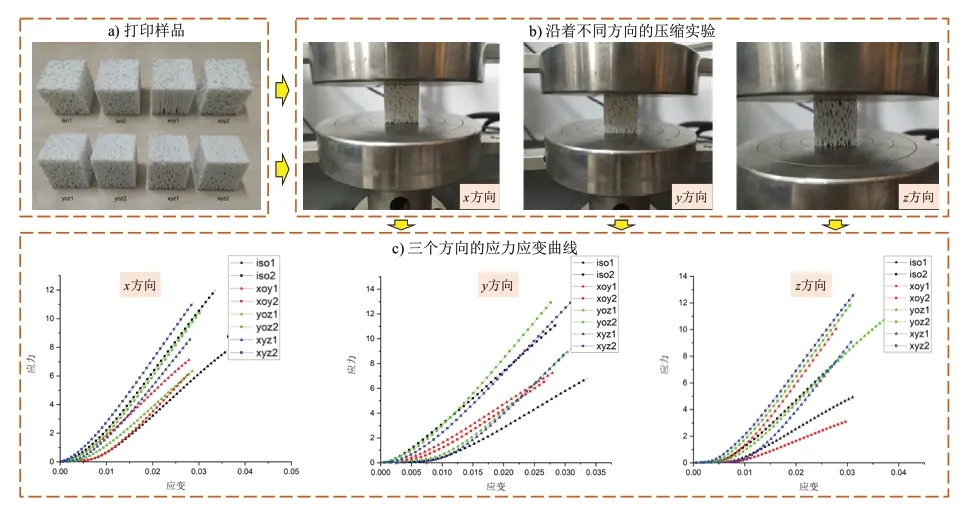
图12 压缩实验

对上述各样品进行x、y、z轴方向的压缩实验，实验设备为万测电子万能试验机TSE504D（图12(b)），压缩速度为0.5mm/min，可测的如图12(c)所示的应力应变曲线，并计算出样品的弹性模量Ee。为方便对比分析，需将真实弹性模量Ee按下式转换为相对弹性模量Er：

其中Ee为实验测得弹性模量，Eb为基体弹性模量，由基体试样压缩实验测得，Eb=851MPa。

此外，按照本文提出的数值均值化方法，也可以分析出设计的各模型分别在x、y、z轴向的相对弹性模量。将数字均质化结果和压缩试验结果进行对比，如表2所示。分别表示样本在三个方向的相对弹性模量，εx、εy和εz分别表示三个方向的相对误差。可以看出，实验结果和数值均质化结果在三个方向上的相对误差分别为8.14%，4.54%和9.29%，说明本文提出的多孔结构设计方法准确性较高。

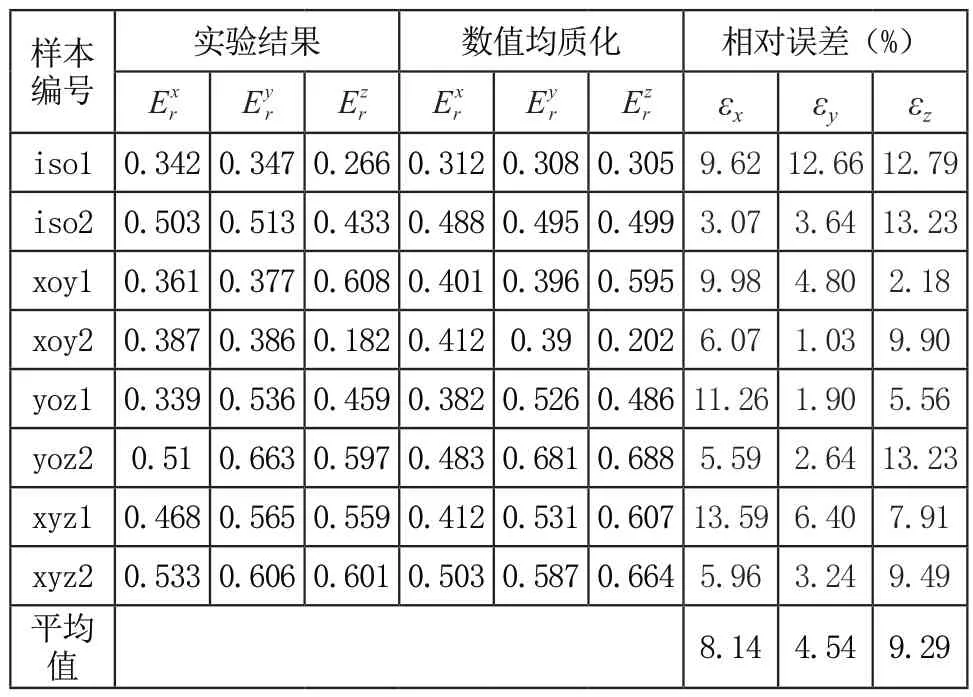
表2 压缩实验与数字均质化的结果对比

3.2 梯度多孔结构在鞋中底设计中的应用

本小节以足底压力为驱动，采用本文方法生成定制化的梯度多边形维诺多孔结构的鞋中底，使其不同区域的弹性模量按照足底压力大小分布，并采用PLA材料通过FDM 3D打印机进行打印，如图13所示。此外，本文还设计了各向同性的均质多边形维诺多孔结构鞋中底作作为对比。

图13 两种多边形维诺多孔结构鞋中底

为分析上述两种多孔结构鞋中底的性能，本文设计了静态足底压力实验，对足底各区域的压力进行采集。将压力传感器贴合在鞋中底的上表面，体重为75kg的被测人员静止站立在贴有压力传感器的鞋中底上，使用Tekscan足底压力测量系统采集静态站立时足底峰值压力，如图14所示。

图14 静态站立的足底峰值压力测量

为了更准确的获取足底压力数据，分别对两种鞋中底进行了5次重复实验，获得静态站立时足底峰值平均应力云图，并拟合出沿鞋中底长度方向的足底压力曲线如图15所示。

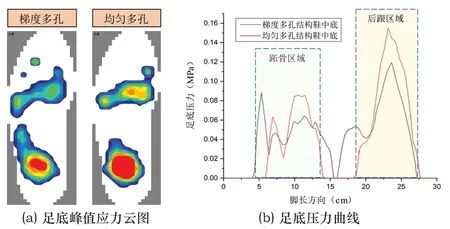
图15 足底压力实验结果

可以看出，足底受力较大的区域集中在跖骨区和后跟区；在跖骨区，虽然两种鞋中底受到的峰值压力基本相当，约为0.083MPa，但梯度多孔结构鞋中底在该区域的受力面积更大，说明受力更均匀；在后跟区域，均匀多孔结构鞋中底受到的峰值压力为0.156MPa，梯度多孔结构的鞋中底受到的峰值压力为0.122MPa，相比下降了21.8%。实验结果表面通过对鞋中底多孔结构进行梯度设计，能够有效降低静态站立时的峰值压力，从而调整足底压力分布，使鞋中底各区域受力更均匀，提升舒适性。

3.3 其他应用案例

图16(a)所示为左右两边具有不同梯度弹性的长方体，长方体中间部分为各向同性的过渡单元，左右两边各向异性方向旋转了90°，因此呈现出截然不同的弹性行为，即：左半部分可以轻易地弯曲，而右半部分却保持着较大的刚度；相反，当受到来自上下两个方向的按压时，右半部分容易被压缩，而左半部分则难以被压缩。图16(b)所示为手指模型，通过调整模型关节处维诺多孔结构的设计参数，可以使其在受力时仅在关节处发生弯曲，而其他部位不发生弯曲。图16(c)所示为两个径向具有不同弹性性能的圆环模型，左边的圆环能承受较大的径向载荷，而右边的圆环在承受径向载荷时容易发生变形。图16(d)所示为沿着轴线各向异性方向由0～90°连续变化的圆柱体，这种设计使其在轴向具有较大的刚度，不容易发生弯曲；而沿着各向异性变化方向扭转圆柱体时，能轻松地使其发生变形。

图16 其他应用案例

4 结语

本文提出了一种基于多边形维诺图的自支撑梯度弹性多孔结构设计方法，选择k-棱锥计算多边形距离，通过固空相判断算法生成模型每一个切片层的灰度图像，采用重构算法生成自支撑的维诺多孔结构。在此基础之上，对k-棱锥进行参数化表达，提取维诺多孔结构的关键设计参数。研究了基于设计参数的梯度维诺多孔结构的几何结构、弹性性能的控制策略。最后，基于数值均质化方法，探索了弹性梯度多孔结构的控制策略，并通过压缩实验证明了数值均质化方法的有效性。最后，本文还将所提出梯度多孔结构应用于鞋中底等物体的设计，结果表明：本文提出自支撑梯度弹性多孔结构设计方法设计简单、可控性高，通过调整设计参数，能够较为容易的设计出各向异性、各向同性或梯度弹性的多孔结构模型。