New soliton wave solutions of a (2+1)-dimensional Sawada-Kotera equation
Kon Dein Hdi Rezzdeh Nji Ullh Jvd Vhidi Klim U.Triq Lnre Akinyemi
a Department of Mathematics, Yantai Nanshan University, Shandong 265713, China
b Faculty of Engineering Technology,Amol University of Special Modern Technologies, Amol, Iran
c Department of Mathematics, COMSATS University Islamabad, Islamabad 45550, Pakistan
d Department of Applied Mathematics, Iran University of Science and Technology, Tehran, Iran
e Department of Mathematical Sciences, University of South Africa, Pretoria 0 0 02, South Africa
f Department of Mathematics, Mirpur University of Science and Technology, Mirpur 10250 (AJK), Pakistan
g Department of Mathematics, Lafayette College, Easton, Pennsylvania, United States
Keywords:Modified Kudryashov method Sardar-sub equation method Bäcklund transformation(2+1)-dimensional SKE Soliton wave solutions
ABSTRACT In this work,we studied a (2+1)-dimensional Sawada-Kotera equation (SKE).This model depicts nonlinear wave processes in shallow water,fluid dynamics,ion-acoustic waves in plasmas and other phenomena.A couple of well-established techniques,the Bäcklund transformation based on the modified Kudryashov method,and the Sardar-sub equation method are applied to obtain the soliton wave solution to the (2+1)-dimensional structure.To illustrate the behavior of the nonlinear model in an appealing fashion,a variety of travelling wave solutions are formed,such as contour,2D,and 3D plots.The proposed approaches are proved more convenient and dominant for getting analytical solutions and can also be implemented to a variety of physical models representing nonlinear wave phenomena.
1.Introduction
Nonlinear partial differential equations (NPDEs) have the key rule in many fields including nonlinear optics,elasticity theory,engineering,fluid dynamics and plasma physics;provide a crucial part for the modeling of real-world problems.The era of analytical solutions is becoming progressively more significant in a variety of regions of applied science and engineering.To have a better understanding for the nonlinear phenomena and its possible applications in everyday life,the travelling wave structures plays a dominant rule to realize the wave structures more efficiently.That’s why,the renowned researchers of this decade are more curious to develop some novel analytical solutions for such models.Solitons of NPDEs are vastly used in both fundamental theory and applications of nonlinear science.The soliton and solitary wave solutions provide physical information and improve the mathematical features of the problem [1–7].
Many researchers developed the standard NPDEs,their exact and multiple-soliton wave solutions due to some insight properties,dynamical behaviors,and nonlinear phenomena in nineteenth century.It was a difficult task to get some exact solutions analytically.But recently researchers proposed techniques to find the new exact-soliton solutions of NPDEs.These methods include the Kudryashov method [8,9],the Sardar-sub equation method[10,11],the auxiliary equation method [12,13],the extended Fan sub-equation method [14,15],the Lie symmetry analysis [16,17],the extended unified method [18,19],the (G′/G)-expansion method[20,21],the exp (-φ(ξ))-expansion method [22,23],and many more [24–58].
In literature,various researchers have studied this model analytically such as the lump solutions are developed for positive quadratic function solutions to the associated bilinear equation[59],the analytical rational solutions in terms of positive quadratic functions [60],the simplified form of Hirota’s bilinear method is employed to construct some multiple singular soliton solutions[61],the gage transformation along the New bilinear Bäcklund transformation with multi-soliton solutions [62].
As the modified Kudryashov method and Sardar-sub equation method are the soliton wave methods,so there will be some interaction between the inner-wave and the different frequency,velocity components.Soliton wave solutions are also called multiwave solutions.These can be converted into single soliton having too much energy propagating on high regions of space without any dispersion.At last,it becomes highly destructive wave.We use Bäcklund transformation based on modified Kudryashov method and Sardar-sub equation method for finding the new soliton wave solutions for (2+1)-dimensional SKE.
Ma et al.considered the following form of the (2+1)-dimensional SKE [63]
whereu=u(x,y,t) is an unknown function with spatial coordinatesxandyhaving the propagation direction,andtis referred as temporal coordinate.These coordinates have different aspects in mathematical physics.It specifies a region confined in both time and space.These coordinates enable us to specify a location in an image with better effect as compared to pixel coordinates.The SKE has various applications in the nonlinear evolution equation of long waves of relatively small amplitude in shallow water of uniform depth,Alfven waves in a plasma,nonlinear acoustic waves in an inharmonic lattice,and many other significant scientific phenomena.
This partition is as follows: in Section 2,some fundamental and useful features of the Bäcklund transformation based on modified Kudryashov method and Sardar-sub equation method are presented.In Section 3,we find the new soliton wave solutions of(2+1)-dimensional SKE Section 4.presents some graphical representation of the solutions.The conclusion is provided in the final section.
2.Description of methods
We consider a NPDE foru=u(x,y,t) in the form
We introduce the transformation
wherecis constant.Rewriting Eq.(2) in the following NODEs
where prime denotes the derivative with respect toη.
The key steps of the Bäcklund transformation based on modified Kudryashov method and Sardar-sub equation method are as:
2.1.The Bäcklund transformation based on modified Kudryashov method
Step 1.Suppose that the solution of Eq.(5) can be written in terms ofδ(η)as
where
andP,Qare arbitrary parameters andQnot equal to the constants 0,a0,a1,...,aN,which can be find later andϕ(η) is the new variablefollowing the given NODE:
Eq.(8) gives
wheredis an arbitrary parameter.Note that,Nis a positive integer can be find by the balancing principle in Eq.(5).
Step 2.Putting Eq.(6) in Eq.(5) and then equating to zero all the coefficients ofϕi(η),we get nonlinear algebraic system ina0,a1,...,aN, andc.
Step 3.Puttinga0,a1,...,aN,c, Eq.(9),and Eq.(7) into Eq.(6),we find soliton wave solutionsof Eq.(5).
2.2.The Sardar-sub equation method
Step 1.Suppose that the solution of Eq.(5) can be written in terms ofδ(η) as
wherea0,a1,...,aNwhcih can be find later and the new variableδ(η) will follow the given NODE
whereϖandρare real constants Eq.(11).gives
Case I:Ifϖ >0 andϑ=0, then
where
Case II:Ifϖ <0 andϑ=0, then
whereκandλare arbitrary parameters.Note thatNis a positive integer which can be found by the balancing principle in Eq.(5).
Step 2.Putting Eq.(10) into Eq.(5),and setting all the coefficients ofδi(η) to zero,we get nonlinear algebraic system ina0,a1,...,aN,ϖ, andc.
Step 3.Puttinga0,a1,...,aN,ϖ,c, and the solutions obtained from Eq.(11) into Eq.(10),we find soliton wave solutions of Eq.(5).
3.Solutions ofthe (2+1)-dimensional SKE
Now,we apply the Bäcklund transformation based on modified Kudryashov’s method and the Sardar-sub equation’s method to find the exact-soliton wave solutions for the (2+1)-dimensional SKE.Firstly,we let
Substituting Eq.(10) in Eq.(1),we obtain NODEs
By applying anti-derivative on Eq.(28) with respect toη, and then neglecting the constant of integration,we get
Substituting Eq.(29) into Eq.(27),after integrating with respect toη,whereBis constant of integration,we have
Balancinggηηηηandg3in Eq.(30),givesN=2.This gives a finite series as follows
wherea0,a1, anda2are constants can be find from the solution of Eq.(30).
3.1.The Bäcklund transformation based on modified Kudryashov method
Using Maple software gives the following two sets:
Set 1.
From Eqs.(32),(26),(9),(7),along with (31),we get the new type of soliton wave solution of the (2+1)-dimensional SKE as follows:
Set 2.
From Eqs.(33),(26),(9),(7) along with (31),we get the new type of soliton wave solution of the (2+1)-dimensional SKE as follows:
whereη=x+y+(ln2A(ln2A-15a0+1)+a0(45a0-6))t.
3.2.The Sardar-sub equation method
Using Maple software gives the following two sets
Set 1.
From Eqs.(34),(26),(31),along withthe solutions of Eq.(11),we get the new type of soliton wave solution of the (2+1)-dimensional SKE as follows:
From Eqs.(35),(26),(31) along withthe solutions of Eq.(11),we get the new type of soliton wave solution of the (2+1)-dimensional SKE as follows:
4.Graphical presentation
In mathematical physics,the spatial and temporal coordinates have different properties.In comparison to pixel coordinates,these coordinates allow us to identify a position in an image with greater effect.In the nonlinear evolution equation of long waves of relatively modest amplitude in shallow water of uniform depth,Alfven waves in a collisionless plasma,nonlinear acoustic waves in an inharmonic lattice,and many other relevant scientific phenomena,the SKE has many applications.
In this section,we plot the exact-soliton solutions for the(2+1)-dimensional SKE in Figs.1 -4.The physical interpretation of set of new wave solutions in Eq.(1) is given by using the Maple software for the better understanding to show the behavior of solitons for various parameters.In Fig.1,the soliton wave solution ofu1is plotted forP=1,Q=0.5,d=1.5,A=e,andy=1.In Fig.2,the soliton wave solution ofv2is plotted forb0=0.75,P=-1,Q=1.5,d=1.5,A=2.6, andy=1.In Fig.3,the soliton wave solution ofu7is plotted forb0=-0.4,κ=1.1,λ=1.05,andy=1.In Fig.4,the soliton wave solution ofu7is plotted forb0=0.5,ϖ=1.5,κ=0.9,λ=0.95, andy=1.The interval in all the cases is within -10≤t,x≤10.

Fig.1. The plots in 3D,contour,and 2D respectively of the modulus of the soliton wave solution of u1,when P=1,Q=0.5,d=1.5,A=e,y=1, within the interval -10≤t,x≤10.

Fig.2. The plots in 3D,contour,and 2D of the modulus of the soliton wave solution of v2,when b0=0 .75,P=-1, Q=1.5 , d=1.5, A=2.6, y=1, within the interval-10≤t, x≤10.

Fig.3. The plots in 3D,contour,and 2D of the modulus of the soliton wave solution of v17,when b0=-0.4, κ=1.1, λ=1.05, y=1, within the interval -10≤t,x≤10.
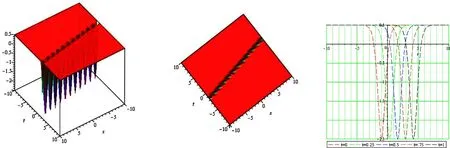
Fig.4. The plots in 3D,contour,and 2D of the modulus of the soliton wave solution of v7,when b0=0 .5, ϖ=1.5, κ=0.9, λ=0.95, y=1, within the interval -10≤t,x≤10.
5.Conclusion
A (2+1)-dimensional SKE was used to derive a new completely integrable equation.The new soliton wave solutions were obtained by using the Bäcklund transformation based on modified Kudryashov method and Sardar-sub equation method.These solutions include exact-soliton solutions.They are the well-known techniques to handle nonlinear dispersive equations of any order.Also,the Bäcklund transformation based on modified Kudryashov method and Sardar-sub equation method give soliton wave solutions for completely integrable equations.The findings of this study demonstrate that the offered methods are effective techniques for obtaining novel exact solutions to nonlinear evolution equations.Furthermore,using the most up-to-date scientific methods,the nature of the solutions would be presented in three dimensions for various parameters.With the help of 3D,contour,and 2D illustrations,the physical behavior of the solutions is graphically depicted,for details see Figures (1–4).
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
 Journal of Ocean Engineering and Science2023年5期
Journal of Ocean Engineering and Science2023年5期
- Journal of Ocean Engineering and Science的其它文章
- New solitary waves and exact solutions for the fifth-order nonlinear wave equation using two integration techniques
- Numerical treatment of temporal-fractional porous medium model occurring in fractured media
- Optimal Kalman-like filter for a class of nonlinear stochastic systems
- Dynamic quantitative risk assessment of LNG bunkering SIMOPs based on Bayesian network
- Review of enhancement for ocean thermal energy conversion system
- Prediction of residual tensile strength of glass fiber reinforced polymer bars in harsh alkaline concrete environment using fuzzy metaheuristic models
