求解带有混合约束的极大极小优化问题的神经网络方法

沈 洁, 解昱菲, 郑欣蕾

(辽宁师范大学 数学学院,辽宁 大连 116081)

极大极小优化问题在电路设计、管理科学及经济学等许多领域有广泛应用. 由于极大极小优化问题的目标函数不可微,因此有两个解决问题的方向,一种是用非光滑函数的次梯度生成目标函数的割平面近似模型,这种方法虽然模型清晰,但在计算次梯度时,往往会遇到较大困难. 另一种方法是通过引入变量将极大极小优化问题进行光滑化处理,再利用经典的优化方法,如线搜索算法、信赖域算法和罚函数法等进行求解,如文献[1]中借助半罚函数思想,提出了一个广义投影算法,该算法的特点是,由一个广义梯度投影显式公式产生的搜索方向是下降可行的,并构造了一个最优识别控制函数. 但这种算法在计算时间上极度依赖问题的维数、结构和算法的复杂度,因此求解高维或结构复杂的优化问题需要更好的方法. 本文通过构建神经网络求解极大极小非光滑优化问题, 首先利用最大熵函数近似非光滑的目标函数,将问题转化为光滑优化问题,再构建用常微分方程刻画的动态系统(递归神经网络). 理论分析证明了动态系统的解轨线收敛到优化问题的近似最优解. 最后给出的数值实验证明了所构造递归神经网络求极大极小问题的有效性.

1 预备知识

考虑下述极大极小问题:

(1)

其中,x∈n,X={x∈n|l≤x≤h},l=(l1,l2,…,ln)T,h=(h1,h2,…,hn)T.fi(x),gk(x)是二次连续可微凸函数,A∈r×n,rank(A)=r,b∈r.记Ξ={x∈n|gk(x)≤0,k=1,2,…,m,Ax=b,x∈X},尽管fi(x)(i=1,2,…,s)都是连续可微函数,但是目标函数是非光滑函数.

假设1(i)问题(1)的最优解存在;

下面给出如下最大熵函数[1]:

(2)

最大熵函数fp(x)是一个光滑函数,它具有如下良好的性质.

引理1[2](i)随着p趋于无穷,fp(x)逐点收敛到f(x).

(ii)随着p趋于无穷,fp(x)一致收敛到f(x).

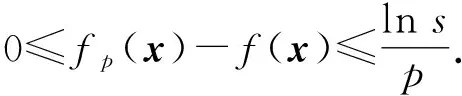
(iv)如果每个fi(x)(i=1,2,…,s)在凸集Ξ上都是凸函数,那么fp(x)也是凸函数.

根据上面熵函数的性质,可以将原问题(1)近似为下面的光滑凸优化问题:

(3)

其中,g(x)=(g1(x),g2(x),…,gm(x))T,fp(x),gk(x)(k=1,2,…,m)都是二次连续可微凸函数.

光滑熵函数fp(x)能够很好地近似原问题(1)中的非光滑函数f(x),因此光滑凸优化问题(3)的最优解是原问题(1)的近似最优解,而且p越大,近似效果越好. 所以只需求解近似问题(3)就能得到原问题的近似最优解.根据最优性条件[3],知道,x*是问题(3)的最优解当且仅当对任意的x∈Ξ,有(x-x*)T∇fp(x)≥0,其中,∇fp(x)表示fp(x)的梯度.

定理1[4]设Ω⊆n是非空闭凸集,x*∈Ω,F:Ω→n为连续映射,则x*满足变分不等式(x-x*)TF(x*)≥0,∀x∈Ω的充要条件是x*满足投影方程-x*+PΩ(x*-F(x*))=0.

2 投影神经网络模型构建

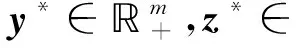
其中,∇g(x)=(∇g1(x),∇g2(x),…,∇gm(x))T表示g(x)的Jacobian矩阵.

为了求解近似问题(3),构建如下递归神经网络模型:

(4)

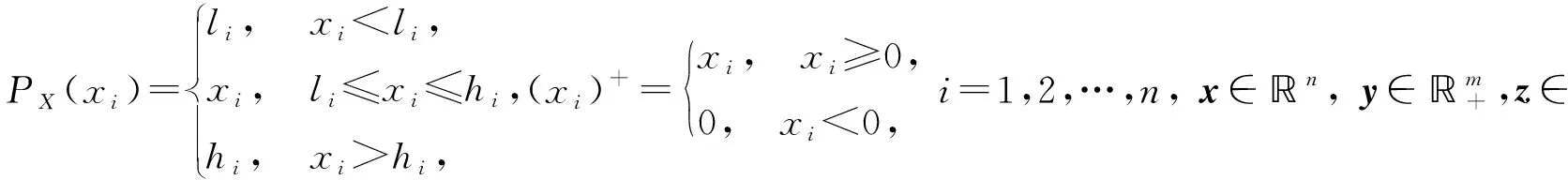
3 稳定性与收敛性分析

这里主要采用文献[6-7]中的方法讨论神经网络(4)的稳定性和收敛性.

引理2(i)神经网络(4)至少存在一个平衡点.如果(x*,y*,z*)是神经网络(4)的平衡点,那么x*是问题(3)的最优解.

(ii)对任意初始点,神经网络(4)存在唯一的连续解.

(iii)设u(t)=(x(t),y(t),z(t))是神经网络(4)的带有初值u(t0)=(x(t0),y(t0),z(t0))的解轨线,如果x(t0)∈X且y(t0)≥0,那么有x(t)∈X和y(t)≥0.下面具体分析构建的神经网络(4)的稳定性和收敛性.

定理2假设∇2fp(x)在Ξ上是正定矩阵,那么带有初值u(t0)=(x(t0),y(t0),z(t0))的神经网络(4)在Lyapunov意义下是稳定的,而且x(t)指数收敛到问题(3)的最优解x*.

考虑下面的Lyapunov函数:

其中,u*=(x*,y*,z*)是神经网络(4)的平衡点,且

又因为投影不等式[6]:

(v-PΩ(v))T(PΩ(v)-u)≥0,∀v∈n+m+r,u∈Ω,

-G(u)T{PΩ(u-G(u))-u}≥‖PΩ(u-G(u))-u‖2.

注意到T(u)=PΩ(u-G(u))-u,则

O1∈n×m,O2∈n×r,O3∈r×m,O4∈r×r是零矩阵. 注意到yi≥0,∇2gi(x)是半正定的,那么∇G(u)也是半正定的,且T(u)T∇G(u)T(u)≥0,因此得到

G(u)T(u-u*)≥(G(u)-G(u*))T(u-u*),

因此

一方面,有

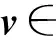
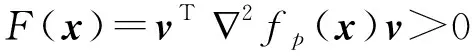
由于问题(3)是极大极小问题(1)的近似问题,因此神经网络(4)指数收敛到极大极小问题(1)的近似最优解.

4 数值实验

考虑如下极大极小优化问题:

该问题最优解为x*=(1.1390,0.8996)T. 令

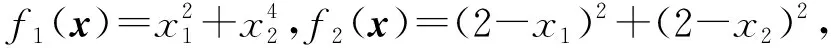
数值结果表明神经网络(4)的解轨线收敛到其平衡点x*=(1.1378,0.8998)T. 图1显示了带有6个不同初始点的基于神经网络(4)的解轨线x(t),从图中可以看出6条解轨线均收敛到近似问题的平衡点,也就是原问题的近似解(1.1378,0.8998)T. 该数值实验表明,应用本文提出的递归神经网络可以得到极大极小优化问题的近似最优解.

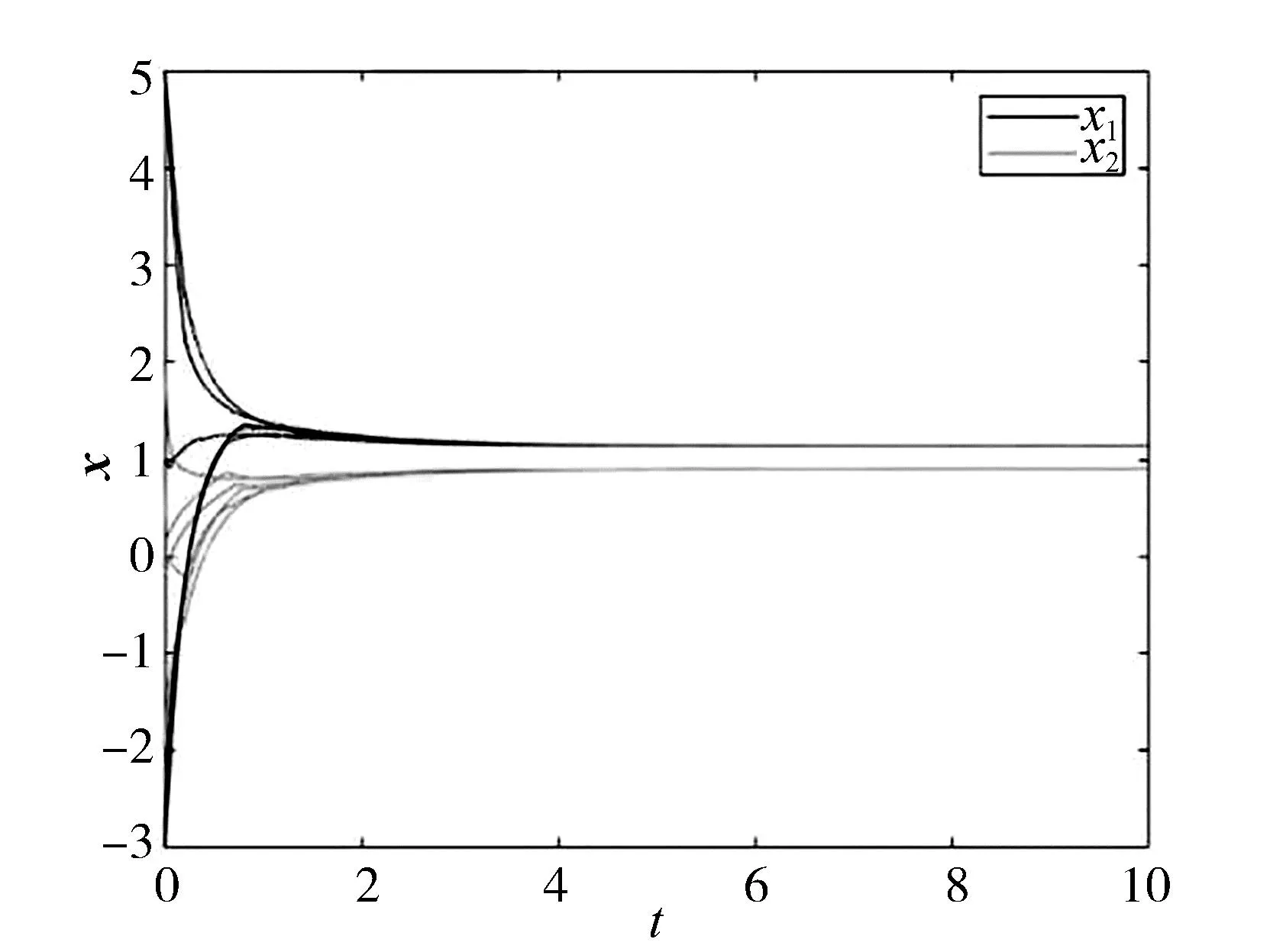
图1 神经网络的解轨线Fig.1 The trajectories of neural network