竖直周期外驱力下的颗粒碰撞自组织研究

赵梓茗,王 伟,周路群

(北京大学 物理学院,北京 100871)

颗粒物质在生产生活中普遍存在,但是由于这类物质的能量耗散不可忽略,无法用力学方法预测,从而导致很难给出理论上的解析解. 同时,颗粒系统有着不同于固体和流体的动力学性质,因此常常表现出一些反常效应.

竖直外力驱动的颗粒碰撞行为,也被称为“沙堆麦克斯韦妖效应”,是揭示颗粒系统奇特动力学性质最经典的实验. 1996年,Schlichting等人提出了类似的演示实验[1],并且被Eggers在1999年提出的二维圆盘碰撞模型进行定性解释[2]. 然而Eggers没有给出粒子数在竖直方向的分布,理论计算得到的等效温度也与实验结果不符合. 因此本文建立了颗粒碰撞的三维模型并且定量计算相关参量,实验结果与理论符合较好.

1 实验装置和现象

实验装置如图1所示,采用上端开口的透明容器(5 cm×2 cm×15 cm),用竖直金属隔板将容器等分为2个腔室,只在隔板距离容器底1 cm处开有高度为3 mm的水平狭缝,允许两腔室内的粒子交换. 采用扫频信号发生器产生可调频率输出,经功率放大器驱动激振器. 激振器通过磁线圈的电信号驱动电机顶杆,推动振动台上下周期运动,再通过压电加速度传感器将其转换为电信号,由电荷放大器放大后显示在示波器上.

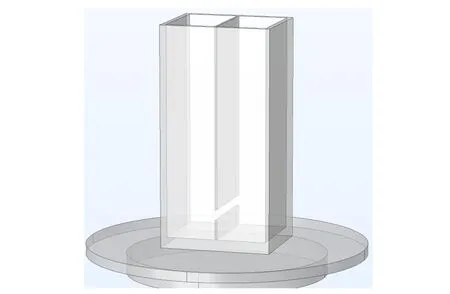
图1 实验装置示意图

实验开始前,在容器一侧放入460粒直径为1 mm的铜球. 将容器固定在振动台上,施加振幅变化、频率为50 Hz的三角波电压. 观察到粒子在容器中四处碰撞、上下振动,如图2(a)所示. 部分粒子从狭缝转移到另一腔室,两侧粒子数在几分钟内达到稳定,系统进入振动平衡状态,如图2(b)所示. 这时关闭电源,振动停止,两腔室中的粒子分别落在各自腔室的底部,不再交换. 统计振动平衡时两侧腔室内铜球的数量.

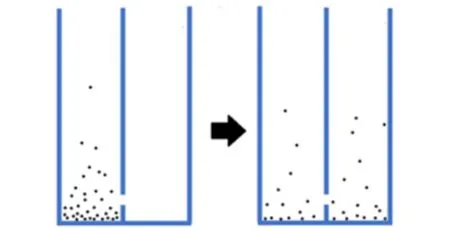
(a)刚开始振动 (b)振动平衡图2 容器内粒子状态示意图

实验中观察到,保持粒子总数、种类和振动频率不变,若振幅大于某阈值A0,则平衡后两腔室的粒子数基本一致,如图3(b)所示. 反之,若振幅小于该阈值,则平衡时两腔室的粒子数不相等,且振幅越小,两腔室的粒子数差异越大,如图3(c)所示.

(a)实验开始前

在以往的实验中,一般采取改变频率而保持振幅的方法[1]. 出于测量原理考虑,本文在实验中保持频率不变而调节振幅. 由于最大加速度正比于振幅,通过简单计算可以得到两腔室的球数量比与振幅的关系.

2 理论建模和计算

在实验中,所有运动过程均依靠粒子碰撞完成,因此可以观察到重力作用下粒子数密度下高上低的特点.

在恢复系数e比较大的情况下,由于单次碰撞能量损失δE∝1-e2,因此可以将粒子数密度n≫1和1-e≪1的微观化气体进行类比,并保持单位体积碰撞能损功率n2(1-e2)不变,这就要求选取数量大而弹性好的刚性小球作为实验材料,本文选取铜球.

(1)

以上4式来源于理想气体物态、受力平衡、碰撞频率和传热方程.式中,变量p和Q为粒子等效压强和单位面积传热功率;σ,κ和〈E〉分别为粒子碰撞截面、导热系数和单次平均能量损失.由近平衡碰撞理论,可以计算得到:

(2)

(3)

以上计算过程采用相对运动粒子对心连线方向上相对速度分布服从T=2T0的麦克斯韦速率分布这一结论[3].

将式(2)～(3)代入式(1),得到:

(4)

对于将颗粒系统近似为理想气体的研究,方程组(4)是精确的,但难以求出解析解.

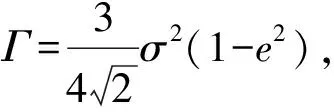
(5)

将方程组(5)代入式(1),得关于y的微分方程为

(6)

虽然解析方程(6)并不初等,但后文的研究表明在适当的近似条件下,模型结果与实验测量符合较好.

(7)

考虑到温度的物理意义,y应在任何位置不发散,因此必有T为常量.代入某高度单位厚度的能量损耗功率方程(4),可以求得总损耗功率为

(8)

(9)

其中,S为每个腔室的底面积,式(8)利用了归一化条件.

计算高度z=0处由底板振动带来的能流密度,与总损耗功率相当.由于系统总体受力平衡,因此底面的压力大小始终为F=mgN(N为粒子总数).设底板上移时速度为V,则等效压力f=2mgN,驱动功率U=mgNV.由于系统的消耗功率Q和驱动功率U相同,因此将式(9)变形即可算出温度为

(10)

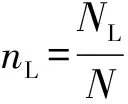
(11)

将式(10)代入式(11)可得到:

(12)

其中,A为振幅,f为三角波电压的频率,h为狭缝到容器底部的高度.

最终稳定振动时左右两侧腔室向对方转移的粒子数应相等,即PL=PR,用nL和nR表示为

(13)

为求解方程(13),将其两侧所代表的曲线作图,如图4所示.改变序参量γη的值,得到方程解的特征也不同.

(a)γη=3.2

从图4可以看出,方程(13)存在2种解:

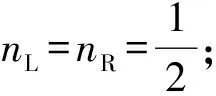
2)只有在γη>4的条件下才会出现的非对称解.理论计算中,非对称解的值随序参量γη的变化如图5所示.

图5 非对称解随序参量γη的变化

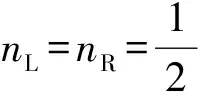
3 实验结果

固定频率f=60 Hz,用高速摄像机对振动台振幅做定标处理,得到关系系数k=72 V/mm.通过改变输入电压改变振幅,测量振幅A、参量η、粒子分布参量τ和理论指数τ0数据如表1所示.如果理论合理,则分布参量τ应当能拟合在图5的曲线上,使用最小二乘法回归得到系数γ=0.073±0.006,r=0.96.实验值与理论值γ0=0.069±0.004基本一致,可认为理论模型合理,本文计算了真实条件下的分布,结果令人信服[4].

表1 A,η,τ,τ0的测量数据

4 模型修正

显然,由于Γ不严格为0,前文对于方程(4)的近似不合理,也与测量结果不符. 但是,数密度n却有了良好的表达式,且与实验吻合. 下面将求修正解,优化对T(z)的描述.

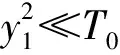
(14)

将式(14)代入微分方程(1),忽略高阶项,可得

(15)

此处选取实验参量.可判断exp (-λz)≪1确实成立,保留到一阶合理.利用y的表达式展开T,同时将y代入关于n2的表达式,可得

(16)

(17)

此处体现选择近似的意义:关于数密度n2的方程必须在T的一阶近似下才有意义.若取T=T0近似,则解得n2=0.这是因为Γ是一阶小量,必须将T的表达式也近似到一阶,否则就不能反映Γ的大小.而采用级数修正的意义正是能够在不改变n2表达式的条件下修正对T的描述.此时,方程(1)式近似成立的条件是:

(18)

可知,一阶修正的大小与Γ成正比.理想气体近似下,1-e2=0,Γ=0.对于e≠1的情况,则必须将指数按1-e2的阶数展开.而在本实验的参量选择下,计算表明展开到一阶就已足够准确.

为显示一阶近似修正的成功之处,将未修正结果(划线)、修正结果(点线)和测量得到的等效温度分布[5](实线)进行对比,如图6所示,可以看到引入一阶修正后对温度的描述更好.

图6 温度修正图

另一种可能存在的误差,是对底面单位时间传递热量的估计不准确.选择另一种求解观点,认为z=0位置的气体服从麦克斯韦速度分布规律,重新统计碰撞前后气体粒子能量的增量,通过积分计算得到:

mnv0T(0)=mgNv0,

(19)

5 展望和深入研究

在理解单种粒子的颗粒碰撞现象后,可以将类似的观点和处理方式运用在其他颗粒动力学现象中,例如坚果效应和逆坚果效应[6].在电场的胶体电泳、混悬液沉降问题中,类似的能量损耗也会发生[7].本研究的思路可以为这些有现实意义的问题提供帮助,特别是对于能量损耗小、数密度大的气相和液相体系(如混悬液、胶体、层析等),按损耗系数1-e2的阶数展开的修正方法具有参考意义.如何在这些体系中描述物理过程,是未来的研究方向.

6 结束语

本文基于热力学输运和逐级展开研究了受竖直驱动的颗粒系统的碰撞,展示了对颗粒系统的的研究思路:输运过程依靠粒子的剧烈碰撞实现,可以认为粒子服从理想气体状态方程和麦克斯韦速度分布. 为各向同性的粒子定义温度和热流,通过粒子运动输运能量传递损耗,计算粒子和温度分布. 本文将以往研究中定性的计算定量化,从热力学输运的角度近似,精确求出粒子分布的表达形式,并对文献[4]中没有指明的恒温近似做进一步处理,给出温度分布方程和一阶修正,证明该近似在实验条件下成立,同时与实验测量结果吻合.