基于杆系离散元理论的结构屈曲显式弧长法研究

叶继红，许 强

(1.中国矿业大学江苏省土木工程环境灾变与结构可靠性重点实验室，江苏，徐州 221116；2.中国矿业大学徐州市工程结构火灾安全重点实验室，江苏，徐州 221116)

有限元分析方法中，结构的屈曲现象一般作为几何非线性问题处理[1-3]，其荷载-位移曲线具有“位移跳跃”(snap-through)或“荷载跌落”(snap-back)显著特征，传统的分级加载模式无法顺利越过临界点。为此，RIKS[4]和CRISFIELD[5]提出了隐式弧长法，通过引入弧长约束方程实现“自适应”加载目的，成功捕捉结构完整的屈曲路径。HUANG 等[6]采用隐式弧长法捕捉了双曲复合壳体的卡扣现象。PAN 和LIANG[7]基于隐式弧长法研究了风梁等加固装置对储罐薄壁结构屈曲行为的影响。但在隐式算法中需要不断地集成和修正切线刚度矩阵，在临界点附近刚度矩阵出现病态甚至奇异。RAMESH 等[8-10]将柱面弧长法与动力松弛法(DRM)结合，提出了一种显式弧长法，由于不涉及刚度矩阵的集成、求解，更具稳定性，得到了广泛的应用与发展。ZU 等[11-12]基于显式弧长法对索杆张力结构成型过程进行了数值模拟。张鹏飞等[13]将有限质点法与显式弧长法结合，对薄壳屈曲问题进行了研究。ZHANG 等[14]采用显式弧长法对壳与杆系结构进行了屈曲分析。LEE 等[15-16]在显式弧长法中引入动力学阻尼，并采用对角刚度替换控制方程中的真实质量，简化了计算过程，提高了算法的稳定性与收敛速度。

与有限元法不同，传统离散元法是一种非连续介质力学方法，最初主要应用于研究岩石等非连续介质的力学行为，因其适合处理大变形、大位移等强非线性问题，所以被逐步引入到结构工程领域。基于此，叶继红教授课题组率先提出杆系离散元法(member discrete element method，MDEM)[17]，并成功将其应用于连续介质问题。该法将杆件离散为有限的刚性球颗粒，相邻颗粒间通过接触本构模型联接，然后采用牛顿第二定律确定各颗粒的空间坐标，并以颗粒的空间位置描述结构的空间位置和几何构型。杆系离散元不仅扩大了传统离散元的适用范围，同时保持了传统离散元法无需组集整体刚度矩阵和迭代求解运动方程的优势。目前已成功用于杆系结构的几何非线性行为[18-19]、材料非线性行为[20-21]、半刚性连接[22-23]、非线性动力响应[24-26]、屈曲行为[27]、网壳倒塌破坏模拟中[28-31]。上述研究成果表明，杆系离散元法在模拟结构非线性以及断裂倒塌等复杂行为中具有独特优势，是一种简单而有效的方法。

本文在杆系离散元理论的基础上，建立了一种显式弧长法以追踪结构屈曲平衡路径。该方法无需组集刚度矩阵，求解时不需要刻意区分结构是小变形还是大变形行为，与传统有限元方法相比更具优越性。首先介绍了杆系离散元的基本理论；其次，建立了新型接触单元—铰固接触的本构模型，分别采用离散元法和结构力学方法对铰固接触单元在已知端部位移工况下进行受力分析，然后通过端部内力相等建立方程，确定了接触弹簧刚度系数；再者，利用动力阻尼技术获取结构的准静态阻尼运动，大大简化了颗粒运动方程的求解过程，然后引入总位移约束弧长法，并详细介绍了与离散元法相结合的求解策略和实施过程；最后通过算例验证了该方法对结构屈曲分析的准确性和适用性。

1 杆系离散元法基本方程及内力求解

1.1 颗粒运动方程

杆系离散元法将结构离散为若干球颗粒的集合，如图1(a)所示，相邻颗粒间(如颗粒A 和B)则通过虚拟的零长度弹簧系统进行联接，并形成离散元法的基本分析单元-接触单元，如图1(b)所示。在任意时刻t，杆系离散元模型中所有颗粒的运动均满足牛顿第二定律，每个颗粒的运动控制方程具体形式为：

图1 杆系离散元分析模型Fig.1 Member discrete element analysis model

式中：at、vt分别为t时刻颗粒的加速度和速度矢量，包含3 个平动和3 个转动；M和C分别为颗粒的等效质量矩阵和阻尼矩阵；Pt和Ft分别为颗粒质心所受外力和内力，其中内力Ft由接触内力通过力系平移定理计算得到。

假定在每时间步Δt内速度是线性变化的，由中心差分法，可得t时刻颗粒的速度和加速度为：

将式(2)代入式(1)，得到颗粒在t+Δt/2 时刻的速度为：

式中，Rt=Pt-Ft为不平衡力。

1.2 接触单元的内力计算

要获取图1 中各颗粒的内力，需先求出相邻颗粒间接触点(如接触点C)的内力，然后通过力平移定理，反向叠加到相邻颗粒(如颗粒A 和B)上。对于线弹性体系，接触点C处的内力增量可由接触本构关系计算[22]，其表达式为：

式中：Δf为接触点处虚拟零长度弹簧系统的内力增量；K为接触单元的弹性刚度矩阵；Δd为局部坐标系下虚拟零长度弹簧系统两端结点的位移增量。

2 接触本构模型

离散元的核心问题是式(4)中接触刚度系数的求解。文献[17]基于简单梁理论，通过应变能等效推导出适用于“梁单元”的接触刚度计算公式。但桁架结构较为特殊，如图2 所示，杆件之间为铰接，在节点处形成的接触单元(以下简称铰固接触单元)，其特征为一颗粒固接、一颗粒铰接，与两颗粒固接的梁接触单元运动特性具有显著区别。

图2 二杆桁架结构及其离散元分析模型Fig.2 Two-bar truss structure and DEM analysis model

为确定铰固接触单元刚度系数，本文分别采用离散元法和结构力学方法对铰固接触单元在已知端部位移工况下进行受力分析，并通过端部内力相等建立方程，直接建立非连续介质方法与连续介质问题之间的联系。

因铰固接触单元自身运动的特殊性，对其提出以下三点假定：

1) 铰端颗粒上的接触点及两颗粒球心三点共线(运动假定)。

在离散元法中，接触弹簧位移由接触点对描述，其值由两颗粒相对运动关系确定。如图3 所示，初始时，接触点3、4 重合并分别在两颗粒边上，当两颗粒运动时，接触点对(3、4)发生相对位移，考虑铰节点处的颗粒1 可自由转动，本文在确定接触点对相对位移大小时，假定铰接颗粒上的接触点(3)和两颗粒球心(1、2)三点共线。

图3 铰固单元的受力分析Fig.3 Force analysis of hinged-fixed elements

2) 转动刚度为0(铰节点可自由转动)。

3) 利用力系平移定理将接触力移至两颗粒质心时，在铰接颗粒上产生的附加弯矩由固端颗粒承担(铰固单元整体受力平衡)。

在离散元法中，单元的力平衡条件被转化为两刚体接触处作用力与反作用力的相互作用，将接触力移至颗粒质心时，会在质心处产生附加弯矩，由于铰接处的颗粒不能承受弯矩作用，因此，从单元整体受力平衡的角度考虑，将铰接颗粒质心处产生的附加弯矩移至固端，由固端颗粒承担。

由于弹簧系统中的弹簧相互独立，互不耦合，在确定切向刚度系数kτ时，为直观起见，基于上述3 点假定，对图3 平面铰固单元在已知端部位移工况下进行受力分析。

对于图3(a)中的离散元模型，采用离散元法计算的端部内力为：

式中：M11、M22分别为接触力在颗粒1 和颗粒2 球心处产生的等效弯矩。

对于图3(a)中的有限元模型，采用结构力学方法[32]计算的端部内力为：

令式(5)与式(6)计算的端部内力相等建立方程，即：

求得切向刚度为：

同理，对于图3(b)，可求得切向刚度kτ=6EI/L3。

由于铰固接触单元拉压行为与结构力学中杆件的拉压行为一致，因此其轴向刚度系数与结构力学中杆件轴向刚度相同，即kn=EA/L。

引申至三维空间时，铰固接触单元的刚度系数矩阵为：

值得注意的是，采用上述方法求得梁接触单元刚度系数与文献[17]相同。

3 基于离散元理论的显式弧长法

3.1 动力阻尼技术

当不考虑粘滞阻尼时，式(3)简化为：

此时分析过程简单且变量少，但由于没有了阻尼的抑制作用，系统会发生简谐振动，为此，引入动力阻尼技术[15]，即每时步计算后，由下式计算结构的动能：

式中，N为总颗粒数。

对于静力问题，在分析过程中，结构产生的动能大部分会转化为势能，其动能会减小，若此时的动能小于上一时刻计算的动能，则将所有颗粒的速度矢量设置为0 向量，然后进行下时步分析。

利用式(10)可计算出Δt时间步内各颗粒的位移增量：

在式(12)中，结构所受的外力Pt可由一个未知荷载参数λt+Δt与施加的静荷载P0的乘积表示，即：

3.2 总位移约束显式弧长法

在t+Δt时刻，每个颗粒的位移可表示为：

将式(13)代入式(14)，整理得：

式中：

为确定式(13)中荷载参数λt+Δt值，引入总位移弧长约束方程[5]：

式中，ln+1为指定的总弧长值。

将式(15)代入式(17)中，整理可得：

式中：

求解式(18)得荷载参数：

当式(20)中的根式大于0 时，方程有两个实根分别为λ1、λ2，与之对应的位移为dt+Δt,1、dt+Δt,2，分别求出此时两位移向量与上一时刻位移向量的“夹角”：λt+Δt的值由以下条件式确定[8]：

式中：Fj和P0,j分别为加载颗粒j在加载方向上所受内力和静荷载。

3.3 显式弧长法的具体计算流程

图4 给出了总位移约束弧长法的基本思想和收敛过程[15]。从图中可以看出，一个弧长步计算包含2 个计算过程：预测过程和校正过程[8]。

图4 总位移约束显式弧长法示意Fig.4 Explicit arc-length method for total displacement constraint

预测过程是一个力加载过程：首先确定每时步荷载增量detP；然后进行η 次离散元循环计算，并通过式(17)计算第η 次循环后的弧长ln+1。

离散元法其本质是动力分析，对于静力问题，可以采用阻尼耗能和缓慢施加外荷载方式逼近结构静力解，因此每时步荷载增量detP取值不宜过大，否则可能导致算法失效。若获得结构准静力解所需加载时间为Ttol(可取1 s～100 s)，则每时步荷载增量可取式(23)计算值或更小值。参数η 决定柱面弧长的校正频率，一般可取10～100，当detP取值较大时，结构响应可能发生较小波动，此时η 可取较小值，增加校正次数，以获得稳定解。

式中，P0为施加的静荷载。

校正过程：引入弧长约束方程式(17)，且在整个校正过程中弧长值ln+1保持不变。由式(18)～式(22)确定新的荷载系数 λ′，并在该荷载系数下进行离散元分析，当不平衡力R的范数小于容许值χ(其取值比detP小2～3 数量级)时，结束校正过程，然后进入下一弧长步计算；否则，再由弧长约束方程确定新的荷载系数λt+Δt，继续循环迭代，直至满足收敛要求。

图5 为基于离散元理论的显式弧长法的计算流程。

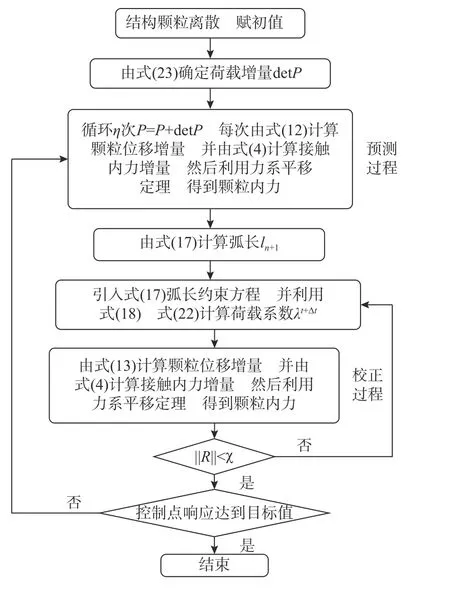
图5 基于离散元理论的显式弧长法计算流程Fig.5 Calculation flow of explicit arc-length method based on discrete element theory

4 算例分析

4.1 二杆平面桁架结构

图6 为一桁架结构，其顶端C点受竖向集中荷载P作用。该桁架的屈曲分析是经典的跳跃问题，集中外荷载P与顶点位移x的理论关系为[33]：

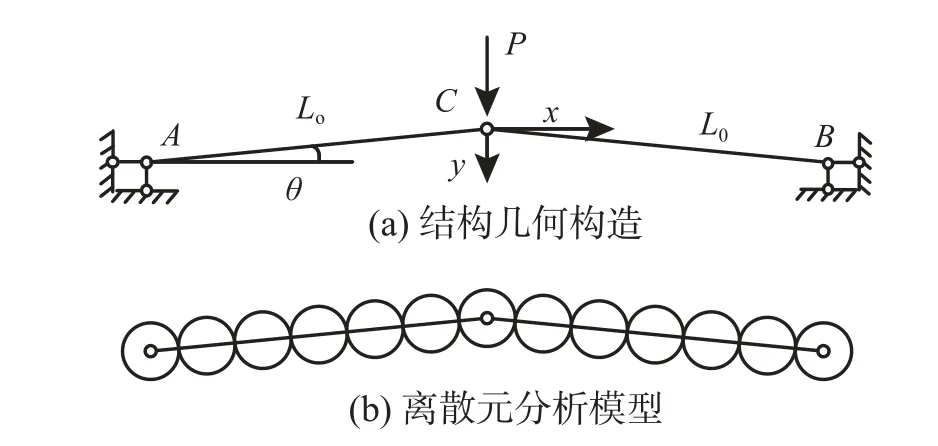
图6 二杆平面桁架结构及DEM 模型Fig.6 Two-bar truss structure and DEM analysis model

式中：弹性模量E=200 GPa；杆件横截面积A=10 mm2；惯性矩I=745.18 mm4；θ=6°；x=V/L0，V为顶点C的竖向位移，L0=100 mm。

ANSYS 分析时，对于桁架结构采用Link8 单元，单元划分采用一杆一单元；对于刚架结构采用Beam4 梁单元，不考虑杆件的剪切变形，单元划分采用一杆三单元形式，即将网壳结构每根杆件划分为3 个单元，并采用弧长法进行结构失稳全过程跟踪。后文算例亦按此方法进行ANSYS 有限元分析。建立DEM 分析模型时，将该结构离散为13 个相同的颗粒球单元，接触(单元)数量为12，计算时步取Δt=10-3s。弧长法分析参数为，加载点C处的y向静荷载P0=2500 N，每时步荷载增量detP=1 N，迭代次数η=10，循环最大容许值χ=1×10-2N。图7 为C点荷载-位移曲线，可以看出，本文方法计算结果与理论解及ANSYS 分析结果基本一致，曲线几乎完全吻合，说明本文给出的铰固单元本构模型合理性，同时也验证了本文基于离散元理论建立的显式弧长法的正确性。

图7 C 点荷载-y 方向位移曲线Fig.7 C point load-y direction displacement curve

在离散元显式弧长法中，参数detP的取值对算法收敛起决定作用，图8 为不同detP取值下C点的荷载-位移曲线，可以看出，在式(23)确定的估算值范围内，算法均可以得到正确结果。相比有限元分析软件中的弧长法，本文方法参数少、稳定性好，同时参数取值容易，无需使用者有足够经验，即可完成对结构的屈曲分析。但由于离散法中颗粒较多，分析步长Δt通常取值很小，其计算成本相对较高，且detP取值越小，计算时间越长，见表1。

表1 不同分析工况下计算时间Table 1 Calculation time under different cases

图8 不同分析工况下C 点荷载-y 方向位移曲线Fig.8 Load-y direction displacement curve of point C under different analysis cases

4.2 24 杆星型网穹结构

图9 为空间六角形星型穹顶结构，该结构已被用作桁架模型非线性分析的验证示例。星型穹顶在顶点中心节点1 处施加z向集中荷载P，构件截面均为正方形且尺寸相同，截面积A＝317 mm2，截面惯性Iy=Iz=8370 mm4，扭转惯性矩Ix=14 110 mm4，弹性模量E=3030 MPa，剪切模量G=1262 MPa，材料为线弹性，六个支座均为铰接。

图9 24 星型穹顶结构 /mmFig.9 24-bar star dome structure

该网穹结构共有13 个节点，24 根杆件，建立DEM 分析模型，节点球径取25 mm，对杆件剩余部分以接近节点球径为原则进行均等离散，如图10 所示，结构最终被离散为121 个球元，共形成132 个接触单元，计算时步取Δt=10-3s。弧长法分析参数为，节点1 处的静荷载P0=900 N，detP=0.5 N，η=10，χ=1×10-3N。

图10 24 星型穹顶结构离散元模型Fig.10 DEM analysis model of 24-star dome structure

图11、图12 分别为记录点的荷载-位移曲线，可以看出，本文方法计算结果与文献[34]及ANSYS 分析结果基本相同，曲线几乎完全吻合，说明本文给出的铰固单元本构模型和基于离散元理论建立的显式弧长法的正确性，并能够有效跟踪结构弹性屈曲全过程。

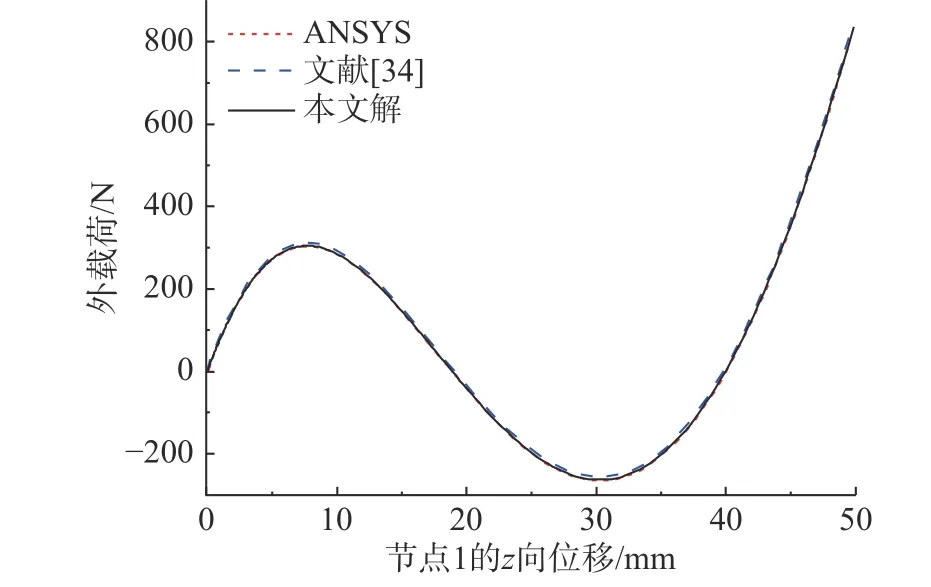
图11 节点1 的荷载-位移曲线Fig.11 Load-displacement curve of node 1

图12 节点2 荷载-位移曲线Fig.12 Load-displacement curve of node 2

图13 为不同detP取值下节点1 的荷载-位移曲线，可以看出，曲线几乎完全重合，说明采用式(23)计算的detP估算值，算法是稳定的。表2为不同分析工况下的计算时间，detP取值越小，耗时越长，此时可增大η 取值，以降低柱面弧长校正频率，减少分析时间。

图13 不同工况下节点1 荷载-位移曲线Fig.13 Load- displacement curve of node 1 under different analysis cases

4.3 K6-4 单层穹顶网壳结构

如图14 所示的K6 型单层穹顶网壳结构，跨度L为30 m，矢高为2 m，采用ϕ180×5 钢管，材料弹性模量E=210 GPa，剪切模量G=85 GPa，网壳仅在节点1 作用竖向集中荷载P，支座采用周边铰接。建立离散元模型时将各杆件划分为7 个球颗粒，结构共划分为841 个球颗粒，如图15 所示，接触(单元)数量为936，计算时步取Δt=10-4s。弧长法分析参数为，节点1 处静荷载P0=1000 kN，detP=0.1 kN，η=10，χ=1×10-3kN。

图14 K6 型单层穹顶网壳结构 /mFig.14 K6 single dome structure

图15 K6 型单层穹顶网壳结构离散元分析模型Fig.15 DEM analysis of K6 single dome structure

图16 为节点1～节点3 的荷载-位移曲线，可以发现，结构在第一次屈曲前，本文方法得到的曲线与文献[27]及ANSYS 分析方法得到曲线基本吻合。在第一次屈曲后，本文方法和文献[27]基于离散元理论采用位移控制法得到的曲线整体趋势相近，仅在数值上存在较小的差异；但与ANSYS 分析结果相比，曲线无论在走势和数值上都存在较大差异，这可能是因为离散元法是一种非连续介质力学方法，有限元法是连续介质力学方法，两种分析方法的理论基础和算法模式不同，计算结果会存在一定的差异，当结构发生屈曲后，结构处于不稳定状态，这种差异性可能更为突显。

图16 节点1～节点3 的荷载-z 方向位移曲线Fig.16 Load-direction displacement curves of nodes from 1 to 3

图17 为不同detP取值下节点1 的荷载-位移曲线，可以看出，三种分析工况得到的曲线基本吻合，说明在式(23)确定的detP估算值下，算法是稳定的。detP较小的取值保证了算法的稳定性，但需要更多的计算时间，见表3。

图17 不同工况下节点1 荷载-z 向位移曲线Fig.17 Load-z direction displacement curve of node 1 under different analysis cases

5 结论

本文基于杆系离散元理论，提出了一种显式弧长法，用于追踪结构屈曲全过程曲线。对典型算例和单层网壳结构的弹性失稳问题进行了研究，得到主要结论如下：

(1) 建立了新型接触单元—铰固接触单元的本构模型，分别采用离散元法和结构力学方法对铰固接触单元在已知端部位移工况下进行受力分析，并通过端部内力相等建立方程，推导了接触刚度系数，丰富了离散元法的接触单元类型，扩大了其应用范围。

(2) 在离散元显式弧长法中，每时步荷载增量detP的取值对算法收敛至关重要，采用本文方法确定的detP估算值，可保证算法稳定性，其取值越小，算法越稳定；参数η 控制柱面弧长约束的校正频率，当detP较小时，其取值可稍大些。相比传统有限元弧长法，该算法参数少、稳定性好，且参数取值容易，对分析者自身能力与经验要求低，但计算成本相对较高。

(3) 在求解颗粒运动方程时，采用动力阻尼技术获取结构的准静态解，因无粘滞阻尼项，大大简化了计算过程，并有效地与总位移约束弧长法衔接。同时，本文方法无需组集单元刚度矩阵和迭代求解方程组，就可以越过结构屈曲的临界点，与传统有限元方法相比更具优越性，为结构失稳分析提供了新的算法工具。