双足被动行走模型局部稳定性分析
胡运富,赵 杰,朱延河,臧希喆
(哈尔滨工业大学机器人研究所,哈尔滨150001,huyunfu134@yahoo.com.cn)
相对于传统机器人而言,被动步行机器人以其结构和控制简单,步态自然,节能和在非结构化环境中具有更好的移动能力等特点引起广大学者的极大关注[1].加拿大学者McGeer发现[2-3]:完全不用驱动和控制的机器人也能实现稳定的下坡运动,并提出“被动动力步行”概念.Garcia[4],Collins[5]等对机器人行走的参数匹配问题进行了研究.Grizzle从理论上证明了被动双足机器人前向运动存在复杂零动态子系统,给出稳定极限环存在的条件[6],并通过Rabbit实现了稳定动态步行[7].当前,稳定性问题严重制约了被动机器人的发展,影响被动机器人模型稳定行走的因素很多,同时被动机器人本体的设计必须要建立在其能稳定行走的基础上.
本文分析了机械参数和斜面坡度对被动行走模型局部稳定性的影响,为后续被动机器人全局稳定性分析以及机器人本体机械参数设计提供指导和理论依据.
1 被动行走模型
所讨论的被动行走机器人模型是两刚性匀质的直腿圆弧足模型,如图1所示.两腿通过髋关节相连,髋关节为无质量、无摩擦、无阻尼的被动铰链.这种模型明显优化于传统的点足模型,更接近于真实的机器人样机.每条腿质量为m,其相对质心的转动惯量为J,腿长均为l,质心距离髋关节的距离为c,圆弧足的足半径为r,斜面坡度为β.
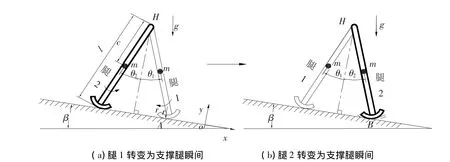
图1 被动行走模型
当给定初始条件,在重力和自身的惯性作用下,该被动动力模型可沿小坡度的刚性平坦斜面稳定地向下行走.其每一步的运动过程可分为如下两部分.
1)当摆动腿离开地面时,支撑腿绕支撑足做倒立摆运动(支撑足与地面是纯滚动),而摆动腿则绕髋关节做单摆运动.此过程为连续运动阶段.该过程中只有重力做功,故其总的机械能是守恒的.
为使所建立的动力学方程适用性更广,将方程无量纲化,令KJ=J/ml2,Kr=r/l,KC=c/l,且将时间无量纲化为由拉格朗日方程推导该阶段的动力学方程,可得

其中:
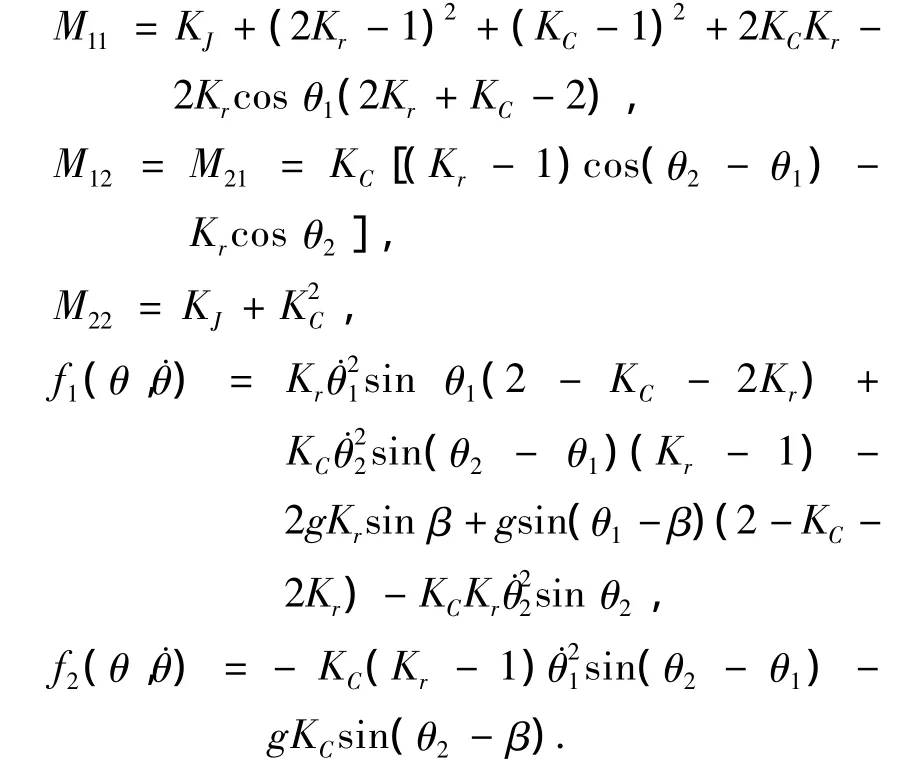
2)当摆动腿与地面碰撞后,摆动腿和支撑腿角色互换,假设碰撞是瞬时的,完全非弹性(摆动足与地面无滑动),故在碰撞前后,两腿角速度发生突变,而两腿角度不变,系统满足角动量守恒.描述碰撞过程:设碰撞瞬间前后分别用上角标“-”和“+”表示,系统角动量用L表示.
对于碰撞点B和髋关节H角动量守恒:
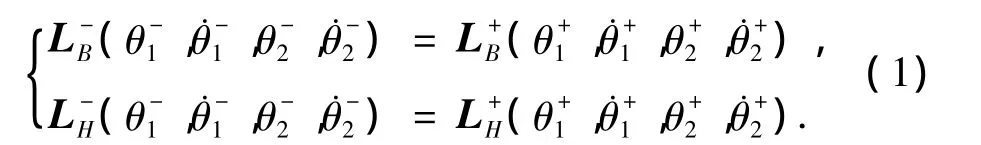
由前述分析知:
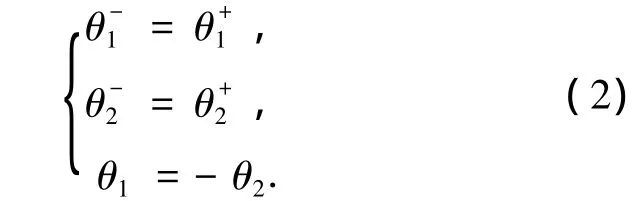
该无膝被动模型的摆动方程和碰撞方程构成了一个完整步态周期的动力学模型,是后续的仿真和稳定性分析的基础.
2 稳定不动点的求解
如图1所示,被动机器人的运动过程可由状态变量φ(t)=(θ1,θ2,˙θ1,˙θ2)来描述,每个状态变量对应空间中的一个点,由这些点构成的空间称为“相空间”.令机器人双足着地的状态是某步的起始状态或终点状态,通过研究双足着地的状态,可判断机器人运动的周期稳定性.双足同时着地时由图1知θ1=-θ2,故其状态可由状态变量φ(t)=(θ1,˙θ1,˙θ2)来表示.
设不动点为被动机器人稳定周期运动时,腿1刚与地面相碰后,转为支撑腿的瞬间(此时双腿同时着地)所对应的状态在相空间中的点用φfP(t)=(θ1,˙θ1,˙θ2)表示.不动点的存在是被动机器人能稳定行走的必要条件.由于为非线性系统,机器人每走一步即为一次庞加莱映射S(S是包括碰撞在内的一次完整的动态步行的表达式,它反映相邻两步之间的关系),即φn+1=S(φn),显然对于稳定的周期运动有φfP=S(φfP).当所给的初始条件非常接近于不动点时,则模型可收敛到稳定的运动.影响不动点存在的因素为该被动模型的机械结构参数和斜面的坡度.
首先考虑如何求被动模型稳定不动点,所有的初始条件可以写为不动点和偏差的和:
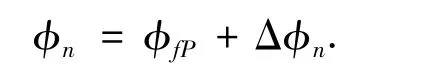
对于偏离不动点的小的偏差Δφn,可用线性化的方法来估计相空间:
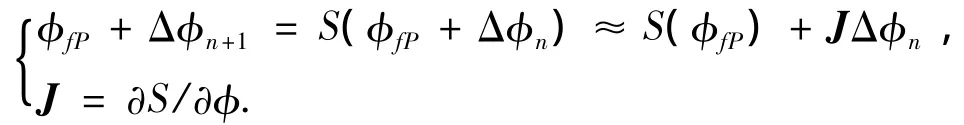
方程简化为Δφn+1=JΔφn,J为雅克比矩阵,其特征值的模是进行局部稳定性分析的关键.如果其模小于1,则说明结果将收敛于稳定不动点.当所给的初值接近于不动点的一定范围内,通过牛顿-拉普森迭代函数可快速求得不动点.过程如下:
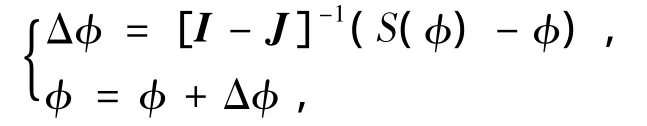
重复直到|Δφ|<ε.
3 局部稳定性分析
对模型局部稳定性的分析就是对模型不动点的存在与否,机器人在所给的初始条件下收敛到不动点的快慢程度以及各参数对不动点状态分量变化的影响进行分析.机器人运动的不动点是否存在与所给初始条件无关,只和该模型的机械参数和斜面的坡度有关.现举例分析,如表1.

表1 每条腿的参数
在此基础上逐一分析各参数对机器人局部稳定性的影响:方法是在保证其他参数不变的情况下,只改变某一个参数的值,判断雅克比矩阵的特征值的模的变化,若模大于或等于1,则模型无稳定的不动点;若模小于1则有稳定的不动点,模越小则收敛到不动点的速度就越快(即模型在所给初始条件下收敛到稳定运动状态的速度就越快).
如图2为模型在Matlab仿真下的运动动画,所有分析都是基于模型可以行走的条件下进行,这样获得的结果更为可靠,对被动机器人的设计具有很好的指导意义.

图2 仿真模型运动动画
从图3(a)中可看出当腿质量过小时(约小于0.3 kg),会出现特征值的模大于1,被动模型会出现无稳定的不动点,即不具有稳定周期运动的必要条件;此后在m∈[0.3 kg,30 kg]之间时,特征值的模小于1,说明该模型具有稳定的不动点,但随着腿质量的增大,特征值的模也随之增大,这意味着被动模型收敛到稳定周期运动状态的速度逐渐变慢,同时可看出m∈[0.3 kg,5 kg]之间时特征值的模对质量的变化非常敏感(这为设计机器人提供依据:尽量取较小质量的腿,以便于通过微调腿的质量来改善机器人的局部稳定性);由特征值的模随质量增加而增大的趋势可看出,当质量过大时会出现特征值的模大于1,即稳定不动点会消失.
图3(b)中可看出:稳定不动点在相空间的位置随着腿质量的增大,沿曲线按箭头所指方向运动.
图3(c)为不动点的状态随质量的变化曲线.随着腿质量的增加,θ1单调减小,而˙θ1,˙θ2的绝对值呈单调增加趋势,在m∈[0.3 kg,5 kg]时,这种变化比较明显.可见,当被动机器人具有稳定不动点时,腿质量对其模型最终的稳定运动状态也有很大影响.
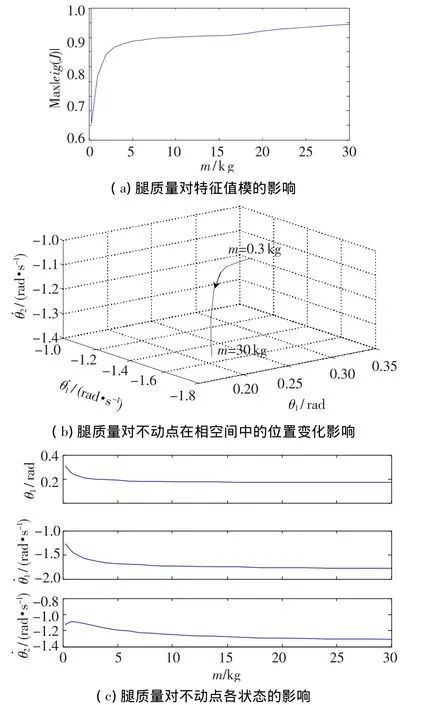
图3 腿质量对局部稳定性的影响
从图4(a)中可看出,当Kc过小(约小于0.03)即质心位置过高时,特征值的模大于1,机器人不具有稳定状态;当Kc∈[0.030 4,0.624 0]时,特征值的模小于1,机器人有稳定的不动点,但随着Kc的增大,特征值的模也在增大,被动机器人收敛到稳定运动状态的速度越慢,且在Kc∈[0.030 4,0.200 0]和Kc>0.600 0时特征值的模对质心位置的变化非常敏感(这为设计机器人提供依据:尽量取Kc∈[0.030 4,0.200 0]腿,既有较快的收敛速度也便于通过微调腿的质心位置来改善机器人的局部稳定性);当Kc>0.624 0后机器人不具有稳定的运动状态;可见质心位置过低(Kc<0.03)和过高(Kc>0.6240)都不利于被动机器人的稳定运动.
图4(b)中可看出:稳定不动点在相空间位置随Kc的增大,沿曲线按箭头所指方向移动.
图4(c)为不动点的状态随质心位置的变化曲线.随着Kc的增加,θ1单调减小,而 ˙θ1,˙θ2的绝对值呈单调增加趋势,可见当被动机器人具有稳定不动点时,质心位置对其最终的稳定运动状态也有很大影响.
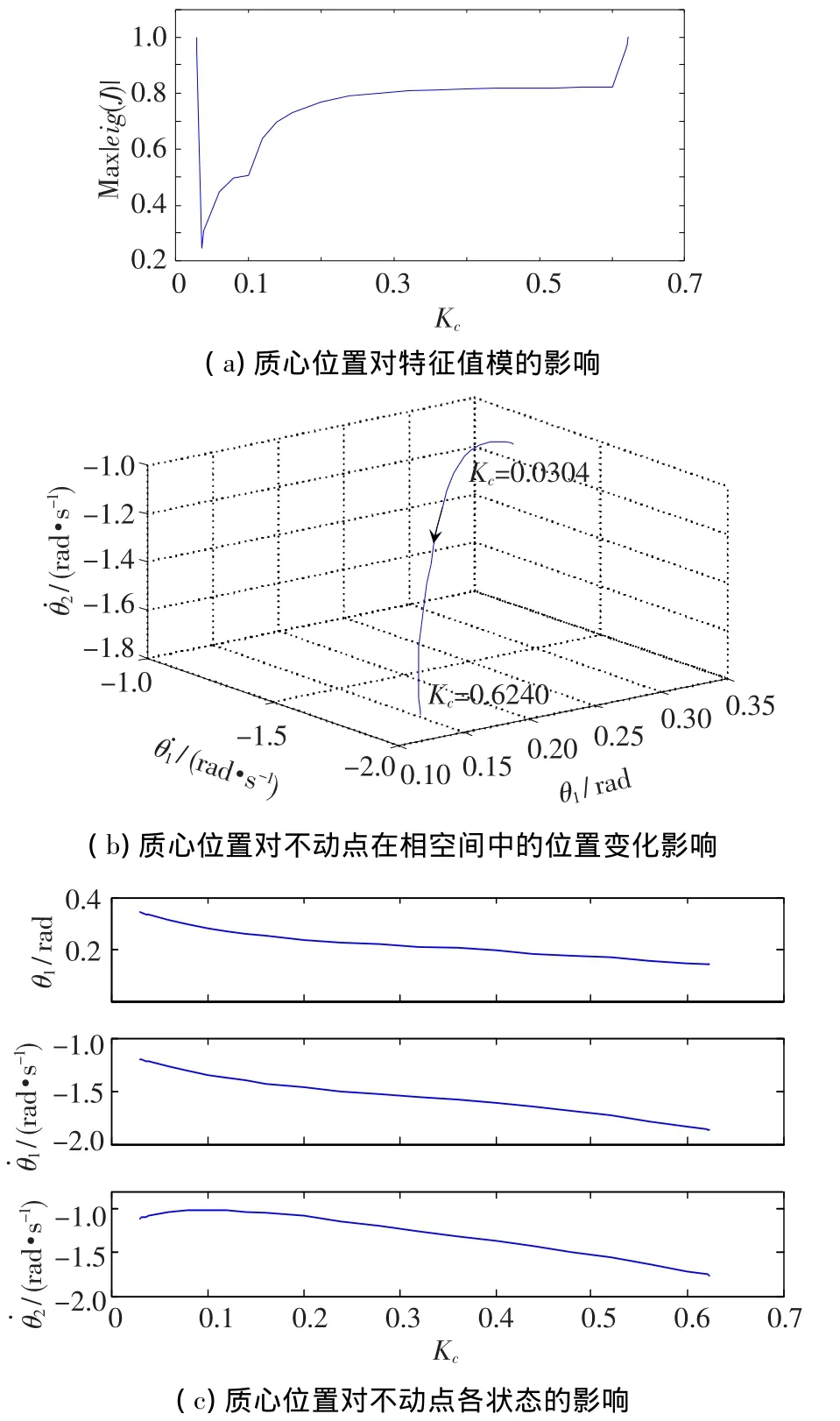
图4 质心位置对局部稳定性的影响
从图5(a)可看出,雅克比特征值的模并不随足半径的增大而单调变化,但当Kr<0.84时,特征值的模都小于1,即模型存在稳定的不动点;当Kr∈[0,0.16]之间时特征值的模单调减小;当Kr∈[0.16,0.84]之间时特征值的模单调增大,即模型收敛到稳定状态的速度减慢.当足半径在Kr=0.16附近时,特征值变化敏感(这为设计机器人提供依据:尽量取Kr=0.16附近的足半径,既有较快的收敛速度也便于通过微调足半径来改善机器人的局部稳定性).
图5(b)中可看出稳定不动点在相空间位置,随着Kr的增大,沿曲线按箭头所指方向移动.
图5(c)为不动点的状态随质心位置的变化曲线.随着Kr的增加,θ1呈增大趋势,˙θ1,˙θ2的绝对值也呈增大趋势,可见当被动机器人具有稳定不动点时,足半径对其最终的稳定运动状态也有很大影响.
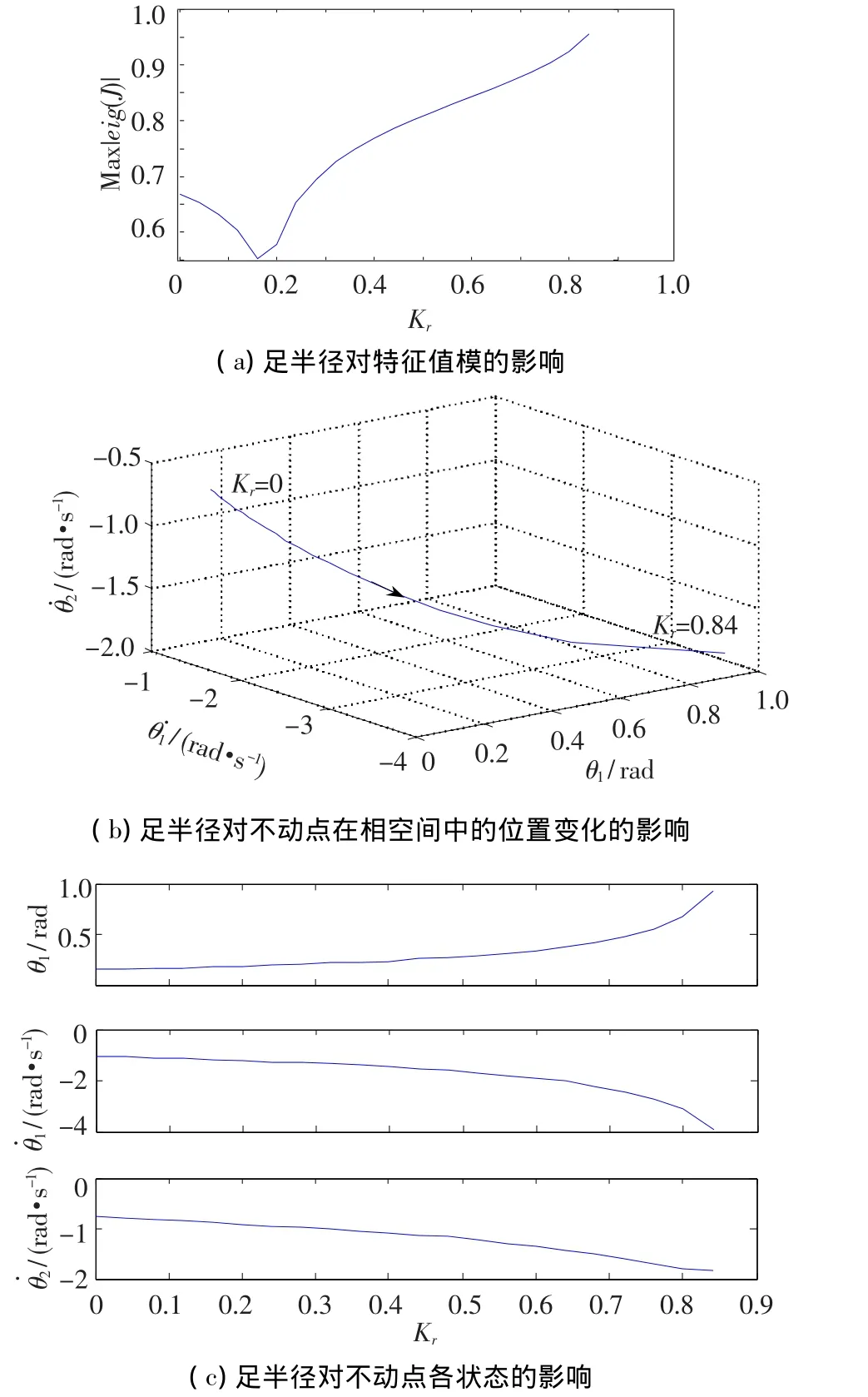
图5 足半径对局部稳定性的影响
从图6(a)中可看出,特征值的模并不随转动惯量的增大而单调变化,当KJ∈[0,0.154]时,特征值的模小于1,被动模型具有稳定的不动点,特征值的模在KJ=0.128时,特征值的模具有最小值,即模型具有最快的收敛速度(这为设计机器人提供依据:尽量取KJ=0.128附近的转动惯量,既有较快的收敛速度也便于通过微调转动惯量来改善机器人的局部稳定性);当KJ>0.154时,特征值的模大于1,可见此时系统不具有稳定行走的必要条件.
图6(b)可看出:不动点在相空间位置随着KJ的增大,沿曲线按箭头所指方向移动.
图6(c)为不动点的状态随腿的转动惯量的变化曲线.随着转动惯量的增加,θ1,˙θ1,˙θ2都呈单调变化趋势:θ1增大,而˙θ1,˙θ2的绝对值减小.可见当被动机器人具有稳定不动点时,转动惯量对其最终的稳定运动状态也有很大影响.
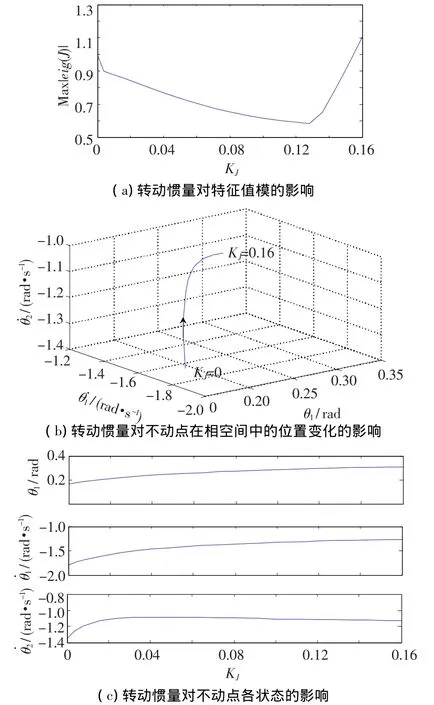
图6 转动惯量对局部稳定性的影响
从图7(a)中可看出,特征值的模并不随坡度的增大而单调变化,而是先减小(β∈[0,0.021 rad]),后增大(β∈[0.021 rad,0.038 rad]),再减小(β∈[0.038 rad,0.1 rad]),最后再增大(β>0.1 rad).
图7(b)可看出:不动点在相空间位置随着β的增大,沿曲线按箭头所指方向移动.
图7(c)为不动点的状态随坡度变化的曲线.随着坡度的增加,θ1增大,而˙θ1的绝对值减小,˙θ2的方向由负变为正.可见当被动机器人具有稳定不动点时,坡度对其最终的稳定运动状态也有很大影响.

图7 斜面坡度对局部稳定性的影响
4 结论
1)给出了如何求被动机器人稳定不动点的方法,同时详细分析了模型的各机械参数和斜面坡度对机器人局部稳定性的影响.
2)较小的腿质量(m∈[0.3 kg,30 kg],考虑到收敛的快速性和被动机器人的刚度和强度,可取 m=1 kg),较高的质心位置 (Kc∈[0.0304 0,0.624 0],同时考虑到被动机器人稳定行走鲁棒性,取 Kc=0.2),合适的足半径(Kr=0.16),较大的转动惯量(KJ=0.128)以及合适的斜面坡度(β∈[0.02 rad,0.10 rad],同时考虑到被动机器人稳定行走鲁棒性可取β= 0.02 rad)有利于提高被动机器人的局部稳定性.
3)被动机器人的局部稳定性分析和后续全局稳定性分析将为被动机器人本体样机的设计提供指导和理论依据.
[1]HUANG Q,YOKOI K,KAJITA S,et al.Planning walking pattems for a biped robot[J].IEEE Transactions on Robotics and Automation,2001,17(3):280-289.
[2]MCGEER T.Passive dynamic walking[J].International Journal of Robotics Research,1990,9(2):62-82.
[3]MCGEER T.Passive dynamic biped catalogue[C]//In Chatila R and Hirzinger,editors,Proc,Experiment Robotics II:The 2nd International Symposium.Berlin: Springer-Verlag,1992:465-490.
[4]GARCIA M,CHATTERJEE A,RUINA A,et al.The Simplest Walking Model:Stability,Compiexity,and Scaling[J].ASME Journal of Biomechanic Engineering,1998,120(2):281-288.
[5]COLLINS S H,WISSE M,RUINA A.A 3-d passive dynamic walking robot with two legs and knees[J].International Journal of Robotics Research,2001,20 (7):607-615.
[6]GRIZZLE J W,GABRIEL A,PLESTAN F.Asymptotically Stable Walking for Biped Robots:Analysis via Systems with Impulse Effects[J].IEEE Transactions on Automatic Control(S0018-9286),2001,46(1):51-64.
[7]CHEVALLEREAU C,ABBA G,AOUSTIN Y,et al.RABBIT:A Test bed for Advanced Control Theory[J].IEEE Control Systems Magazine CSM-02-038 Revision(S0272-1708),2003,08(6):57-79.

