一个新型自适应预条件的总体CGS算法

赵 静

(安徽科技学院 数学系，安徽 凤阳 233100)

一个新型自适应预条件的总体CGS算法

赵 静

(安徽科技学院 数学系，安徽 凤阳 233100)

总体 CGS算法(Gl-CGS)是求解具有多个右端项大型稀疏非对称线性方程组的一个有效矩阵 Krylov子空间方法.然而，在一些实际问题中Gl-CGS算法常常收敛得很慢甚至停滞.针对此问题，将总体CGS算法嵌入总体GMRES迭代过程，构造了一个新型自适应预条件子.最后，数值试验表明此预条件子的有效性.

矩阵Krylov子空间方法；多右端项；总体CGS算法；总体GMRES算法

0 引言

在频域电磁波散射计算等问题中，人们常常需要计算如下具有多个右端项大型稀疏非对称线性方程组的解

其中A为N×N阶实矩阵，X=[x(1),x(2),…,x(s)],B=[b(1),b(2),… ,b(s)]为N×s阵且s＜＜N.

近年来求解方程组(1)的一些块Krylov子空间方法得到了迅猛发展.基于块Arnoldi过程，Vital[1]提出了块GMRES (Bl-GMRES)方法，之后很多学者[2-5]对其进行了深入研究和改进.基于块 Lanczos过程，产生了一些经典有效的块Krylov子空间方法，如块CG方法(Bl-CG)[6]295、块BiCG方法(Bl-BiCG)[6]296、块BiCGSTAB方法(Bl-BiCGSTAB)[7]、新型块Lanczos型方法[8]及块QMR方法(Bl-QMR)[9].当方程组(1)的右端项不能同时获知时，种子投影法是十分有效的；详见文献[2,10-11].

最近产生第三种求解方程组(1)的热门方法即总体Krylov子空间方法，其主要思想是在矩阵Krylov子空间上采用正交投影或斜投影技术.Jbilou等[12]49、Heyouni等[14]317分别提出了求解方程组(1)的总体 GMRES方法(Gl-GMRES)[12]55，总体BiCG类方法[13]119，总体CMRH方法(Gl-CMRH)[14]323和加权总体CMRH方法[15].林依勤[16]提出了隐式再开始的Gl-GMRES方法.当系数阵为对角阵时，Bellalij等人[17]分析了Gl-GMRES方法的收敛性.基于总体Lanczos过程，一些学者提出了一类总体Lanczos型方法；详见文献[18-19].

为避免矩阵转置乘积，张建华和戴华[19]390给出了总体 CGS算法(Gl-CGS)，数值实验表明此方法的收敛速度为Gl-BiCG算法的将近一倍.然而在某些复杂的实际问题中，Gl-CGS算法的残量范数常呈现不规则行为或收敛速度很慢.借鉴文献[20-21]的思想，本文构造一个新型自适应预条件子.该预条件子实际是一个多项式预条件子，它由Gl-CGS算法嵌入总体GMRES过程隐式构造而成.新方法能减少迭代步数，伴随迭代步数的减少，存贮量会降低，运算量也会下降.

1 自适应预处理的Gl-CGS算法

数值实验表明Gl-CGS 算法收敛速度比Gl-BiCG算法快，然而在一些实际问题中，Gl-CGS 算法收敛得很慢甚至停滞.因此，如何选择恰当的预条件子成为Gl-CGS 算法高效求解的关键.下面给出预条件子的构造过程.借鉴文献[23]的思想，把Gl-CGS 算法应用到预处理方程组

算法1一般预处理的Gl-CGS 算法

选择初始估计矩阵X0，计算R0=B-AX0，选择矩阵

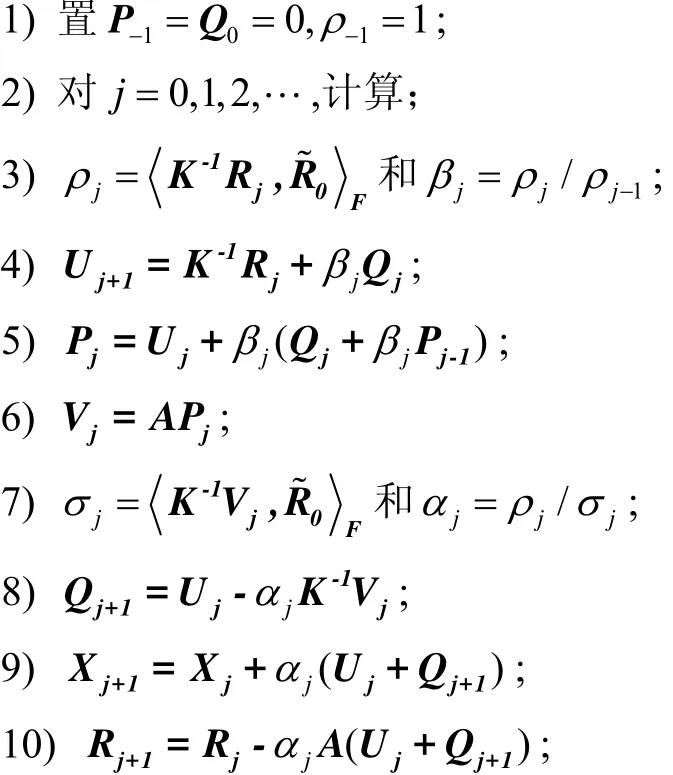
11) 结束.

算法1的每一步迭代都需要计算K−1Rj和K−1Vj.一个好的预条件子需满足如下性质：

1) 预条件后的方程应该容易求解；

2) 预条件子应该较容易构造且应用预条件子的代价不能太高.

下面给出一个新型预条件子K的隐式构造过程.即对∀F∈RN×s，当计算K-1 F时，都转化为求解方程组AW=F,然后使用Gl-GMRES(m)方法迭代k步，得Wk来逼近K−1F，其中k常取2或3，m的值由实际问题而定，W0取为零矩阵.

算法2 新型自适应预处理的Gl-CGS算法 (PGl-CGS)

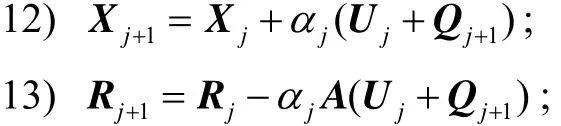
当s= 1时，PGl-CGS算法转化为曹海燕等人提出的CGS/GMRES(m)算法[21]147.该预条件也可应用到GliCG和Gl-BiCGSTAB等算法中，我们将在另文中研究此问题.

2 数值例子

本节通过一个数值例子说明PGl-CGS算法的有效性.数值实验在Matlab环境下运行，初始估计值取为零矩阵.右端项B=rand(N,s)，其中rand产生一个系数分布在区间[0,1]上的一个N×s随机矩阵.实验终止条件为.Its,Times和TRR分别表示迭代步数，计算时间和相对残量F范数的常用对数值.

在本例中，比较PGl-CGS算法与Gl-CGS，WGl-GMRES[15]149和Gl-BiCGSTAB[13]131算法求解方程组(1)的有效性.实验所用矩阵分别来于流体动力学(CDDE2,CDDE4)，石油存贮模拟(ORSREG1)，偏微分方程(PDE900)和反应扩散 brusselator模型(RDB200L).置R~0=R0,s=5,m=20,k=3.所有算法迭代步数不超过200.当用Gl-GMRES(m)算法构造预条件子时，初始矩阵都取为零矩阵.

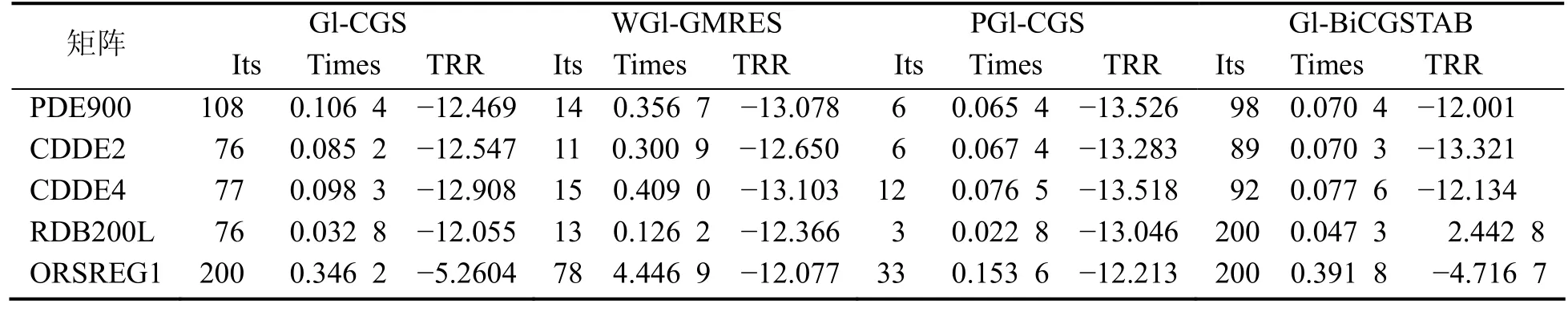
表1 矩阵及Gl-CGS, WGl-GMRES, PGl-CGS, Gl-BiCGSTAB算法的数值结果

由表 1可以看出，同其他 3种算法比较，PGl-CGS算法收敛速度快且求解精度好.对矩阵 RDB200L而言，Gl-BiCGSTAB算法在200步内不收敛；对矩阵ORSREG1而言，Gl-CGS和Gl-BiCGSTAB算法的求解精度分别仅仅达到−5.260 4和−4.716 7.在图 1中，横坐标表示迭代次数，纵坐标表示残量 F-范数的常用对数.从图 1可以看出，Gl-CGS算法的残量震荡激烈呈现不规则收敛行为而 PGl-CGS算法的残量收敛比较光滑.PGl-CGS算法的迭代步数、计算时间和存贮量都比WGl-GMRES少.

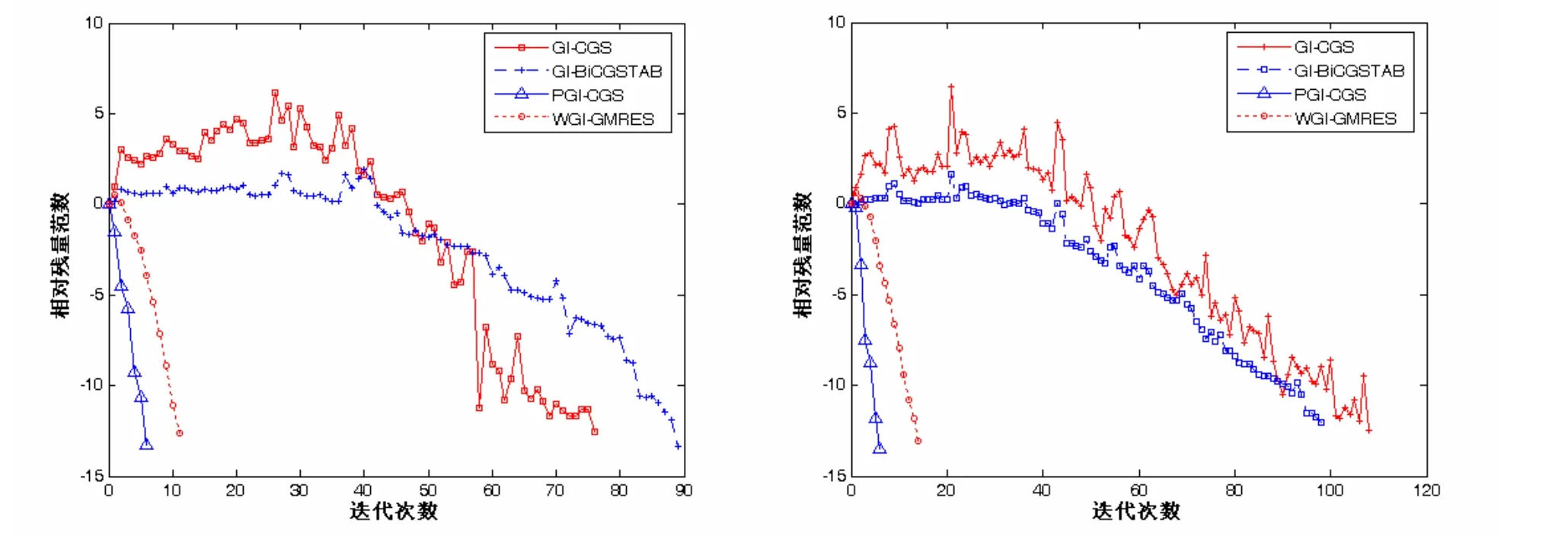
图1 矩阵CDDE2(左)和矩阵PDE900(右)的收敛行为

[1] VITAL B. Etude de quelques methodes de resolution de problemes linearies de grade taide sur multiprocesseur [D]. Universite de Rennes, Rennes, France, 1990.

[2] SIMONCINI V, GALLOPOULOS E. An iterative method for nonsymmetric systems with multiple right-hand sides[J]. SIAM J. Sci. Comput, 1995, 16:917-933.

[3] SIMONCINI V, GALLOPOULOS E. Convergence properties of block GMRES and matrix polynomials[J]. Linear Algebra Appl, 1996, 247:97-119.

[4] GU G D, CAO Z H. A block GMRES method augmented with eigenvectors[J]. Appl. Math. Comput, 2001, 121:271-289.

[5] MORGAN R B. Restarted block-GMRES with deflation of eignvalues[J]. Appl. Numer. Math, 2005, 54:222-236.

[6] O’LEARY D P. The block conjugate gradient algorithm and related methods[J]. Linear Algebra Appl, 1980, 29:293-322.

[7] GUENNOUNI A E, JBILOU K, SADOK H. A block version of BICGSTAB for linear systems with multiple right-hand sides[J]. Elec. Trans. Numer. Anal, 2003, 16:129-142.

[8] GUENNOUNI A E, JBILOU K, SADOK H. The block Lanczos method for linear systems with multiple right-hand sides[J]. Appl. Numer. Math, 2004, 51:243-256.

[9] FREUND R, MALHOTRA M. A block QMR algorithm for non-Hermitian linear systems with multiple right-hand sides[J]. Linear Algebra Appl, 1997, 254:119-157.

[10] CHAN T, WANG W. Analysis of projection methods for solving linear systems with multiple right-hand sides[J]. SIAM J. Sci. Comput, 1997, 18:1689-1721.

[11] SAAD Y. On the Lanczos method for solving symmetric linear systems with several right-hand sides[J]. Math. Comp, 1987, 48:651-662.

[12] JBILOU K, MESSAOUDI A, SADOK H. Global FOM and GMRES algorithms for matrix equation[J]. Appl. Numer. Math, 1999, 31:49-63.

[13] JBILOU K, SADOK H, TINZEFTE A. Oblique projection methods for linear systems with multiple right-hand sides[J]. Elec. Trans. Numer. Anal, 2005, 20:119-138.

[14] HEYOUNI M. The global Hessenberg and CMRH methods for linear systems with multiple right-hand sides[J]. Numer. Algorithms, 2001, 26:317-332.

[15] HEYOUNI M, ESSAI A. Matrix Krylov subspace methods for linear systems with multiple right-hand sides[J]. Numer. Algorithms, 2005, 40:137-156.

[16] LIN Y Q. Implicitly restarted global FOM and GMRES for nonsymmetric matrix equations and Sylvester equations[J]. Appl. Math. Comput, 2005, 167:1004-1025.

[17] BELLALIJ M, JBILOU K, SADOK H. New convergence results on the global GMRES method for diagonalizable matrices[J]. J. Comput. Appl. Math, 2008, 219:350-358.

[18] SALKUYEH D K. CG-type algorithms to solve symmetric matrix equations[J]. Appl. Math. Comput, 2006, 172:985-999.

[19] 张建华,戴华.求解具有多个右端项线性方程组的总体CGS算法[J]. 高等学校计算数学学报, 2008, 30:390-399.

[20] SAAD Y. A flexible inner-outer preconditioned GMRES algorithm[J]. SIAM J. Sci. Stat. Comput, 1993, 14:461-469.

[21] CAO H Y, LI X W. CGS/GMRES(k): An adaptive preconditioned CGS algorithm for nonsymmetric linear systems[J]. Numer. Math. J. Chinese Univ. (English Ser.), 1998, 7:145-158.

[22] SONNEVELD P. CGS: a fast Lanczos-type solver for nonsymmetric linear systems[J]. SIAM J. Sci. Statist. Comput,1989, 10:36-52.

[23] VAN DER VORST H A. “BiCGSTAB: A fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems,”[J]. SIAM J. Sci. Statist. Comput, 1992,13:631-644.

A New Adaptive Preconditioned Global CGS Algorithm

ZHAO Jing
(Department of mathematics, Anhui Science and Technology University, Fengyang, Anhui 233100, China)

Global CGS algorithm (Gl-CGS) is popular matrix Krylov subspace method for large, sparse and nonsymmetric linear systems with multiple right-hand sides. However, the Gl-CGS may suffer from slow convergence or be stationary in some applications. In order to remedy this, we present a new adaptive preconditioner, which is constructed in the iteration. step of Gl-CGS, by several steps of global GMRES (m). Finally, numerical experiments show the effectiveness of the new preconditioner.

matrix Krylov subspace; multiple right-hand sides; Gl-CGS; Gl-GMRES

O241.6

A

1673-2065(2011)04-0022-04

2011-02-11

安徽省教育厅自然科学一般项目(KJ2009B122Z)

赵 静(1982-),女,山东泰安人,安徽科技学院数学系教师,理学硕士.

(责任编校：李建明英文校对：李玉玲)