不可微非线性方程的修正牛顿迭代法的收敛性分析*

金皓苹， 徐秀斌

(浙江师范大学数理与信息工程学院，浙江金华 321004)

0 引言

令F是Banach空间X到Y的非线性算子，考虑如下一般的非线性方程：

求解非线性方程(1)的近似解是一个重要的问题，因为大量的不同类型的实际问题都可归结为对非线性方程的求解．例如，微分方程、边界值问题、积分方程等．目前，在F是Fréchet可导的条件下，牛顿法是求解非线性方程(1)的最有效方法之一，其迭代式为(初始点x0给定)

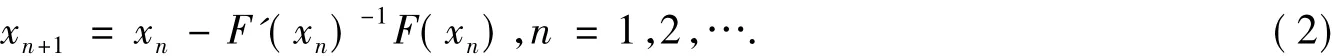
关于牛顿迭代法收敛性的研究目前已有许多，如文献［1-3］等．然而，当F不可导时，牛顿迭代法就不能再用来解非线性方程．对于F不可导情形的修正牛顿迭代的研究，主要归结为当F'(x)不存在时用什么来代替的问题．诸多文献考虑将F分解为可导部分H和不可导部分G，即

如文献［4-5］利用

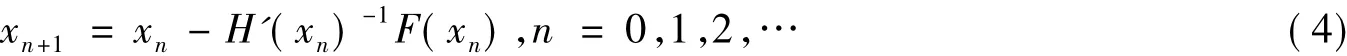
对方程(1)进行求解．

另外，文献［6-7］采用弦割法，用差商代替F'，利用

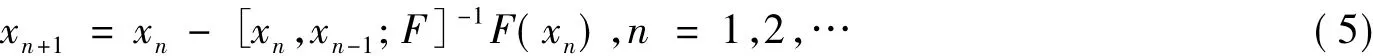
迭代对方程(1)进行近似求解，其中初始点x0，x-1给定．因为对G的限制，式(4)一般只能保持线性收

文献［8］将以上2种迭代方法结合起来，构造了新的迭代式

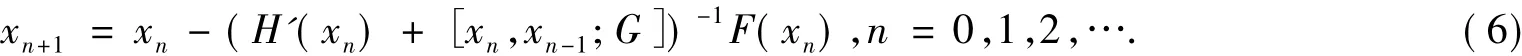
最近，文献［9］又利用差商［yn，xn;G］代替［xn-1，xn;G］，其中 yn=λxn+(1- λ)xn-1，λ∈［0，1］，并提出了修正的牛顿变形公式

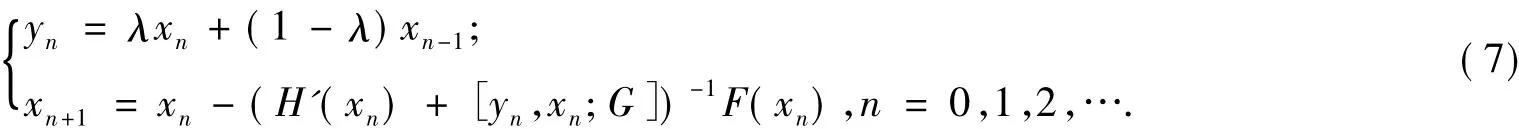
式(7)中，x-1，x0∈D已知．此迭代推广了迭代法(6)．文献［9］利用ω条件证明了其半局部收敛性并给出收敛定理．本文主要目的是引入L-平均Lipschitz条件，并使用优序列的方法分析式(7)的收敛性．下面总设X，Y为Banach空间，且F=G+H，其中H和G如式(3)定义，H为一阶Fréchet可导，G为连续但不可导函数．

1 引理

首先给出几个重要的引理，然后在这些引理的基础上证明修正牛顿迭代法式(7)的半局部收敛性、误差估界及解的唯一性．

引理1 设优函数

式(8)中，L(u)和l(u)为非负非减可积的连续函数．记

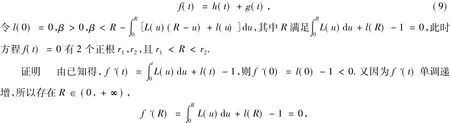
而

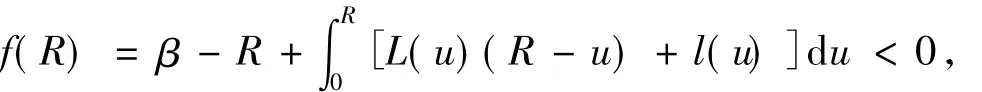
则方程f(t)=0有2个正根r1，r2，显然有r1＜R＜r2．引理1证毕．

引理2 设迭代序列{tn}满足

式(10)中，h(t)，g(t)由式(8)定义．则{tn}单调递增收敛到 r1．

证明 当 n=0 时，t1-t0=-(h'(t0)+［s0，t0;g］)-1(h(t0)+g(t0)) ＜ β．由 h(r1)+g(r1)=0，并根据式(8)，得 β＜ r1，则 t0＜t1＜r1．现假设 tk＜tk+1＜r1对 k≤n都成立．

当k=n+1时，

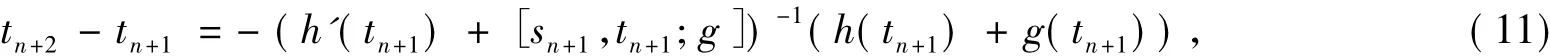
则由优函数表达式有：当 s，t∈(0，R)时，

当 t∈［0，r1)时，h(t)+g(t) ＞0．则由式(11)得 tn+1＜tn+2．因此，由归纳假设得{tn}单调递增．记 I(t)=t-(h'(t)+［s，t;g］)-1(h(t)+g(t))，显然 I(t)在［0，R)上是单调递增的，则 tn+1＜ tn+2=I(tn+1)≤I(r1)=r1．所以{tn}有极限，不妨记为 t*，显然 t*∈(0，r1］．现在证明 t*=r1．对迭代式

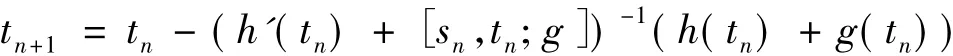
两边取极限，得h(t*)+g(t*)=0，即t*=r1．综上所述，{tn}单调递增收敛到r1．引理2证毕．

引理3 假设下列条件成立：

证明 当n=0时，以上5个结论显然成立．现设它们从0到n都成立，则根据条件2)和3)有

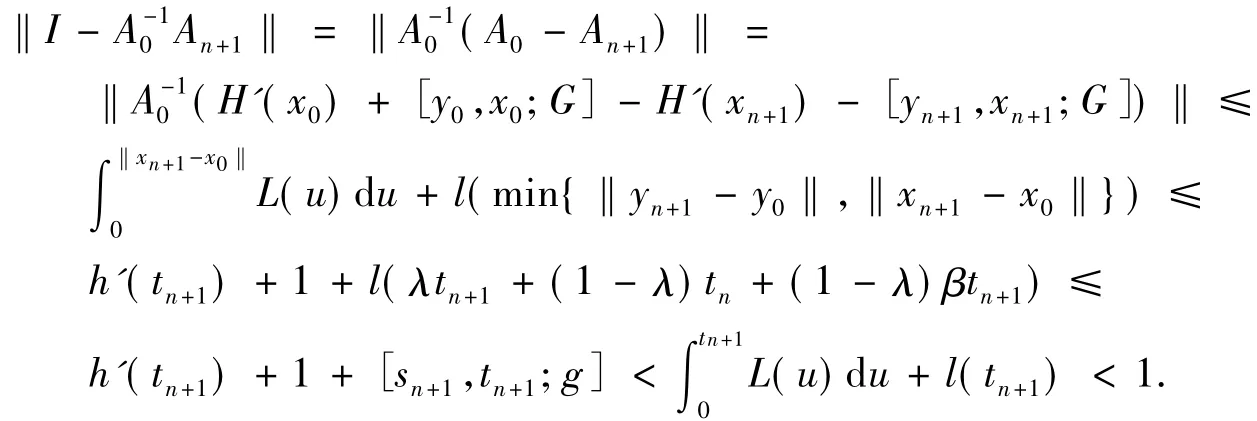
所以，根据Banach引理知A－1n+1存在，且结论2)成立．由迭代式(7)得

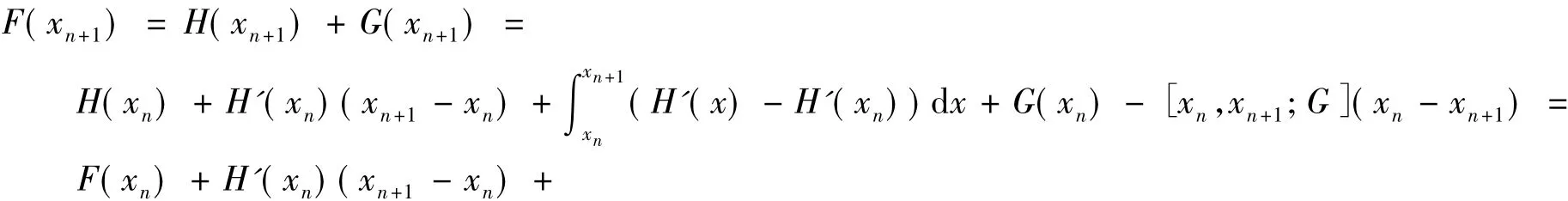
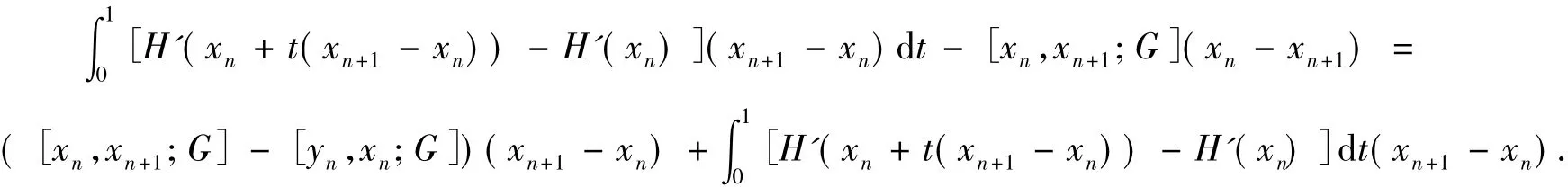
所以，根据条件3)和4)得

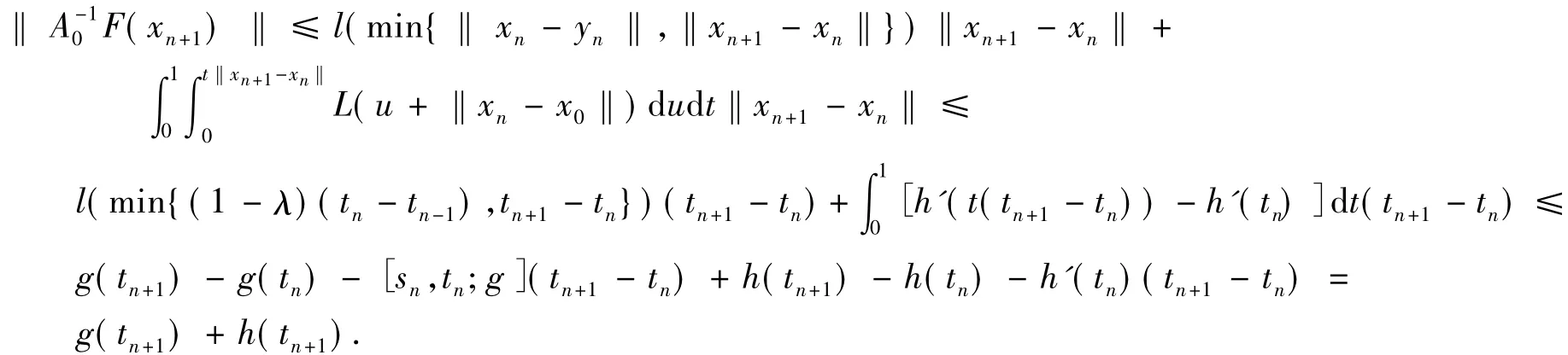
因此，结论3)对n+1成立．

根据结论1)，2)和3)可得

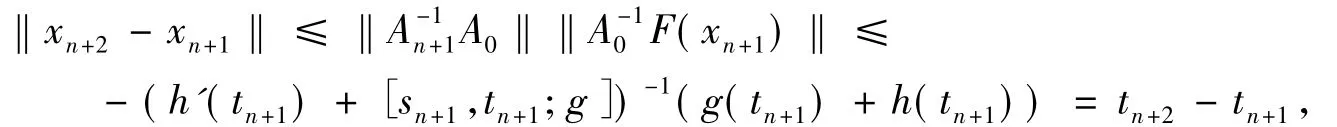
则结论4)对n+1成立．

由结论4)得

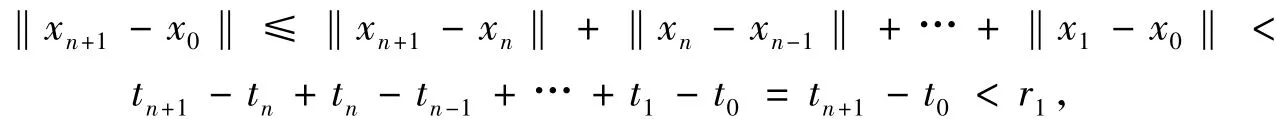
所以，结论5)对n+1成立．引理3证毕．

2 半局部收敛性

下面给出迭代算法(7)的半局部收敛性定理，并加以证明．

显然

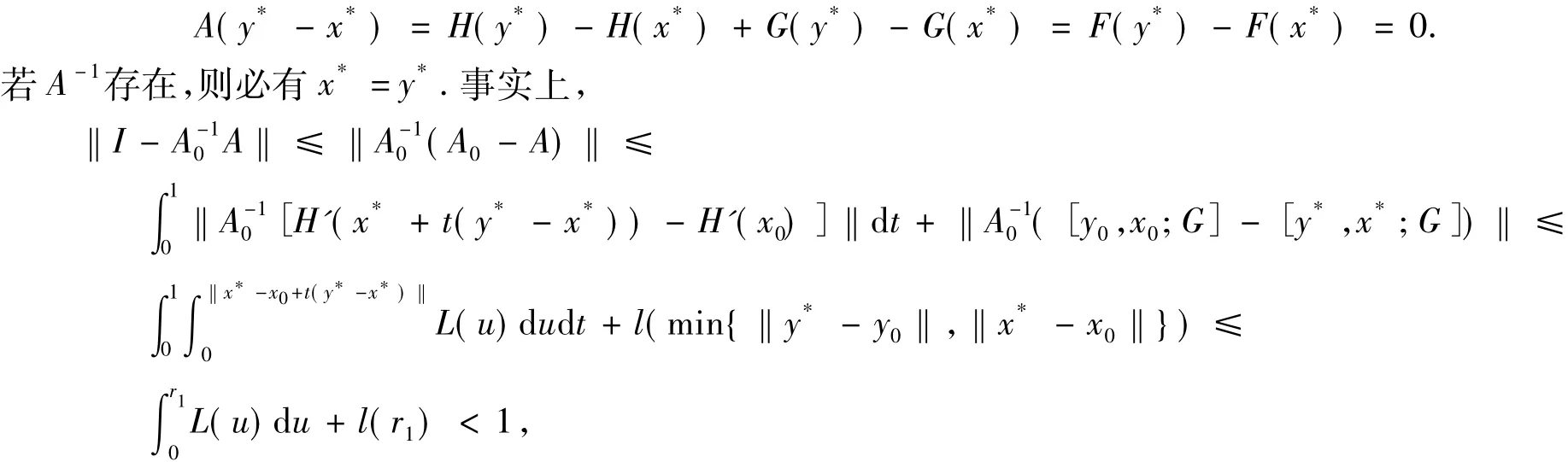
所以A-1存在．故x*=y*．定理1证毕．

3 应用

当G=0时，迭代式(7)就是牛顿迭代式．下面选择特殊的L和l对迭代式进行讨论．

推论1 对于常数 γ ＞0，0≤c＜1，取

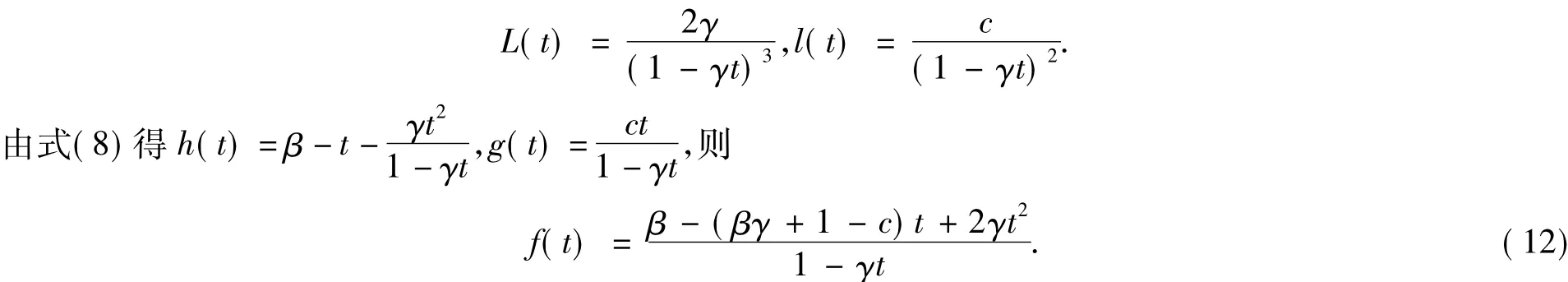
此时函数H和G满足

其中：

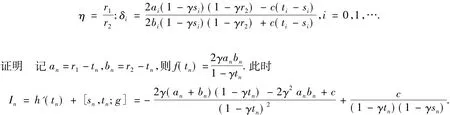
结合迭代式(10)，易得

类似可得

因此

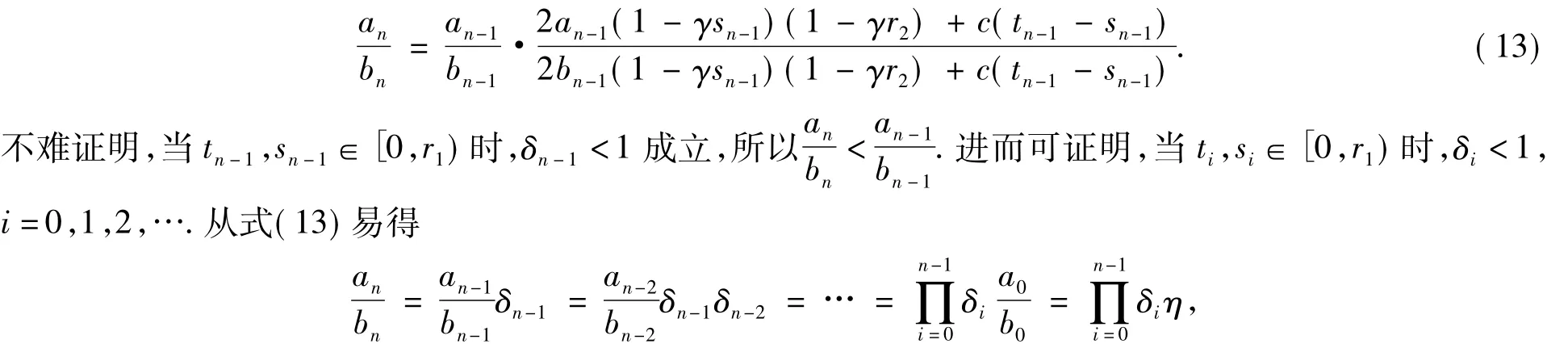
从而

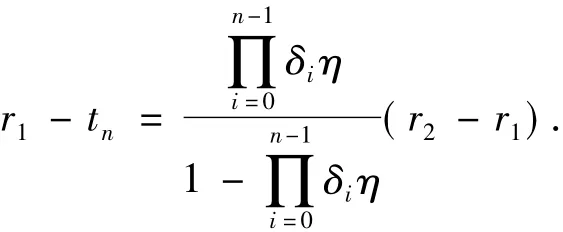
引理5证毕．

结合定理1和以上引理，可得到定理2．

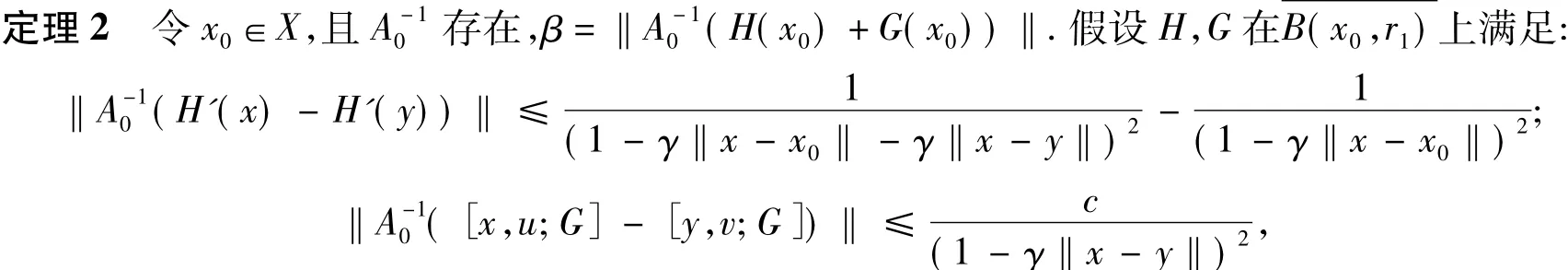
并满足

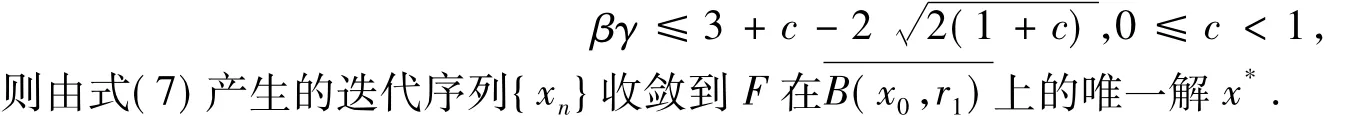
［1］Kantorvich L V，Akilov G P．Functional analysis［M］．Oxford：Pergamon Press，1982．

［2］Smale S．Newton's method estimates from data at one point［C］//Ewing R，Gross K，Martin C．The merging of disciplines：New directions in pure applied and computational mathematics．New York：Spring-Verlag．1986：185-196．

［3］Wang Xinhua．Convergence of Newton's method and inverse functions theorem in Banach space［J］．Math Comput，1999，68(225)：169-186．

［4］Argyros I K．On the solution of equations with nondifferentiable and Ptak error estimates［J］．BIT Numer Math，1990，30(4)：752-754．

［5］Zabreko P P，Nguen D F．The majorant method in the theory of Newton-Kantorovich approximations and Ptak error estimates［J］．Numer Func Anal Optimiz，1987，9(5/6)：671-684．

［6］Ren Hongmin．New sufficient convergence conditions of the secant method for nondifferentiable operators［J］．J Comput Math Appl，2006，182(2)：1255-1259．

［7］Hernández M A，Rubio M J．A uniparametric family of iterative process for solving nondifferentiable equations［J］．J Math Anal Appl，2004，275(2)：821-834．

［8］Catinas E．On some iterative methods for solving nonlinear equations［J］．Rev D'Analy Numér Theorie L'Approx，1994，23(1)：47-53．

［9］Hernández M A，Rubio M J．A modification of Newton's method for nondifferentiable equations［J］．J Comput Appl Math，2004，164/165(1)：409-417．