平面几何知识解决2013年高考解析几何问题的六个切入点
福建省宁德市民族中学 郑一平 (邮编:355000)
解析几何是高中数学的重点内容,也是高考考查的重要内容之一.它的特点是用代数方法研究解决几何问题,关键是用“数形结合”的思想把几何问题转化为代数问题.尤其是新课程改革增加了平面向量与导数之后,向量、导数与解几的交汇更成为高考的热点问题之一.这类问题涉及知识面广、综合性强、题目新颖、灵活多样,有时解题过程繁杂,许多学生经常出错.实际上涉及解析几何问题若能充分挖掘问题条件中隐含的几何特征,利用平面几何知识去解决,则能化难为易、化繁为简,收到意想不到的效果.下面从2013年高考试题谈平面几何在解析几何中的应用时的六个切入点.
1 以圆幂定理为切入点
例1 (2013年福建高考文科试题)如图1,抛物线E∶y2=4x的焦点为F,准线l与x轴的交点为A.点C在抛物线E上,以C为圆心,|OC|为半径作圆,设圆C与准线l交于不同的两点M、N.
(I)若点C的纵坐标为2,求|MN|;
(II)若|AF|2=|AM|·|AN|,求圆C的半径.
分析与略解 本题主要考查抛物线的方程、圆的方程与性质、直线与圆的位置关系等基础知识.问题(1)比较简单.问题(2)根据条件圆心C在抛物线上且过原点,按常规思路有标准答案中的解法:
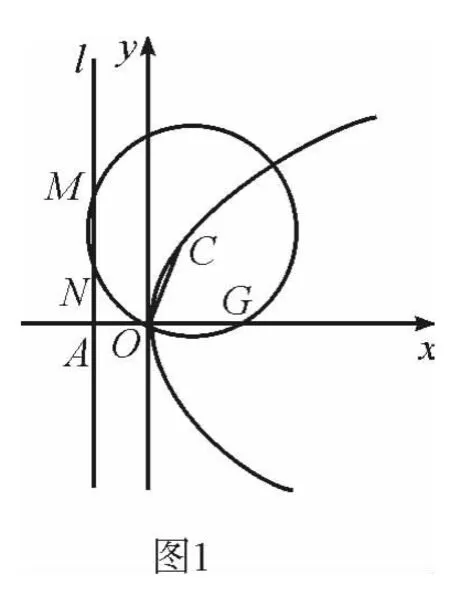
(Ⅰ)抛物线y2=4x的准线l的方程为x=-1,由点C的纵坐标为2,得点C坐标(1,2),所以点C到准线l的距离d=2,又|CO|=.所以
(Ⅱ)抓住圆的几何特征结合垂径定理,从圆幂定理为切入点有下列简洁解法:
设圆C与x轴交于不同的两点O、G.由圆幂定理知:|AO|·|AG|=|AM|·|AN|.
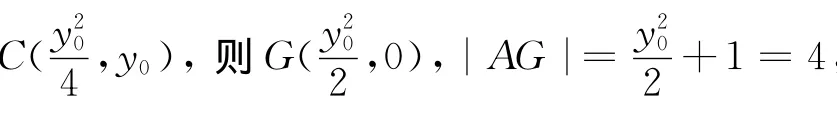
评析 涉及抛物线与圆的位置关系问题,关键要抓住圆心在抛物线上、圆过原点这些几何特征,结合垂径定理和根与系数关系得问题解.方(II)根据条件抓住几何特征通过圆幂定理解决,显然比标准答案所给的方法简单明了,关键就是充分利用了圆的几何性质化难为易、化繁为简,收到事半功倍的效果.下面再举数例说明:
2 以平面几何中面积比、线段比为切入点
例2 (2013年湖北高考试题)如图2,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m、2n(m>n),过原点且不与x轴重合的直线l与C1、C2的四个交点按纵坐标从大到小依次为A、B、C、D.记λ=m,△BDM和△ABN的面积分别为S1和S2.
(Ⅰ)当直线l与y轴重合时,若S1=λS2,求λ的值;
(Ⅱ)当λ变化时,是否存在与坐标轴不重合的直线l,使得S1=λS2?并说明理由.
分析与略解 根据条件涉及线段的比以及三角形面积问题,因此抓住图形间的几何关系从线段成比例为切入点思考比较佳.
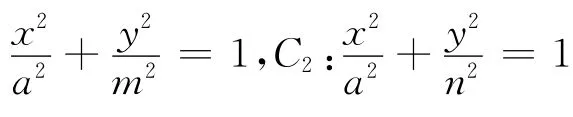
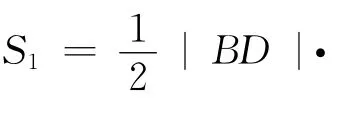
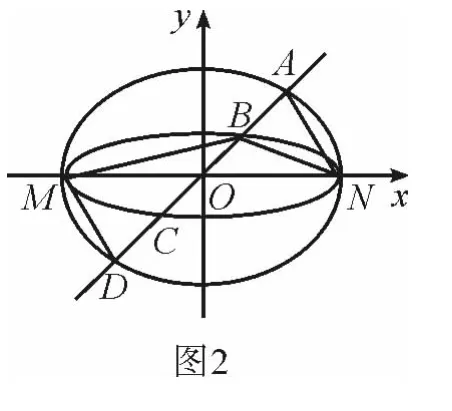
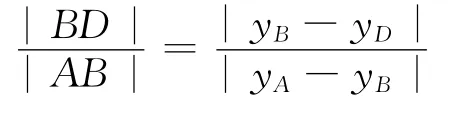
故当直线l与y轴重合时,若S1=λS2,则λ=+1.
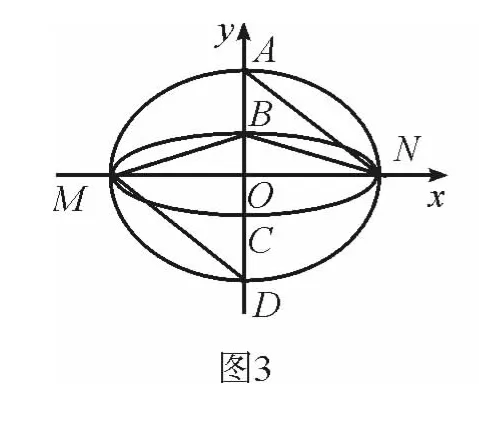
解法2 如图3,若直线l与y轴重合,则|BD|=|OB|+|OD|=m+n,|AB|=|OA|-|OB|=m-n.
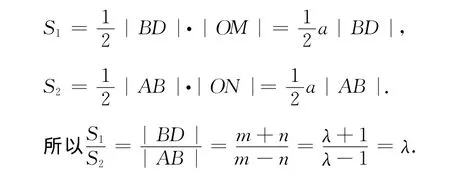
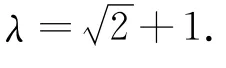
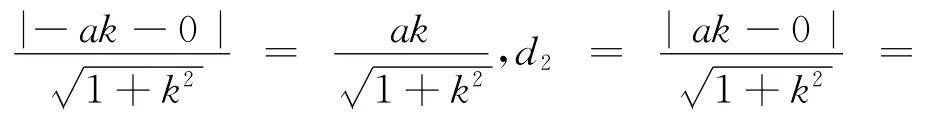

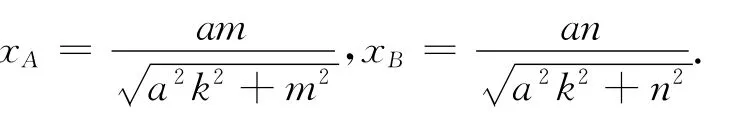
根据对称性可知xC=-xB,xD=-xA,于是

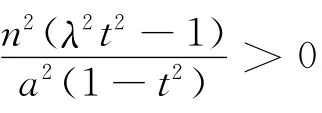
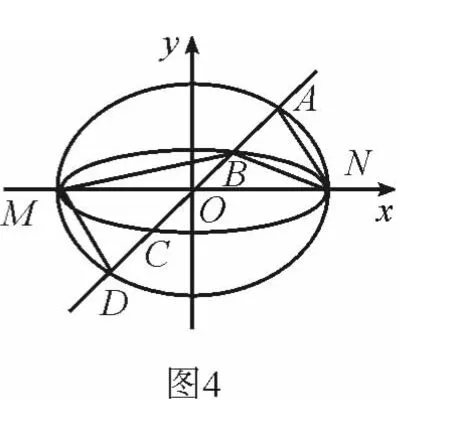
解法2 如图4,若存在与坐标轴不重合的直线l,使得S1=λS2.根据对称性,
不妨设直线l:y=kx(k>0),点M(-a,0),N(a,0)到直线l的距离分别为d1、d2,则
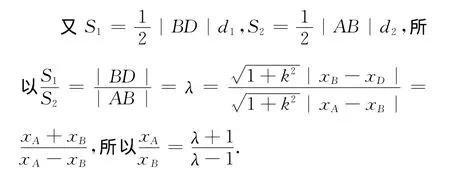
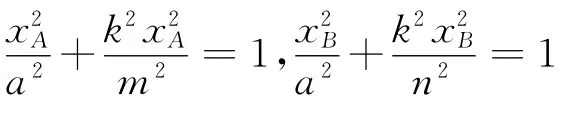
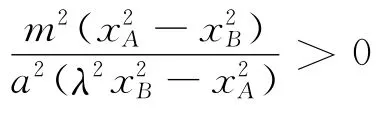
评析 本题若能通过条件结合图形抓住三角形面积与边或高的关系,利用比例推理计算求得结果,过程涉及点到直线距离和弦长等公式的应用,通过图形中的几何特征的挖掘发现解题思维突破口是解题的关键.
3 以两圆圆心距与两半径间的位置关系为切入点
例3 (2013年高考新课标卷I)已知圆M:(x+1)2+y2=1,圆N∶(x-1)2+y2=9,动圆P与M外切且与圆N内切,圆心P的轨迹为曲线C.
(Ⅰ)求C的方程;
(Ⅱ)l是与圆P,圆M都相切的一条直线,l与曲线C交于A,B两点,当圆P的半径最长时,求|AB|.
分析与略解 由已知得圆M的圆心为M(-1,0),半径r1=1,圆N的圆心为N(1,0),半径r2=3.设动圆P的圆心为P(x,y),半径为R.
(Ⅰ)由圆P与圆M外切且与圆N内切1即|PM|+|PN|=(R+r1)+(r2-R)=r1+r2=4,由椭圆的定义可知,曲线C是以M、N为左右焦点,长半轴长为2,短半轴长为的椭圆(左顶点除外),其方程为
(Ⅱ)对于曲线C上任意一点P(x,y),由于|PM|-|PN|=2R-2≤2,即R≤2,当且仅当圆P的圆心为(2,0)时,R=2.所以当圆P的半径最长时,其方程为(x-2)2+y2=4,当l的倾斜角为90°时,l与y轴重合,可得|AB|=2.
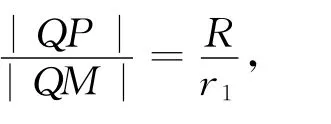
评析 涉及圆与圆、圆与直线位置关系问题抓住圆的几何特征,结合垂径定理、点线距离、弦长公式等沟通条件与结论间的关系是解决问题的关键.
4 以向量的几何意义为切入点
例4 (2013年上海市春季高考试题)已知抛物线C:y2=4x的焦点为F.
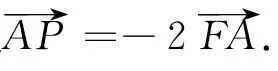
(2)在x轴上是否存在点Q,使得点Q关于直线y=2x的对称点在抛物线C上?如果存在,求所有满足条件的点Q的坐标;如果不存在,请说明理由.
分析与略解 由条件直接利用向量的几何意义求解.(1)设动点P的坐标为(x,y),点A的坐标为(xA,yA),则= (x-xA,y-yA),因为F的坐标为(1,0),所以= (xA-1,yA),由=-2得(x-xA,y-yA)=-2(xA-1,yA).
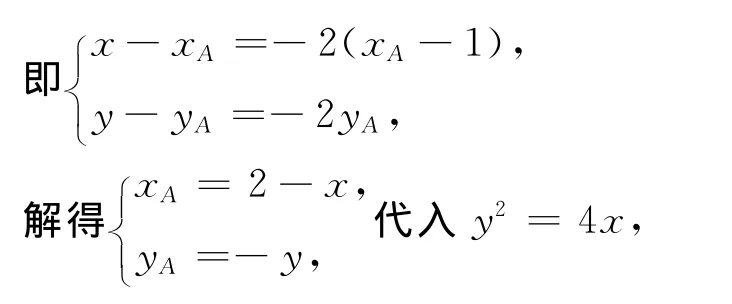
得到动点P的轨迹方程为y2=8-4x.
(2)设点Q的坐标为(t,0).点Q关于直线y=2x的对称点为Q′(x,y),

若Q′在C上,将Q′的坐标代入y2=4x,得4t2+15t=0,即t=0或t=-.所以存在满足题意的点Q,其坐标为(0,0)和(-,0).
5 以特殊三角形的性质、几何特征为切入点
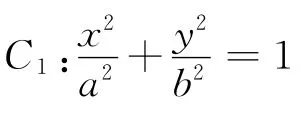
(Ⅱ)记直线AP、BP、AQ、BQ的斜率分别是k1、k2、k3、k4,求证:k1·k2+k3·k4为定值;
(Ⅲ)过Q作垂直于x轴的直线l,直线AP、BP分别交l于M、N,判断△PMN是否可能为正三角形,并说明理由.
分析与略解 本题考查直线、椭圆、双曲线等基础知识,考查运算求解能力和探究能力,数形结合思想、化归与转化思想.

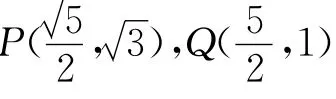
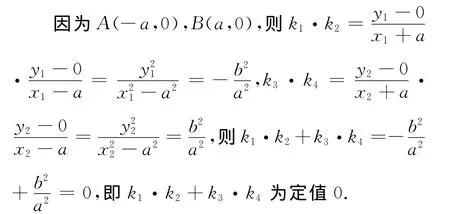
(Ⅲ)解法1 由条件假设△PMN为正三角形,下面分点P在x轴上方和下方两种情况:
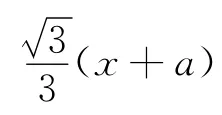
综合上述,当a=且点P为椭圆的顶点(0,b)或(0,-b)时,△PMN为正三角形.
解法2 分析条件中隐含的几何特征,考虑用等腰三角形两底角相等几何性质处理:假设△PMN为正三角形,则 ∠MPN= ∠PMN=60°,又MN⊥x轴,则 ∠PAB=30°,∠PBA=30°,即ΔPAB为等腰三角形.

综合上述,当a=且点P为椭圆的顶点(0,b)或(0,-b)时,△PMN为正三角形.
评析 显然问题(III)的解法2过程直观简洁,避免了分类讨论和计算.关键就在于抓住了等腰三角形的几何特征.
6 以圆锥曲线的几何意义为切入点
例6 已知动圆A经过点B(1,0),且和直线x+1=0相切.(1)求圆心A的轨迹E方程;(2)设点P(x0,y0)为曲线E上的任意一点,点M的坐标为(x0+2,0),过点M作直线PB的垂线,垂足为N,当x0变化时,线段PN的长度是否为定值?若是,请写出这个定值,并证明你的结论;若不是,请说明理由.
分析与略解 本小题主要考查抛物线的标准方程与性质、直线的方程及其位置关系、点到直线的距离公式等基础知识,考查推理论证能力、运算求解能力,考查函数与方程思想、化归与转化思想、分类与整合思想.
(I)解法1 (定义法)依题意,由抛物线定义知,轨迹E是以B(1,0)为焦点,直线x=-1为准线的抛物线,所以轨迹E的方程是y2=4x.

所以轨迹E的方程是y2=4x.
(II)线段PN的长度为定值2,证明如下:
解法1 当x0=1时,点P(1,±2),PB⊥x轴,点N与点B重合,|PN|=|PB|=2.
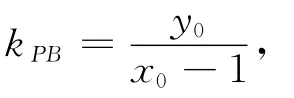
综上,线段PN的长度为定值2,

综上,线段PN的长度为定值2.
解法3 (几何法)当x0=1时,点P(1,±2),PB⊥x轴,点N与点B重 合,|PN|=|PB|=2.当y0=0时,点P(0,0),点M(2,0),点N与点M重合.|PN|=|PM|=2.当x0≠1且y0≠0时,过点P作PH⊥x轴于H,则|MH|=2.
因为|PB|=x0+1,|MB|=x0+1,,所以|PB|=|MB|,所以RtΔPBH≌RtΔMBN.得|BH|=|BN|,因此|PN|=|MH|=2.
综上,线段PN的长度为定值2.
以上可以看出,平面几何在解析几何中有着广泛的应用,在解题中要有几何意识,善于挖掘条件中隐含的几何因素,结合有关知识去解决.

