（2+1）维非线性发展方程的对称约化及精确解

李宁, 刘希强, 张颖元

（2+1）维非线性发展方程的对称约化及精确解

*李宁, 刘希强, 张颖元

（聊城大学数学科学学院，山东，聊城 252059）

利用相容性方法，得到了(2+1)维mKdV-KP的非经典对称及相似约化，并进一步得到了该方程的一些新的精确解，包括双曲函数解，三角函数解，有理函数解，椭圆函数解等。

相容性方法；(2+1)维mKdV-KP方程；精确解；对称；相似约化

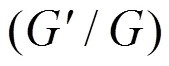
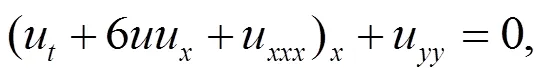
即

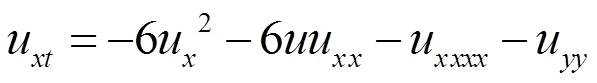
方程(2)的显式解。(2+1)维mKdV-KP方程是基于(2+1)维KdV和(2+1)维KP方程提出的推广。 A. S. Al-Fhaid利用F展开法[10]得到了该方程的雅可比双周期波解，N Taghizadeh等用首次积分法[11]得到了该方程的行波解。文献[4]中作者利用修正的CK直接方法得到了非线性发展方程的对称，从而约化方程，但此方法需要复杂的计算和转化过程。文献[6]中作者利用经典李群方法得到了非线性发展方程的李点对称，也达到约化方程的目的，但此方法在求解生成元时需大量的计算。虽然相容性方法的最终目的同样是寻找非线性发展方程的对称，但该方法能够简化计算过程，并能得到更多新的结果。本文的求解过程恰能说明相容性方法的优越性。

相容性方法的主要思想是假定方程(2)有如下形式

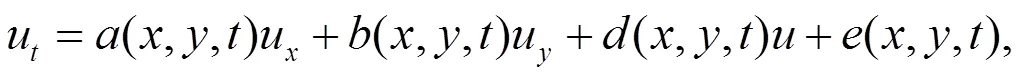
1 (2+1)维mKdV-KP方程的非经典对称

把(3)式带入(2)式，得到

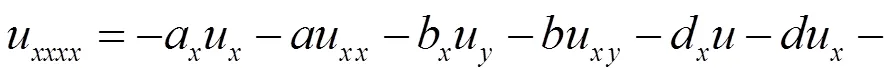
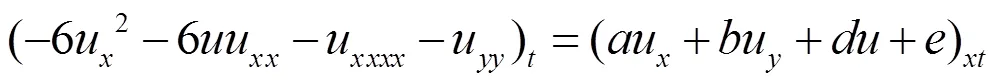
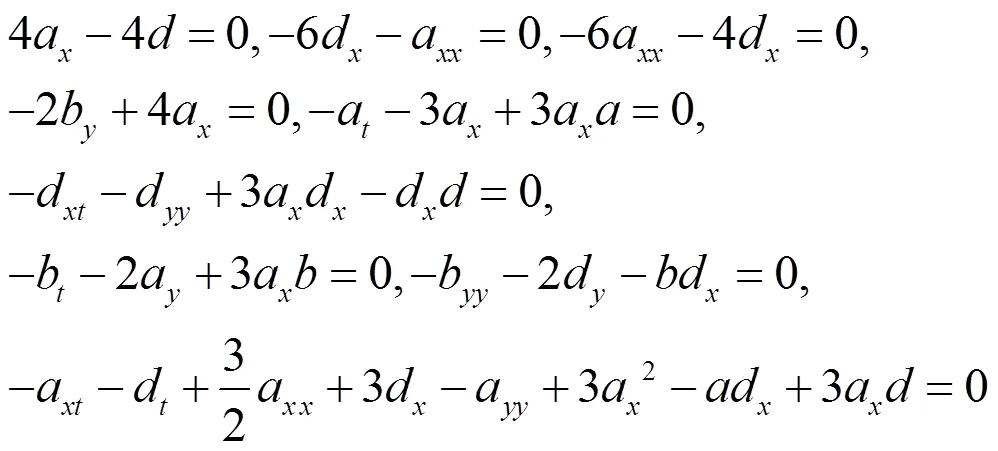
解上述超定方程组可得

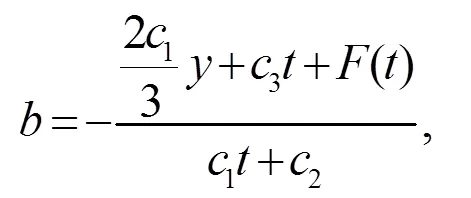
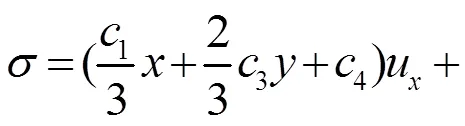
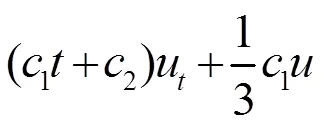
2 (2+1)维mKdV-KP方程的对称约化以及显式解

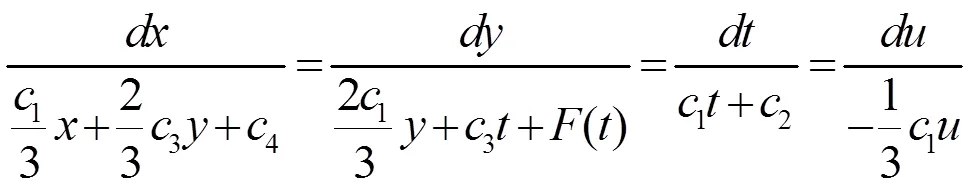
分以下3种情况讨论：

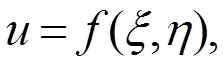
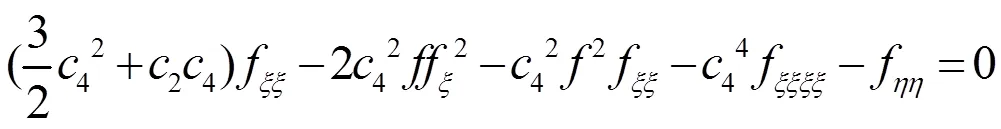
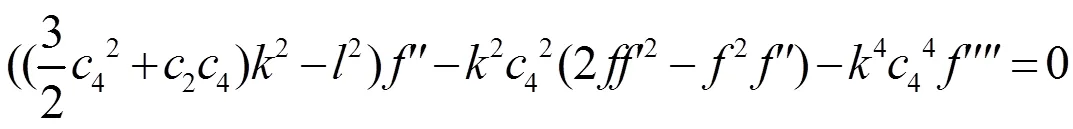
以下用扩展的tanh方法求解方程(12)。假设方程(12)有以下形式的解

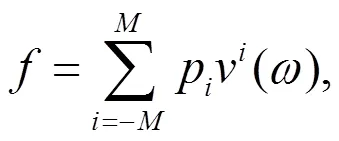
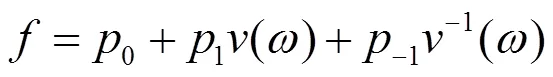
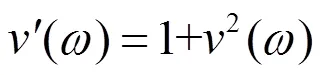
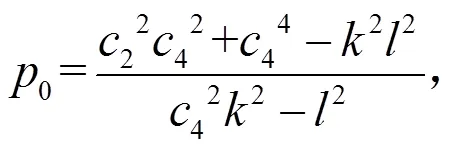
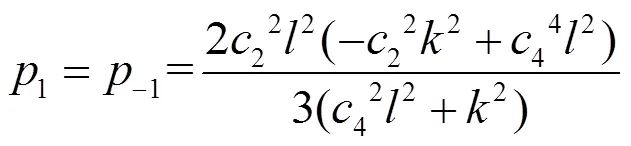
则方程(12)的解为

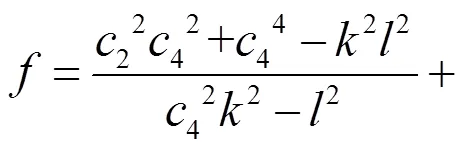
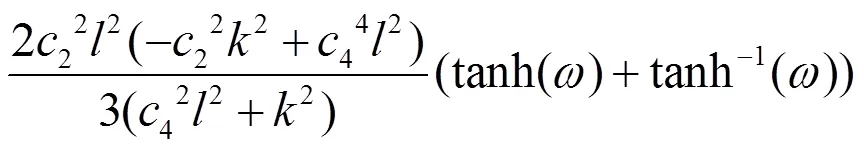
即原方程(2)的解为

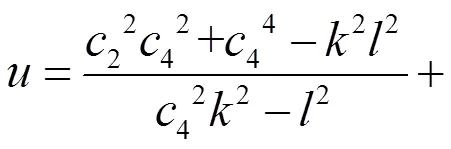
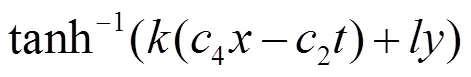
为了得到方程(2)更广泛的解，将(12)式积分两次可以得到

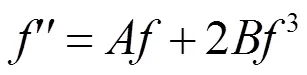
由(19)式容易得到

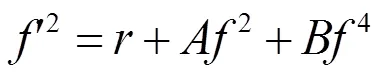
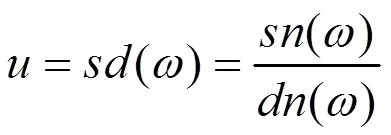
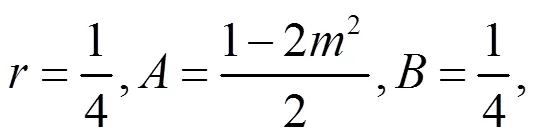
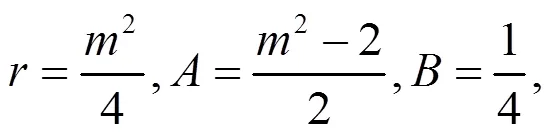
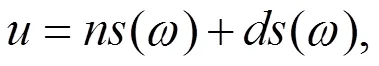
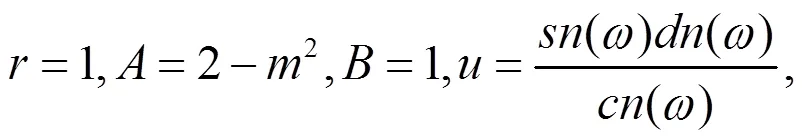
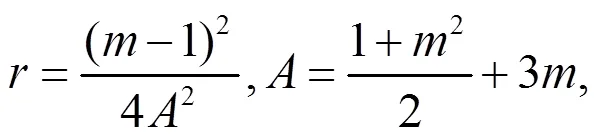
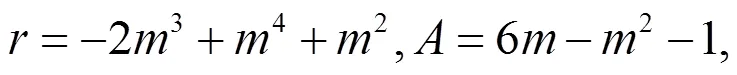
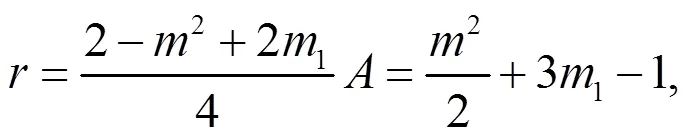
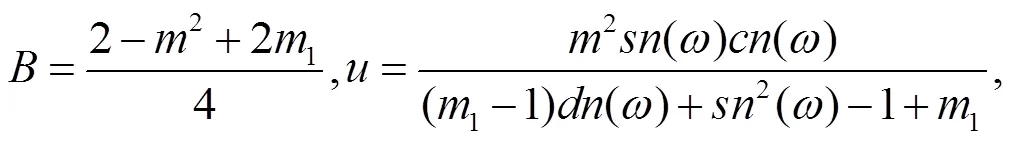
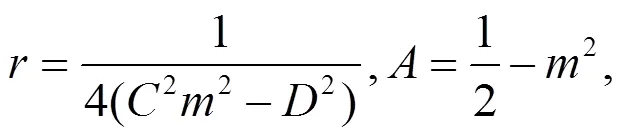
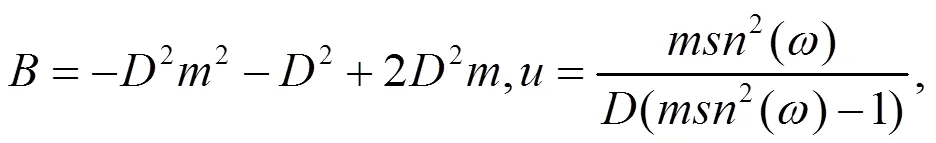
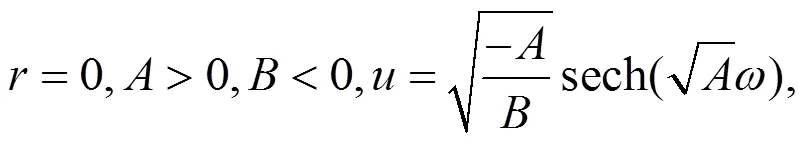
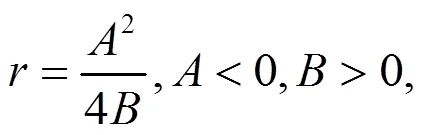
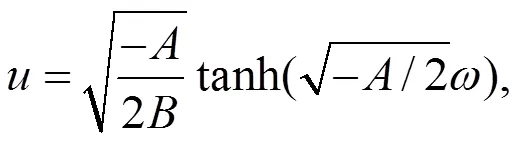
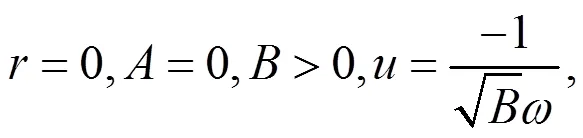
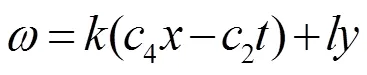
注1：情况1 中还有大量解，这里不再一一列出，而且都是新解。

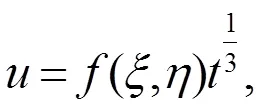
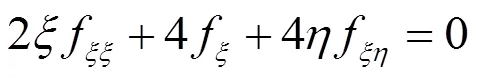
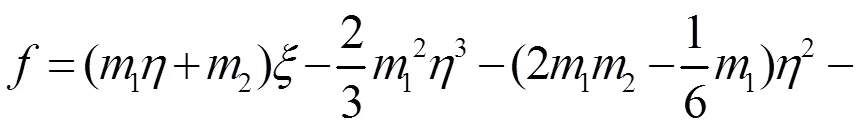
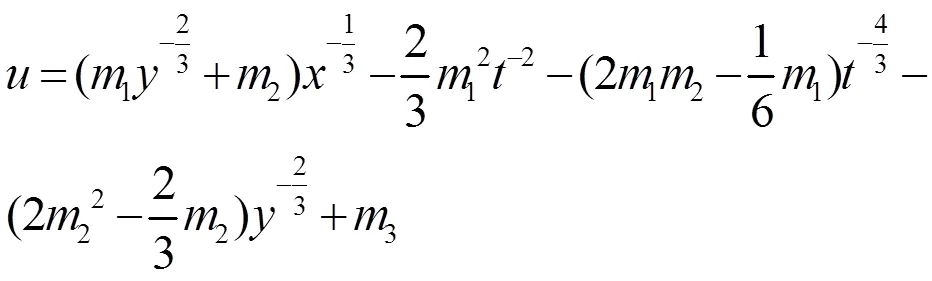
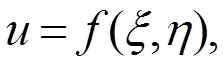
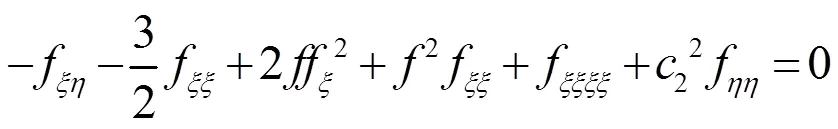
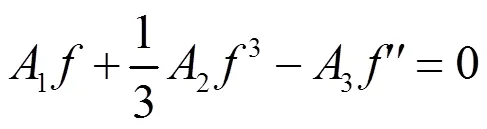
以下借助辅助函数[13]来求解方程(23)的解。设方程(23)有以下形式的解

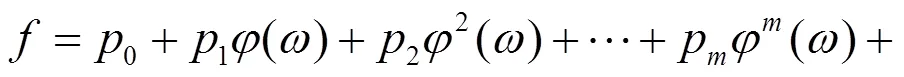
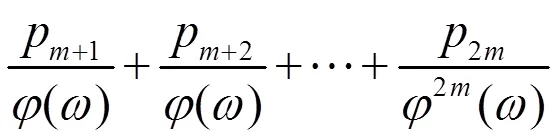
利用辅助方程

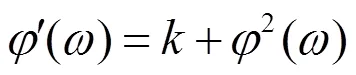
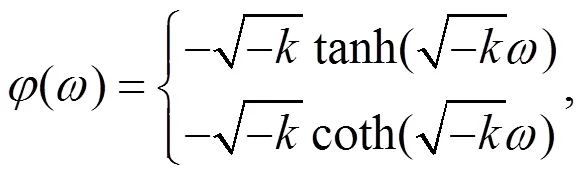
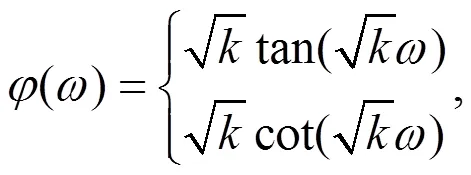
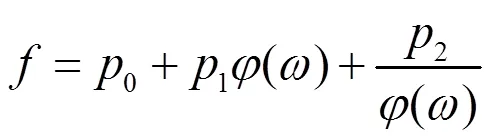
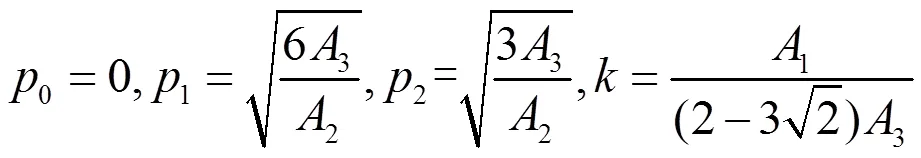
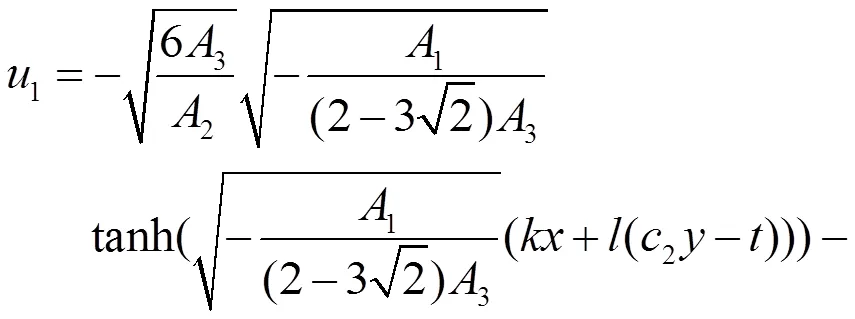
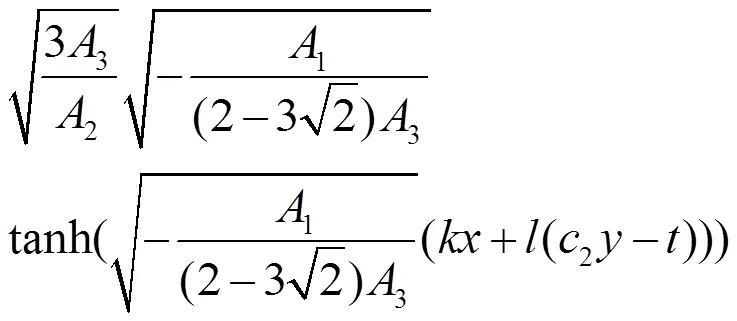
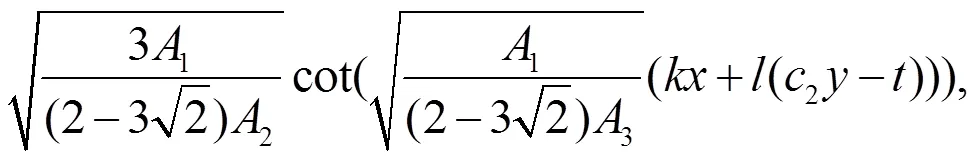
方程(22)也可以约化为

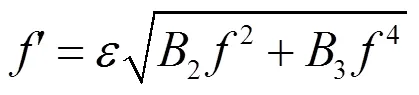
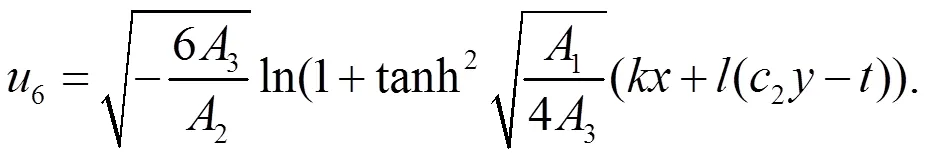
注2：经过Maple数学软件验证情况3中的6组解都是方程(2)的解，而且均是新解。

3 结论

利用相容性方法得到了mKdV-KP方程的非经典对称，并利用其得到了该方程的相似约化，通过解约化方程得到了mKdV-KP方程的一些精确解。

[1] Ye Caier. New Exact Solutions for the Generalized mKdV Equation with Variable Coefficients[J]. Applied Mathematical Sciences,2011,5(75): 3715-3721.

[2] Gai Xiao-ling, Gao Yi-tian, Meng De-xin, et al. Darboux Transformation and Soliton Solutions for a Variable Coefficient Modified Kortweg-deVries Model from Fluid Mechanics, Ocean Dynamics, and Plasma Mechanics [J]. Commun. Theor. Phys., 2010,53(4): 673- 678.

[3] Rady A S , Osman E S. Multiple soliton for the system of coupled KdV equations[J]. Appl.Math. Comput., 2009 (210): 177-181.

[4] 张琳琳,辛祥鹏.(2+1)维修正KP方程的精确解[J]. 聊城大学学报：自然科学版,2009,22(3):9-13.

[5] 刘文健，刘希强,桑波.非线性发展方程的新精确解[J].西北师范大学学报：自然科学版,2012,48（2）:31-36.

[6] 王刚伟，刘希强，张颖元.变系数mKdV方程的精确解[J].井冈山大学学报：自然科学版，2012,33(5):1-5.

[8] Wazwaz A M. Solitons and singular solitons for the Gardner-KP equation[J]. Appl. Math. Comput, 2008 ,204:162- 169.

[9] Liu Na, Liu Xi-qiang, Similarity reduction and solutions of the (3+1)-dimensional Kadomtsev- petviashvili equation[J].Phy Lett A,2008,25:3527- 3530.

[10] Al-Fhaid A S. [PDF]New exact solutions for the modified KdV-KP equation using the extended F-expansion method[J]. Applied Mathematical Sciences,2012,6: 5315- 5332.

[11] Taghizadeh N, Mirzazadeh M , Farahrooz F. The first integral method for some time fractional differential equations[J]. Appl. Math. Model, 2011,35: 3991.

[12] Bai Cheng-lin, Bai Cheng-jie , Zhao Hong. A new generalized algebraic method and its application in nonlinear evolution equations with variable coefficients [J]. Z. Naturforsch, 2005, 60a: 211-220.

[13] Yan Zhen-ya. The Riccati equation with variable coefficients expansion algorithm to find more exact solutions of nonlinear differential equations Computer Physics Communications 2003,152:1-8.

[14] Huang Ding-jiang, Li Deng-sheng , Zhang Hong-qing. Explicit and exact traveling wave solutions for the generalized derivative Schrödinger equation [J]. Chaos, solitions and Fractals,2007,31:586-593.

SYMMETRY REDUCTIONS AND EXACT SOLUTIONS OF (2+1)-DIMENSIONAL NONLINEAR EVOLUTION EQUATION

*LI Ning，LIU Xi-qiang，ZHANG Ying-yuan

(School of Mathematical Sciences, Liaocheng University, Liaocheng, Shandong 252059, China)

Based on the compatibility method, we find the non-classical symmetry, reductions and new exact solutions of mKdV-KP equation including the hyperbolic functions, the trigonometric functions, the rational functions and the elliptic functions and so on.

the compatibility method; (2+1)-dimensional mKdV-KP equation; exact solutions; symmetry; similar reduction

O175. 2

A

10.3969/j.issn.1674-8085.2013.03.002

1674-8085(2013)03-0005-05

2012-11-21；

2013-03-14

国家自然科学基金和中国工程物理研究院联合基金项目(11076015)

*李 宁(1981-），男，山东枣庄人，硕士生，主要从事非线性偏微分方程解的研究(E-mail:ln1011@163.com);

刘希强(1957-)，男，山东菏泽人，教授，博士，主要从事非线性微分方程系统研究(E-mail: liuxiq@sina.com);

张颖元(1987-)，女，山东济南人，硕士生，主要从事非线性偏微分方程解的研究(E-mail:zhangyingyuanok@126.com).