局部次高斯随机序列算术平均的强偏差定理
张怀举,吴 玉,范爱华
(安徽工业大学数理学院,安徽马鞍山243032)
诸多有用的统计模型皆基于随机样本的加权和或部分和,因而研究随机变量序列部分和平均的极限性质,显得尤其重要。研究者们对于独立与混合相依随机序列部分和平均的渐近性质进行了大量研究,如Gaposhkin[1]讨论了独立同分布随机变量序列滑动平均的极限定理;Lai[2]研究了独立随机序列的求和法;Jain[3]讨论了独立Banach空间随机元部分和的尾概率;Mason[4]推广了Erdos-Renyi强大数定律。20世纪70年代末,刘文教授在研究实数展式的概率性质时,提出了一种研究强极限定理的新方法—函数论方法[5]。随后,刘文教授又将这种方法和矩母函数与鞅方法结合起来[6-7],扩大了该方法的应用范围。在其后的研究中,汪忠志等[8]通过引进似然比作为随机变量序列相对于不同测度的差异的一种度量,利用这种方法得到了一类用不等式表示的强极限定理,即强偏差定理。此后,杨光等对相依序列无规则性的强偏差定理进行了研究[9]。受此启发,本文引入相对熵的概念,借助纯分析的方法,研究局部次高斯随机序列部分和算术平均的强偏差定理,推广了已知的结果。
1 预备知识
设{Xn,n≥1}是定义在概率空间(Ω ,ℱ,μ)上的随机序列,其联合分布密度函数为

若{Xn,n≥1}关于另一测度下是独立的,其密度函数是 pi(xi),i=1,2,…。令
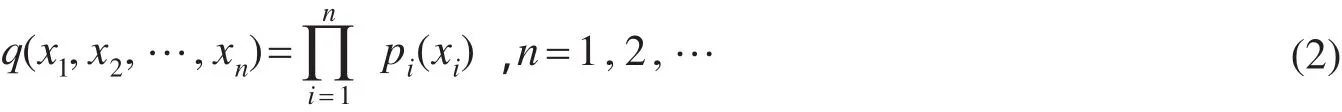
定义1 称随机变量 Xi是局部次高斯随机变量,若存在常数νi∊R,αi∊[0,∞)和 δi∊(0,∞ ],使得对t∊(-δi,δi) ,都有

定义2[10]称随机变量Xi是次高斯随机变量,如果存在一非负实数αi,使得对任意的t∊R,都有

其中,可以看出次高斯随机变量是局部次高斯随机变量参数取νi=0和δi=∞时的情形,令

为了刻画{Xn,n≥1}的一般情形(关于测度μ)与乘积分布(关于测度)之间的差异,引入
定义3 设{Xn,n≥1} 是具有联合分布密度(1)、(2)的随机序列,称

定义4 设{Xn,n≥1}是具有联合分布密度(1)、(2)的随机序列,Λn(ω)是此随机序列相对于参考乘积分布的似然比,称

为{Xn,n≥1}的相对熵或渐近对数似然比。
2 主要结论
引理1[11]设 p(x1,x2,…,xn)和 q(x1,x2,…,xn)是 (Ω,ℱ )上的两个联合分布密度函数,则


则

证明 假设t是任意的实数,令

可知构造的 q(t;x1,x2,…,xn)是 ( )Ω,ℱ 上的n维概率密度函数。定义

于是引理1可改写为

由于
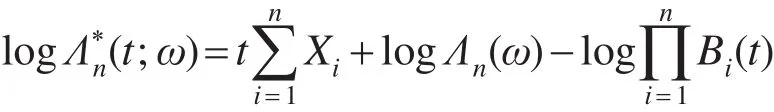
得

由式(3)和(16)有
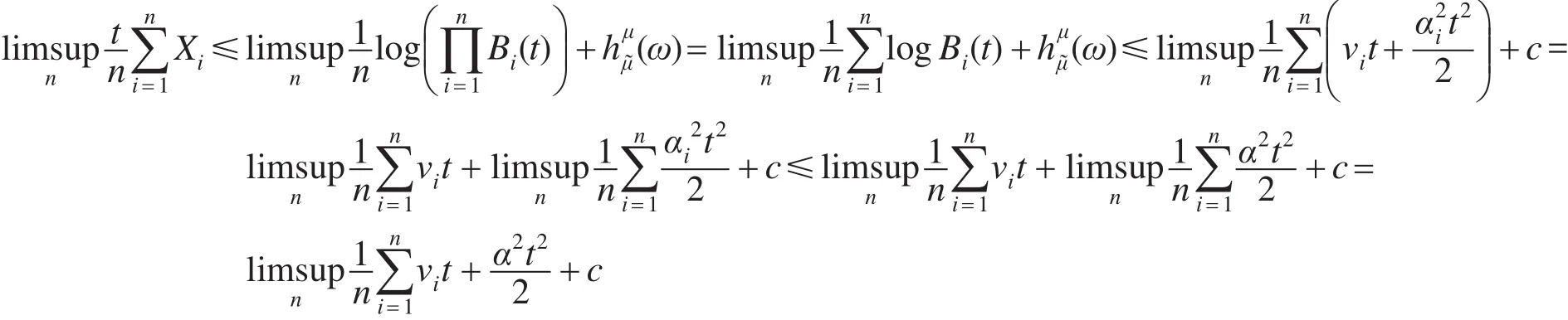
令t<0,则由上式得
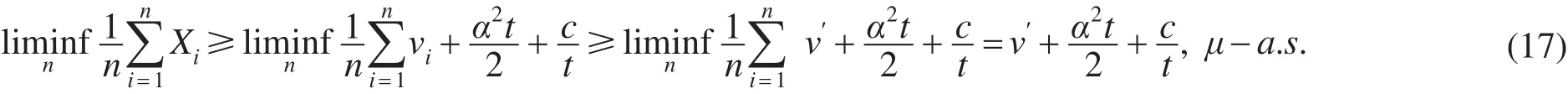
即

式(9)成立,类似地,令t>0,则有
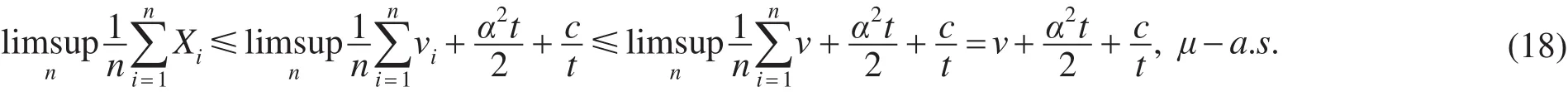
即

式(10)成立。
推论1设{Xn,n≥1} 是一次高斯随机序列,Λn(ω),hμ(ω),H(c)定义见式(5),(6)及(8),c≥0 为常数,则
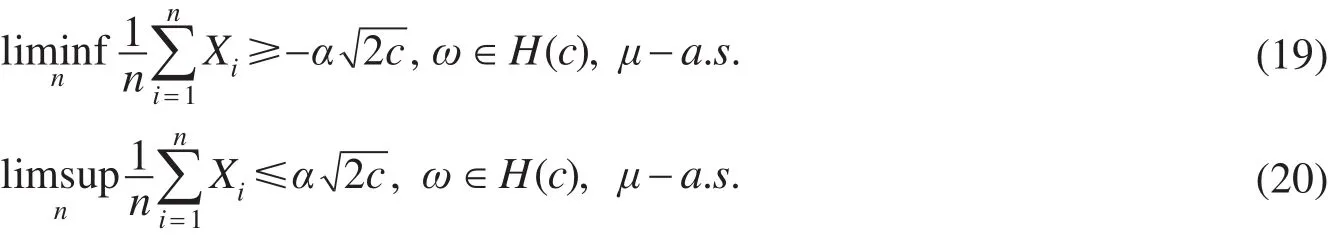
证明 利用定理1中证明的式(16),结合式(4)及式(6),即得

令t<0,则由上式得

即
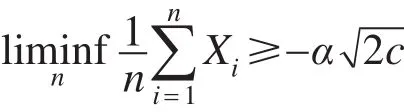
式(19)成立。令t>0,同理证得式(20)成立。
进一步,若当{Xn,n≥1}在下是相互独立的且同分布的随机序列时,有推论2和3。
推论2 设{Xn,n≥1}是一局部次高斯随机序列,且在下是相互独立的且同分布,即假设{Xn,n≥1} 在测度下的联合分布为
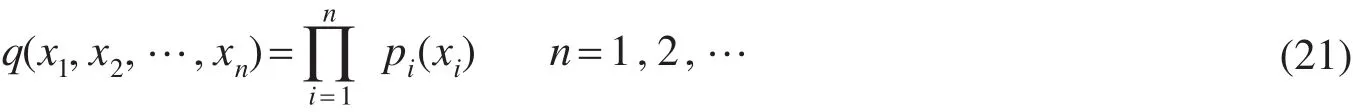
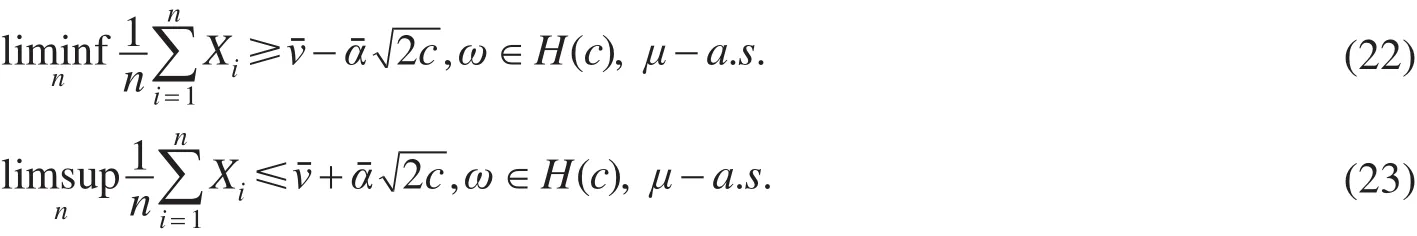
推论3 设{Xn,n≥1}是一次高斯随机序列,且在下是相互独立的且同分布,即假设{Xn,n≥1} 在测度下的联合分布为

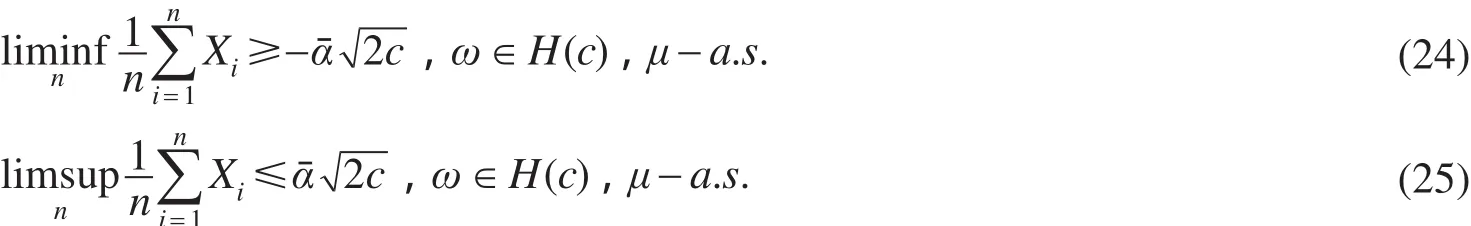
[1]Gaposhkin V F.The law of large numbers for moving averages of independent random[J].Mathematicheskie Zametki,1987,42(1):124-131.
[2]Lai T L.Summability methods for independent identically distributed random variables[J].Proceedings of theAmerican Mathematical Society,1974,45(2)253-261.
[3]Jain N C.Tail probabilities for sums of independent Banach space valued random variables[J].Zeitschrift für Wahrscheinlichkeitstheorie und Verwandte Gebiete,1975,33:155-166.
[4]Mason D M.An extended version of the Erdos-Renyi strong law of large numbers[J].TheAnnals Probability,1989,17(1):257-265.
[5]刘文.强偏差定理与分析方法[M].北京:科学出版社,2003.
[6]Liu W.Aclass of strong deviation theorems and an approach of Laplace transformation[J].Chinese Science Bulletin,1998,43(19):1605-1610.
[7]Liu W,Wang Y J.A class of strong deviation theorems for the sequences of absolutely continuous random variables[J].Acta Mathematica Scientia,2001,21A(1):23-28.
[8]汪忠志,杨卫国.关于相依离散随机序列的若干强偏差定理[J].系统科学与数学,2011,31(8):932-942.
[9]杨光,陈文波.相依随机序列的若干强偏差定理[J].安徽工业大学学报:自然科学版,2013,30(2):182-186.
[10]沈阳,张怀举,范爱华.关于次高斯随机序列的一类强偏差定理[J].安徽工业大学学报:自然科学版,2012,29(3):276-279.
[11]范爱华.样本相对熵与相依随机序列的若干小偏差定理[J].兰州大学学报:自然科学版,2008,44(1):128-136.

