The analysis of second-order sloshing resonance in a 3-D tank*

ZHANG Hong-sheng (张洪生), WU Peng-fei (吴鹏飞), LIU Wen-bai (刘文白)

College of Ocean Science and Engineering, Shanghai Maritime University, Shanghai 201306, China, E-mail: hszhang@shmtu.edu.cn

The analysis of second-order sloshing resonance in a 3-D tank*

ZHANG Hong-sheng (张洪生), WU Peng-fei (吴鹏飞), LIU Wen-bai (刘文白)

College of Ocean Science and Engineering, Shanghai Maritime University, Shanghai 201306, China, E-mail: hszhang@shmtu.edu.cn

(Received November 2, 2013, Revised January 17, 2014)

Based on the potential theory and perturbation techniques, the problem of second-order sloshing in a three-dimensional tank in combination with surge and sway motions is analyzed. When excitation is applied in both horizontal directions, the second-order resonance can occur when the sum frequency or the difference frequency of any two excitation components is equal to one of the natural frequencies. The resonance can also occur when the sum or difference frequency of one of the excitation frequencies and one of the natural frequencies is equal to another natural frequency.

sloshing, second-order resonance, three dimensions, coupling terms

Introduction

Resonance is a very important phenomenon in nature. It occurs when the external excitation frequency is equal to one of the natural frequencies of the system, which may lead to its excessive response. One of the typical examples of resonance is sloshing in a tank that is partially filled with liquid and plced on an ocean going ship. A large amount of work has been done on the sloshing resonance. Faltinsen[1]used the linear inviscid theory to solve the problem of sloshing in a tank with two-dimensional flow. When the motion frequency of the tank is equal to one of the natural frequencies, the amplitude of wave in the tank tends to infinity as time increases. Sloshing problems have also been solved by the fully nonlinear theory. Typical publications include those by Wu et al.[2]and Wang and Khoo[3]using the finite element method, by Huang et al.[4]using the high-order finite element method, by Faltinsen and Timokha[5]using the nonlinear modal analysis, and by Hu et al.[6]and Ma et al.[7,8]using the time domain analysis. The elevation of the free surface at resonance from the nonlinear theory may not tend to infinity but still remain exceedingly large. This may still cause violent impact on the tank leading to damage.

More recently Wu[9]has noticed that in addition to the first-order resonance, the second-order resonance can also occur. The relevance of the second-order resonance was then confirmed by Wang et al.[10]who analyzed the motion of the liquid confined between floating cylinders based on the fully nonlinear theory. Chern et al.[11]confirmed the importance of secondorder resonance through the simulation method with pseudo-spectral matrix-element (PSME) method[12], and Wang and Wu[13]also confirmed it based on the time domain analysis. However, the work on the second-order resonance has been only on surge or sway motion, or the tank oscillation in one direction. Practically, for most of the sloshing problems, the tank can have motions in all modes. For example, a ship usually has combined surge and sway motions. Based on the linear theory, the first-order overall motion is simply the superposition of the sway and surge motions, and there is no coupling between them. For the second-order problem, however, the simple superposition no longer applies and the generated coupling term should be taken into account in the simulation. Such a coupling term was missing in the 2-D second-order resonance analysis of Wu[9]for motion in one direction and is the focus of the 3-D second-order analysis for resonance in this paper. It is found that when the sumor difference excitation frequency of the surge and sway oscillations is equal to one of the natural frequencies, the second-order resonance occurs. It can also occur in other various conditions.

1. Mathematic analysis

We consider a 3-D rectangular tank of depth d, length 2l and width 2b undergoing horizontal oscillation. As shown in Fig.1, we adopt a right handed space fixed Cartesian coordinate system ox0y0z0, with the origin on the mean free surface and in the middle of the tank when it is stationary, and z0pointing upwards. The displacements of the tank in the x0and y0directions are s1( t) and s2( t) respectively. We assume that the fluid is inviscid and incompressible, and the flow is irrotational.

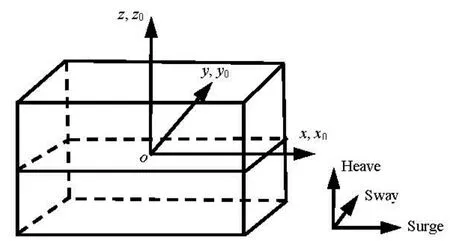
Fig.1 Cartesian coordinate systems ox0y0z0and oxyz

The fluid motion can then be described by a velocity potential φ which satisfies the Laplace equation

The elevation of the free surface can be written as z0=η(x0, y0, t ), or

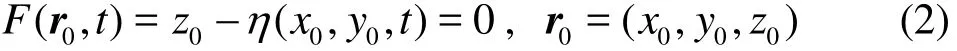
The kinematic condition on the free surface can then be written as

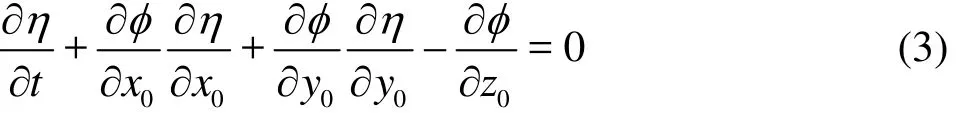
The dynamic condition on the free surface can be written as

where g is the acceleration due to gravity.

The tank bottom condition can be written as

According to Fig.1, we adopt the tank-fixed Cartesian coordinate system oxyz, which has the relation with ox0y0z0as

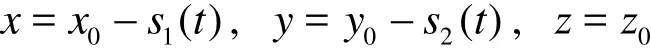
The kinematic condition and the dynamic condition on the free surface can be rewritten as

Assuming ε to be a small perturbation parameter using the ratio of the motion amplitude to the tank size, we can write

Substituting these two equations into Eqs.(9) and (10) and expanding the results from z=η to z=0 (the still-water level), we have

As the problem for φ(1)and η(1)is linear, we can adopt superposition to obtain the solution. If φ1(1)andare the linear solutions for the surge and sway motions respectively, thus the solution of φ(1)and η(1)can be written as

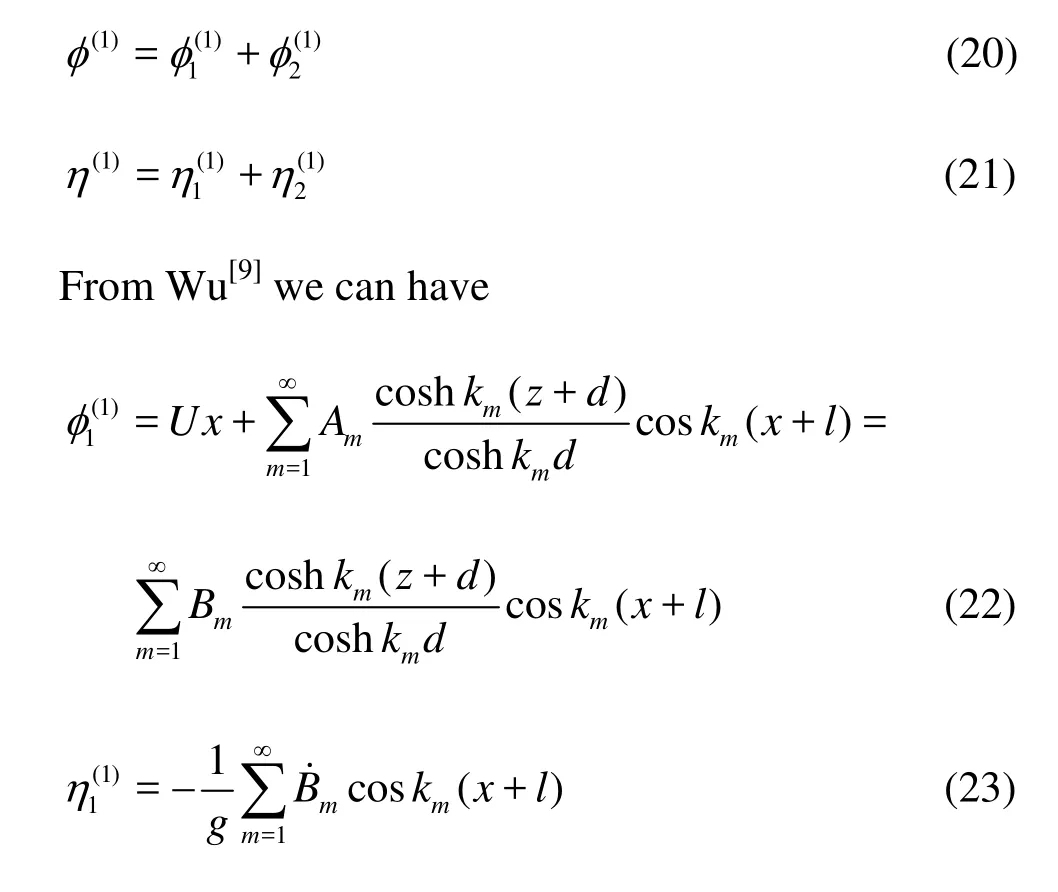
Apparently there are three parts in Eq.(27). Following Wu[9], we can write

We can know from Wu[9]that（2）1φ,（2）

2φ are the second-order potentials when the tank oscillates only in the x or y direction, respectively.is the solution due to the last part of Eq.(27), which is the coupling term between surge and sway, and is missing in the two-dimensional problem.

We assume that

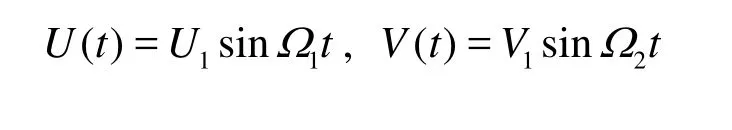
then we have

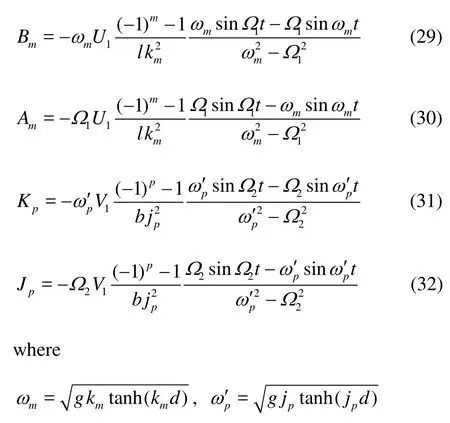
Substituting Eqs.(22)-(25) and Eqs.(29)-(32) into the last part of Eq.(27), we have

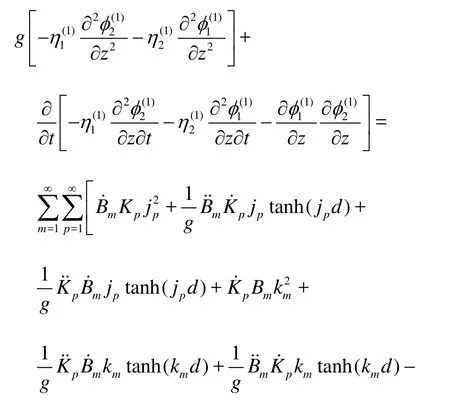
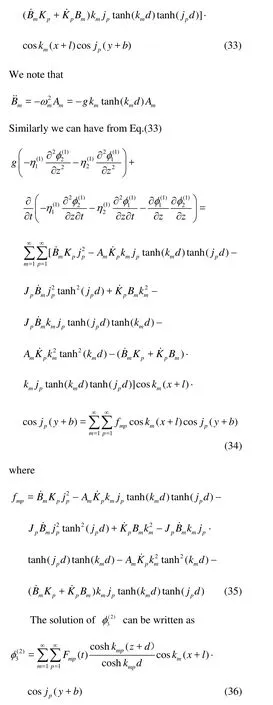
where

The initial condition of Fmp(t) can be obtained from Eq.(8), and with Eq.(16), we have

Based on the Laplace transform, the solution of Eq.(39) can be obtained as

Equation (41) shows that when fmp(τ) contains a periodic component of ωmp, the integration gives a term of t. Then fmp(t) tends to be infinite as t→∞, and the resonance will occur.

2. Numerical results and discussions

We consider the case of U( t)=U1sin Ω1t, V( t)=V1sin Ω2t. Further inspection of Eq.(34) shows that there are periodic terms with frequencies Ω2±Ω1,Ω2±ωm, ωp+ωm(m, p=1,3,...) in the equation.mω andare natural frequencies corresponding to the x and y directions, respectively, and from Wu[2]we can know that the natural frequencies in 3-D are ωmp(m, p=1,3,...).

Obviously, when m, p=2,4,..., Eq.(34) gives fmp=0, which means that the even modes only apply to the sway or surge motion , while odd modes apply to the coupling term. When one of the two motions corresponds to the odd modes while the other corresponds to the even modes such as the cases ωmp(m= 1,3,...,p =2,4,...)and ωmp(m=2,4,...,p =1,3,...), we can find that fmp=0 and no second-order resonance occurs based on Eq.(34). If any of these periodic terms mentioned above is equal to one of the odd modes of natural frequencies ωmp(m, p =1,3,...), the secondorder resonance will occur.

We take the odd mode m=1, p=1 for analysis, and according to Eq.(15), F11represents the amplitude of wave elevation for discussing the occurrence of second-order resonance. Figures 2(a) and 2(b) give F1= F11/(U1V1d/ g) against t1=tg/ d with l=d, b= 0.4l at Ω2+Ω1=ω11and Ω2-Ω1=ω11respectively. Both of the two cases correspond to the odd mode and the figures show that resonance is obvious.

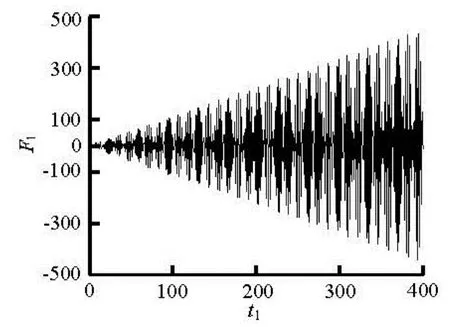
Fig.2(a) F1against t1at Ω2+Ω1=ω11, Ω2=0.5ω11, Ω1= 0.5ω11

Fig.2(b) F1against t1at Ω2-Ω1=ω11, Ω2=2ω11, Ω1= ω11

We next consider another case for second-order resonance. Figures 3(a) and 3(b) give results at Ω2± ω1=ω11, Ω1=0.5ω1respectively. The figures alsoshow that the wave elevation increases definitely as time progresses. Similarly, the resonance occurs at Ω1±＇=ω11, Ω2=＇ as shown in Figs.4(a) and 4(b). The above cases show that the second-order resonance can also occur when the excitation frequency of only one horizontal motion is equal to some certain value that is related to the natural frequencies.

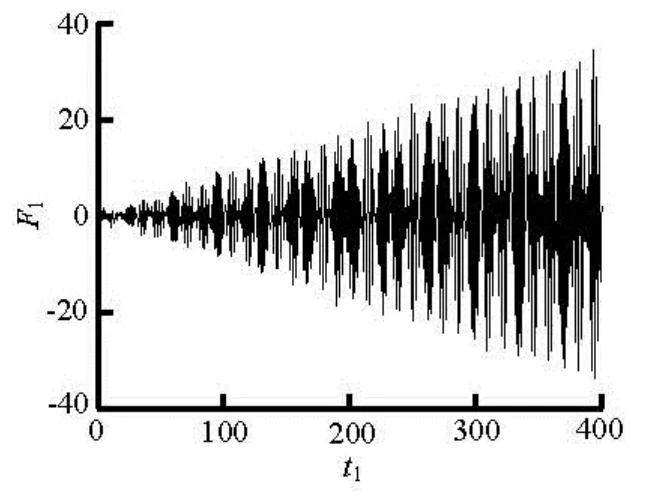
Fig.3(a) F1against t1at Ω2+ω1=ω11, Ω1=0.5ω1

Fig.3(b) F1against t1at Ω2-ω1=ω11, Ω1=0.5ω1

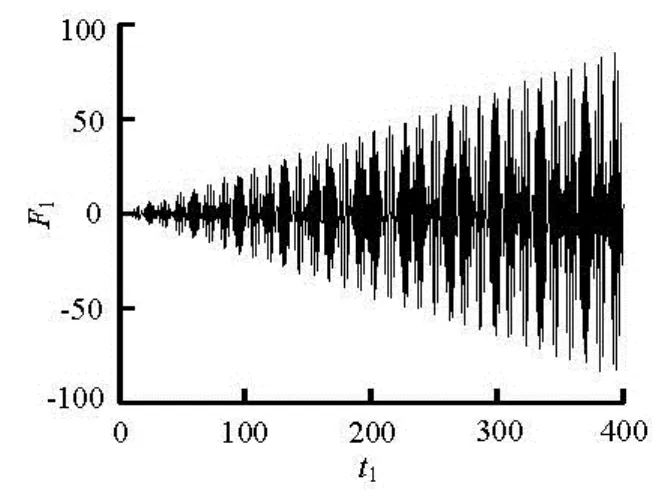
Fig.4(a) F1against t1at Ω1+=ω11, Ω2=

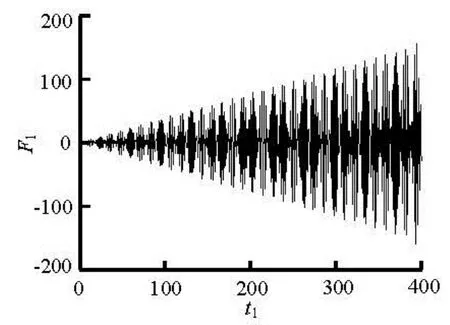
Fig.4(b) F1against t1at Ω1-＇=ω11, Ω2=

From Eq.(34), we find that the second-order resonance may occur when periodic term ω＇p+ωmsatisfies

However, Eq.(42) can only be satisfied for some particular value of d/2l and d/2b. We assume d=1 and = m1, and then Fig.5 shows the graph of function1ω against 1/2l (or 1/2b). From Fig.5, we find that Eq.(42) can only be satisfied when 1/2l≪0.1 or 1/ 2b≪0.1, that is to say, d/2l or d/2b are very small, which means that water is extremely shallow. However, under this condition, any possible secondorder resonance may have no practical interest because of the extremely small water depth.

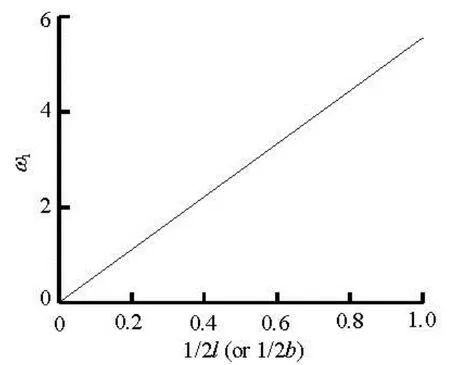
Fig.51ω against 1/2l (or 1/2b)

3. Conclusions

The problem of 3-D second-order resonance of sloshing in a tank has been analyzed, and the coupling term is found in the discussion of combined surge and sway motions. The importance of the second-order solution has already pointed out in the work of Wang and Wu[14]. In 2-D condition the second-order resonance occurs when the sum or difference frequency is equal to one of the natural frequencies of an even mode. For the 3-D condition, the coupling term between surge and sway plays an important part in the second-order resonance when there are excitations in surge and sway motions respectively. The secondorder resonance can occur when the sum or the difference of the two excitation frequencies of the surge and sway motions is equal to one of the natural frequencies of an odd mode. Another condition shows that when the sum or the difference frequency of one of the excitation frequencies and one of the natural frequencies is equal to another natural frequency, the second-order resonance also occurs.

It should be noted that the second-order resonance is promotional to the square of the excitation amplitude. Its importance will take much longer time to develop. Wu et al.[15]proved it is possible that the viscous effect on sloshing already becomes significantbefore its effect is obvious. This suggests that it may be more likely to happen for less viscous liquid at larger amplitude excitation. The present work can be further extended to sloshing of liquid with varying density along the depth.

[1] FALTINSEN O. M. A numerical non-linear method for sloshing in tanks with two dimensional flow[J].Jour-nal of Ship Research,1978, 18(4): 224-241.

[2] WU G. X., MA Q. W. and EATOCK TAYLOR R. Numerical simulation of sloshing waves in a 3D tank based on a finite element method[J].Applied OceanResearch,1998, 20(6): 337-355.

[3] WANG C. Z., KHOO B. C. Finite element analysis of two-dimensional nonlinear sloshing problems in random excitation[J].Ocean Engineering,2005, 32(2): 107-133.

[4] HUANG Hao-cai, WANG Chi-zhong and LENG Jianxing. Fully nonlinear simulations of wave resonance by an array of cylinders in vertical motions[J].ChinaOcean Engineering,2013, 27(1): 87-98.

[5] FALTINSEN O. M., TIMOKHA A. N. An adaptive multimodal approach to nonlinear sloshing in a rectangular tank[J].Journal of Fluid Mechanics,2001, 432: 167-200.

[6] HU P., WU G. X. and MA Q. W. Numerical simulation of nonlinear wave radiation by a moving vertical cyli- nder[J].Ocean Engineering,2002, 29(14): 1733-1750.

[7] MA Q. W., WU G. X. and EATOCK TAYLOR R. Finite element simulation of fully nonlinear interaction between vertical cylinders and steep waves. Part 1: Methodology and numerical procedure[J].International Journal for Numerical Methods in Fluids,2001, 36(3): 265-285.

[8] MA Q. W., WU G. X. and EATOCK TAYLOR R. Finite element simulation of fully nonlinear interaction between vertical cylinders and steep waves. Part 2: Numerical results and validation[J].International Journal for Numerical Methods in Fluids,2001, 36(3): 287-308.

[9] WU G. X. Second-order resonance of sloshing in a tank[J].Ocean Engineering,2007, 34(17-18): 2345- 2349.

[10] WANG C. Z., WU G. X. and KHOO B. C. Fully nonlinear simulation of resonant motion of liquid confined between floating structures[J].Computers and Fluids,2011, 44(1): 89-101.

[11] CHERN M.-J., VAZIRI N. and BORTHWICK A. G. L. Fully non-linear simulation of second-order resonance in a three-dimensional tank using the PSME method[J].Applied Ocean Research,2012, 37: 22-32.

[12] CHERN M.-J., VAZIRI N. and SYAMSURI S. et al. Pseudospectral solution of three-dimensional nonlinear sloshing in a shallow water rectangular tank[J].Journalof Fluids and Structures,2012, 35: 160-184.

[13] WANG C. Z., WU G. X. Time domain analysis of second-order wave diffraction by an array of vertical cylinders[J].Journal of Fluids and Structures,2007, 23(4): 605-631.

[14] WANG C. Z., WU G. X. Analysis of second-order resonance in wave interactions with floating bodies[J].Ocean Engineering,2008, 35(8-9): 717-726.

[15] WU G. X., EATOCK TAYLOR R. and GREAVES D. M. Viscous effect on the transient free surface flow in a two dimensional tank[J].Journal of Engineering Mathematics,2001, 40(1): 77-90.

10.1016/S1001-6058(14)60034-2

* Project supported by the National Science Foundation of China (Grant No. 51079082).

Biography: ZHANG Hong-sheng (1967-), Male, Ph. D., Professor