Effect of compressive stress on the dispersion relation of the flexural–gravity waves in a two-layer fluid with a uniform current*
LU Dong-qiang (卢东强)
Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, China
Computational Marine Mechanics Laboratory, Department of Mechanical Engineering, University of California, Berkeley, CA 94720, USA, E-mail: dqlu@shu.edu.cn
Effect of compressive stress on the dispersion relation of the flexural–gravity waves in a two-layer fluid with a uniform current*
LU Dong-qiang (卢东强)
Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China
Shanghai Key Laboratory of Mechanics in Energy Engineering, Shanghai University, Shanghai 200072, China
Computational Marine Mechanics Laboratory, Department of Mechanical Engineering, University of California, Berkeley, CA 94720, USA, E-mail: dqlu@shu.edu.cn
(Received March 17, 2014, Revised March 28, 2014)
The explicitly analytical solution is derived for the dispersion relation of the flexural–gravity waves in a two-layer fluid with a uniform current. The upper fluid is covered by a thin plate with the presence of the elastic, compressive and inertial forces. The density of each of the two immiscible layers is constant. The fluids of finite depth are assumed to be inviscid and incompressible and the motion be irrotational. A linear system is established within the framework of potential theory. A new representation for the dispersion relation of flexural–gravity waves in a two-layer fluid is derived. The critical value for the compressive force is analytically determined. The dispersion relation for the capillary–gravity with an inertial surface in a two-layer fluid can be obtained in parallel. Some known dispersion relations can be recovered from the present solution.
Hydroelasticity, compressive force, current, two-layer fluid
The ice sheet in the polar region and the pontoontype very large floating structure (VLFS) floating on the ocean are conventionally model as a thin elastic plate. It is assumed that there is no cavitations between the plate and the fluid, and the draft of the plate is negligible. For the plate deflection, the elastic and inertial forces are usually included. In 1987, Schulkes et al.[1]took account of three effects: (1) compressive stress in the plane of the plate, (2) uniform flow in the underlying water, (3) two-layer stratification of the underlying water. Recently, Sturova[2]studied the radiation (surge, sway and heave) of the flexural–gravity waves by a submerged sphere advancing in a homogenous fluid covered by a thin layer of elastic plate with lateral stress. Mohanty et al.[3]investigated the combined effect of current and compressive force on time-dependent flexural–gravity wave in both the cases of single and two-layer fluids for two-dimensional cases. In this Letter, the explicitly analytical expression is derived for the dispersion relation of the flexural–gravity waves with the combined effects of the compressive stress in the plate and the uniform current in a two-layer fluid. The capillary–gravity waves on an inertial surface can be seen as a special case of the present formulation.
Cartesian coordinates oxyz are taken and the z axis points vertically upward. The upper surface, the undisturbed interface and the flat bottom coincide with z=h1, z=0 and z=-h2, respectively. The two fluids are assumed to be inviscid and incompressible and the motion be irrotational. The uniform currents in the upper and lower layers are the same. The governing equation is

where Φm(x, y, z, t )is the velocity potential for the perturbed flow in the upper (m=1) and lower (m= 2) fluids.
It is assumed that the wave amplitudes generated are small in comparison with the wavelengths. So the linearized boundary conditions will be applied on the undisturbed upper surface and lower interface. Denote the densities of the upper and lower fluids by1ρ and ρ2with ρ1<ρ2, respectively. Let U be the speed of the current, and g the gravitational acceleration. Let E,eρ, d, and ν be Young’s modulus, the density, the thickness, and Poisson’s ratio of the plate, respectively. The boundary conditions on the upper surface (z=h1) are given by

where ζ1(x, y, t) and ζ2(x, y, t) are the upper surface and interfacial elevations with respect to z=h1and z=0, respectively, D=Ed3/[12(1-ν2)] is the flexural rigidity of the plate, Q is related to the lateral stress of the plate (with compression at Q>0 and stretch at Q<0)[2], and =eMρd. Equations (2) and (4) imply that fluids particles once on the surface or interface will always remain there. Equation (3) indicates the balance among hydrodynamic pressure of the fluids, the elastic, compressive, and inertial forces of the plate. Equations (5) and (6) represent the continuity of the normal velocity and the pressure on the interface, respectively.
The boundary condition at the flat bottom is

We assume that the solution of Eqs. (1)-(7) takes the form of
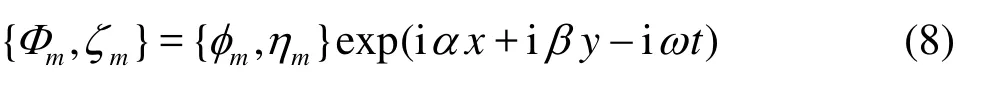
where α and β are the wave numbers in the x and y directions, and ω is the frequency. According to Eqs. (1) and (7), we have
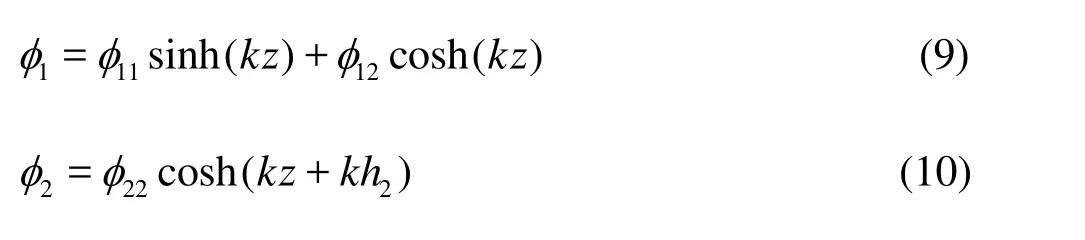
where φ11, φ12and φ22are undetermined functions, and k=. Substituting Eqs. (9) and (10) into Eqs. (2)-(6), we have a set of five linear equations for five unknown functions 1η, 2η, φ11, φ12, and φ22. The necessary condition for the existence of solution is that the determinant of the coefficients of the unknown functions is zero, which can be expressed by
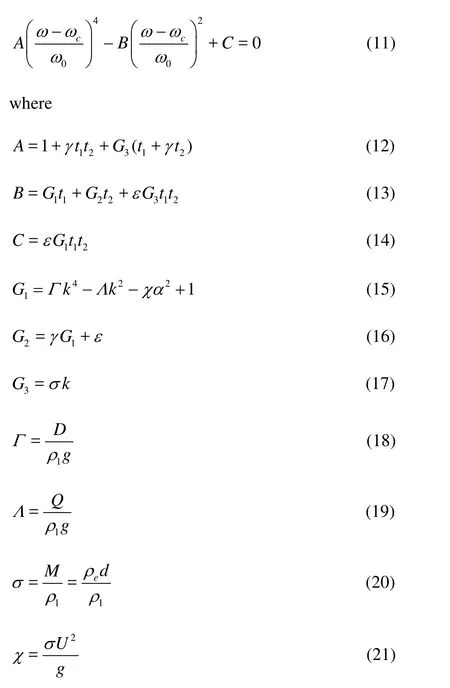
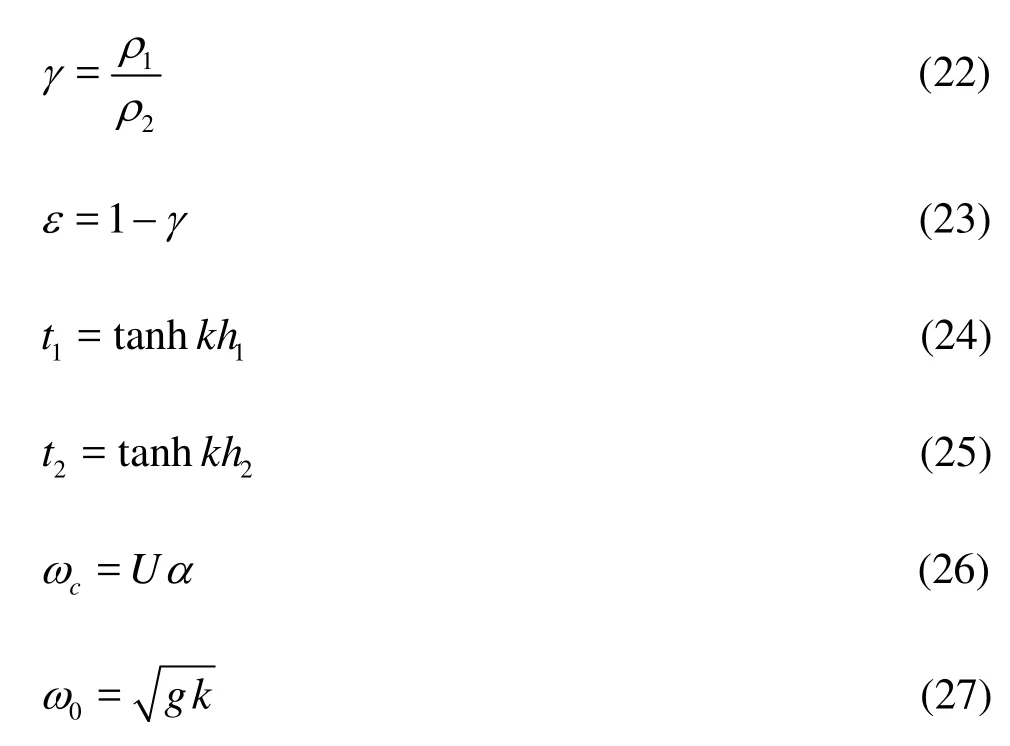
The explicitly analytical solution for Eq. (11) is readily given by
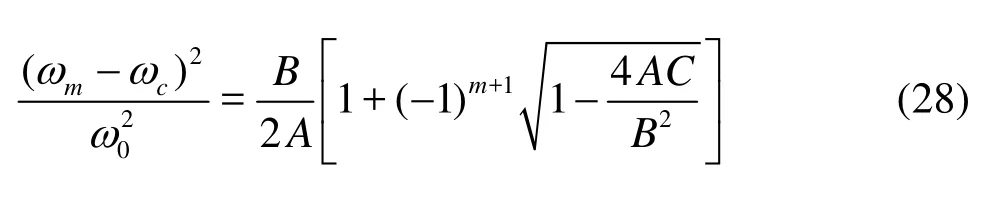

The dispersion relation for the flexural–gravity waves in a single fluid without a current was derived by Schulkes et al.[1]as

For a single fluid, one can see that as24= Λ-Γ0 namely

we have G1=0 and ω=0. Thus the wave propagation is possible if and only if Q<Q0. Therefore Q0is referred to as a critical value for Q in a single-layer fluid[1]. To study the effect of uniform current, we consider a two-dimensional case and then α2=k2. For the problem considered here, one can see that as
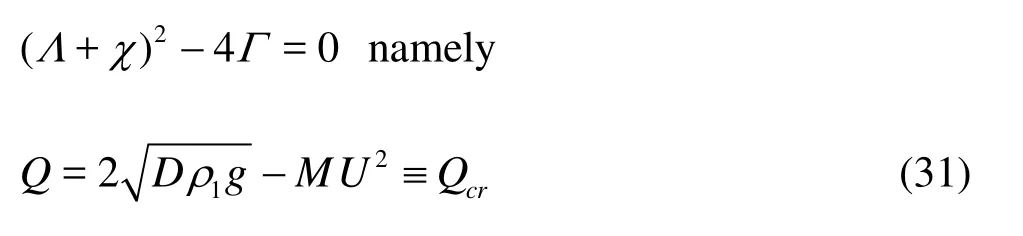
we have G1=0 and ω2=ωc. Therefore we can conclude that the Qcris the critical value for the compressive force with the effect of a uniform current.
[1] SCHULKES R., HOSKING R. and SNEYD A. Waves due to a steadily moving source on a floating ice plate. Part 2[J].Journal of Fluid Mechanics,1987, 180: 297-318.
[2] STUROVA I. V. Unsteady three-dimensional sources in deep water with an elastic cover and their applications [J].Journal of Fluid Mechanics,2013, 730: 392- 418.
[3] MOHANTY S. K., MONDAL R. and SAHOO T. Time dependent flexural gravity waves in the presence of current[J].Journal of Fluids and Structures,2014, 45: 28-49.
[4] LU Dong-qiang, SUN Cui-zhi. Transient flexural- and capillary-gravity waves due to disturbances in two-layer density-stratified fluid[J].Journal of Hydrodynamics,2013, 25(3): 339-347.
[5] YEUNG R. W., NGUYEN T. C. Waves generated by a moving sources in a two-layer ocean of finite depth[J].Journal of Engineering Mathematics,1999, 35(1-2): 85-107.
10.1016/S1001-6058(14)60037-8
* Project supported by the National Basic Research Program of China (973 Program, Grant No. 2014CB046203), the National Natural Science Foundation of China under (Grant No. 11072140), the Shanghai Program for Innovative Research Team in Universities.
Biography: LU Dong-qiang (1972- ), Male, Ph. D., Professor
- 水动力学研究与进展 B辑的其它文章
- Numerical prediction of 3-D periodic flow unsteadiness in a centrifugal pump under part-load condition*
- Coupled hydroelastic vibrations of an elliptical cylindrical tank with an elastic bottom*
- Experimental investigations of transient pressure variations in a high head model Francis turbine during start-up and shutdown*
- Improved conservative level set method for free surface flow simulation*
- Capillary effect on the sloshing of a fluid in a rectangular tank submitted to sinusoidal vertical dynamical excitation*
- Comprehensive analysis on the sediment siltation in the upper reach of the deepwater navigation channel in the Yangtze Estuary*

