关于平面解析系统的拟齐次分解
陈秀红,黄土森
(浙江理工大学理学院,杭州310018)
关于平面解析系统的拟齐次分解
陈秀红,黄土森
(浙江理工大学理学院,杭州310018)
通过解析函数的拟齐次分解与牛顿图,研究了平面解析系统的拟齐次分解问题。给出了拟齐次向量场空间的维数及平面解析系统的拟齐次分解定理,并用实例给出平面多项式系统拟齐次分解的具体算法。这些结果推广了平面解析系统的拟齐次分解中的有关结论,对研究平面高次奇点性态具有参考价值。
拟齐次多项式;牛顿图;拟齐次多项式向量场;拟齐次分解
0 引 言
在许多应用学科中经常需要研究非线性常微分方程。平面系统

的定性理论主要是根据方程本身研究相平面中轨线的拓扑结构或定性结构[1-2]。因为在系统的常点附近的轨线结构是平凡的,即可平行化的,所以研究平面系统的拓扑结构或定性结构的难点是研究奇点的局部轨线结构。现在通常把在奇点附近是否可以定义Poincaré返回映射的问题称为单值性问题,且这个问题一直是研究奇点局部轨线结构的经典问题。如果在奇点附近可以定义Poincaré返回映射,则称这样的奇点为单值奇点,并且对解析系统(即系统(1)中的X(x,y)与Y(x,y)均为解析函数)而言,这样的奇点只能是中心或焦点[3]。一旦确定奇点是单值的,则另外一个经典的问题是寻找条件以决定该单值奇点到底是中心还是焦点,即确定围绕单值奇点的所有轨线何时都是封闭的(至少在奇点的某个邻域如此)。这个问题称为Poincaré中心-焦点问题或稳定性问题[4]。
当奇点的线性化矩阵不恒等于零时,奇点的拓扑结构基本上已经得到解决[3]。当奇点的线性化矩阵恒等于零(这样的奇点通常称为退化奇点)时,奇点的拓扑结构远未解决[5]。目前国内外文献中研究这类问题的有效方法之一是使用blow-up技巧,即先对式(1)中X(x,y)与Y(x,y)在奇点进行齐次分解,然后作一系列的齐次blow-up变量变换,以便最终把奇点分解成为初等奇点(即系统(1)在奇点的线性化矩阵至少有一个特征值非零),然后再研究其拓扑结构或定性结构。Dumortier[6]证明了任何平面解析系统,更一般地,对于满足Lojasiewicz不等式的系统,总可以经过有限多次齐次blow-up变量变换,把退化奇点分解成为初等奇点,并由此研究奇点的拓扑结构或定性结构。然而,当系统的奇点的亚次数(即式(1)中X(x,y)与Y(x,y)在奇点Taylor展开式中的最低次数的最小值)比较大时,需要经过多次的blow-up变量变换,计算过程十分冗长。为了简化计算,Algaba等[4-5,7]利用牛顿图先对X(x,y)与Y(x,y)进行拟齐次分解,然后再做拟齐次blow-up变量变换,以便最终把奇点分解成为初等奇点。另外,在平面系统的可积性的分析中研究系统的拟齐次分解也是有意义的[5]。因此,在平面定性分析中拟齐次性的研究虽然在理论上与计算上类似于齐次性,但从动力学上来讲更有研究意义。
杜飞飞等[8]主要研究了牛顿图与拟齐次多项式的基本性质,并给出拟齐次多项式系统单值奇点是否是中心或者是焦点的充要条件;García等[9]研究了拟齐次多项式微分系统,并给出次数分别为2与3的所有拟齐次向量场的算法。本文通过解析函数的拟齐次分解与牛顿图,研究平面解析系统的拟齐次分解问题,给出拟齐次向量场空间的维数及平面解析系统的拟齐次分解定理,并用实例给出平面多项式系统拟齐次分解的具体算法。这些结果推广了文献[2,8]中的相应结论,对研究平面高次奇点性态具有重要意义。
1 解析函数的拟齐次分解
定义1.1[5]设

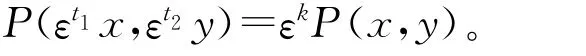
记t=(t1,t2)型k次拟齐次多项式构成的集合为。当t=(t1,t2)及k固定时,在通常的加法与数乘的意义下是一个线性空间。
引理1.2令t=(t1,t2)给定,则对任意的k∈Z+,存在唯一的一组k1,k2,k3和r∈Z+,使得k= k1t1+k2t2+k3t1t2+r,并满足k1<t2,k2<t1,0≤r<min{t1,t2}。
证明因为k与t1∈Z+,所以存在与s∈Z+使得k=+s,满足0≤s<t1,存在¯k2与r∈Z+使得s=+r,满足0≤r<min{t1,t2}。同理,存在与k1∈Z+使得=+k1,满足0≤k1<t2;存在与k2∈Z+使得=t1+k2,满足0≤k2<t1。于是

满足引理要求,其中k3=+。这证明了存在性。



从而

因为t1与t2互素,所以k1-=0,从而

因为0≤k2,<t1,所以k2-=0,故-=0。
为了讨论解析函数的拟齐次分解,引进记号

下面的引理在文献[4]中给出,但没有给出完整的证明。
引理1.3令t=(t1,t2)和k∈Z+给定,
(1)如果k∉It,则={0};
(2)如果k∈It并且 k=k1t1+k2t2+k3t1t2,则
证明由引理1.2知,存在唯一的一组k1,k2,k3和r∈Z+,使得

并满足k1<t2,k2<t1,0≤r<min{t1,t2}。
(1)因为k∉It,所以1≤r<min{t1,t2}。显然,零单项式0∈。如果单项式xmyn∈,由定义,mt1+nt2=k。因为对m,t2,存在唯一的,∈Z+使得m=+,且0≤<t2;对n,t1,存在唯一的∈Z+使得n=+,且0≤<t1。于是
这与1≤r<min{t1,t2}和分解的唯一性矛盾,故={0}。
(2)因为k=k1t1+k2t2+k3t1t2,又由上面的证明可知,如果单项式xmyn∈,则存在,使得m=+,n=+,且


故

于是

推论1.4固定的t=(t1,t2),如果k∈It并且k=k1t1+k2t2+k3t1t2,则

推论1.5令t=(t1,t2)给定,对任意单项式xmyn,取k=mt1+nt2,则xmyn∈。
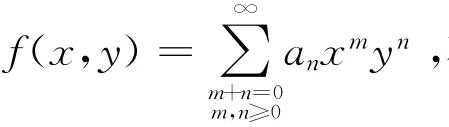
使得

并且这样的分解式是由t=(t1,t2)所唯一确定的。
证明由推论1.5及是线性空间立即得到。不过有可能对某些k使得(x,y)是零多项式。

2 解析向量场的拟齐次分解
给定平面解析系统

设(0,0)是(2)的奇点,即X(0,0)=Y(0,0)=0,所以在奇点的某个邻域内可以把X(x,y)和Y(x,y)分别展开成

解析系统(2)所对应的向量场记为F(x,y)=(X(x,y),Y(x,y))T,通常也表示为定义在连续可微函数类C1上的一个微分算子[5]

解析系统(2)的支撑集M是集合

M中的点(i,j)称为(2)的支撑点,向量(aij,bij)称为支撑点(i,j)的系数向量。系统(2)的牛顿多边形是集合(i,j∪)∈M((i,j)+)的凸包Γ,其中={(x,y)|x≥0,y≥0}。Γ的边界由两条射线和一条折线(这条折线可能退化为一点)组成,折线连通不在坐标轴上的射线称为系统(2)的牛顿图。牛顿图中的射线或折线上的线段,叫做牛顿图的边(折线上的线段也称为有界边或紧致边),它们的端点叫做牛顿图的顶点。显然,牛顿图中的顶点必为支撑集M中的点,反之不然。设l是系统(2)的牛顿图的一条有界边,则它的指数αl定义为l与纵坐标所夹的锐角的正切值。设l的两个端点分别为(i1,j1)和(i2,j2),因为l是有界边,所以可设i1<i2,j1>j2,于是αl=,其中,t1与t2是互素的正整数,数对t=(t1,t2)称为边l的类型。在上面一节的最后,我们注意到在研究解析系统奇点的性态时,只有那些对应于牛顿边的类型的拟齐次分解才是有意义的。为此先给出拟齐次多项式向量场的概念。
定义2.1[5]设

是一个多项式向量场(即P(x,y)与Q(x,y)都是多项式),称F是t=(t1,t2)型k次拟齐次多项式向量场,如果P(x,y)∈且Q(x,y)∈。
记t=(t1,t2)型k次拟齐次多项式向量场构成的集合为。当t=(t1,t2)及k固定时,在通常的加法与数乘的意义下是一个线性空间。为了把引理1.3推广到拟齐次向量场情形,首先注意到t=(t1,t2)型k次拟齐次多项式向量场是由一些t=(t1,t2)型k次拟齐次单项式向量场(xmyn,0)T与的线性组合而成的,进一步,如果xiyj-1∈,则xi-1yj∈并且(i-1)t1+(j-1)t2= k。下面的定理总结了上面的结果。
定理2.2对于解析系统(2),设t=(t1,t2)是它的一条牛顿边的类型,k∈Z+,
(1)如果k∉It,则={0}。
(2)如果k∈It并且k=k1t1+k2t2+k3t1t2,则=span{(xk1+1+t2(k3-j)yk2+t1j,0)T,(0,xk1+t2(k3-j)yk2+1+t1j)T|j=0,1,…,k3}。
推论2.3对于解析系统(2)的一条牛顿边的类型t=(t1,t2),如果k∈It并且k=k1t1+k2t2+k3t1t2,则dim=2(k3+1)。
定理2.4对于解析系统(2),设t=(t1,t2)是它的一条牛顿边的类型,则存在

或写成向量形式

证明可由定理2.2立即得到。
3 例 子
下面通过一些实例来验证本文所给出的方法是有效的。
例3.1考虑多项式系统

因为y=x0y2-1,x2+xy=x3-1y0+x2-1y1,从而M={(0,2),(3,0),(2,1)},所以该系统的牛顿图的有界边仅由一条连接(0,2)与(3,0)的线段组成,并且对应于该有界边的类型为t=(2,3)。于是式(4)可分解为

由于式(4)只有一条牛顿边,所以对分析奇点性态有意义的拟齐次分解也是唯一的。
例3.2考虑在文献[10]中出现的多项式系统

因为M={(4,3),(3,4),(2,5),(0,11),(11,0)},所以该系统的牛顿图的有三条有界边:连接(0,11)与(2,5)的线段l1,连接(2,5)与(4,3)的线段l2,连接(4,3)与(11,0)的线段l3,从而对分析奇点性态有意义的拟齐次分解有三种。下面分别根据牛顿边进行拟齐次分解。
对l1,因为其类型为t1=(3,1),于是式(5)可分解为

对l2,因为其类型为t2=(1,1),于是式(5)可分解为


[1]Andronov A A,Leontovich E A,Gordon I I,et al. Qualitative Theory of Second-Order Dynamic Systems[M].Jerusalem:Israel Program for Scientific Translations,1973.
[2]张芷芬,丁同仁,黄文灶,等.微分方程定性理论[M].北京:科学出版社,1985.
[3]Dumortier F,Llibre J,Artes JC.Qualitative Theory of Planar Differential Systems[M].Berlin:Springer-Verlag,2006.
[4]Algaba A,Freire E,Gamero E,et al.Monodromy,center-focus and integrability problems for quasi-homogeneous polynomial systems[J].Nonlinear Analysis,2010,71:1726-1736.
[5]Algaba A,García C,Reyes M.Characterization of a monodromic singular point of a planar vector field[J]. Nonlinear Analysis,2011,74(3/4):5402-5414.
[6]Dumortier F.Singularities of vector fields in the plane[J].Journal of Differential Equations,1977,23:53-106.
[7]Algaba A,Fuentes N,García C.Centers of quasi-homogeneous polynomial planar systems[J].Nonlinear A-nalysis:Real World Applications,2012,13:419-431.
[8]杜飞飞,黄土森.牛顿图的性质与拟齐次多项式系统的中心问题[J].浙江理工大学学报,2013,30(1):101-105.
[9]García B,Jaume Llibre J,Río JSP.Planar quasi-homogeneous polynomial differential systems and their integrability[J].Journal of Differential Equations,2013,255:3185-3204.
[10]Pelletier M.éclatements quasi homogeneous[J].Ann Fac Sci Toulouse,1995,4:879-937.
On the Quasi-Homogeneous Decomposition of PIanar AnaIytic System
CHEN Xiu-hong,HUANG Tu-sen
(School of Science,Zhejiang Sci-Tech University,Hangzhou 310018,China)
In this paper,the quasi-homogeneous decomposition of planar analytic system is studied through the quasi-homogeneous decomposition of the analytic function and Newton diagram.The dimension of the quasi-homogeneous vector field space and quasi-homogeneous decomposition theorem of the planar analytic system are given.Besides,the specific algorithm of quasi-homogeneous decomposition of planar polynomial system is given with examples.These results generalize relevant conclusions in associating references,and are helpful to study the qualitative properties of quasi-homogeneous decomposition of planar polynomial system and have reference value for studying higher-order singular point.
quasi-homogeneous polynomial;Newton diagram;quasi-homogeneous polynomial vector field;quasi-homogeneous decomposition
O175.14
A
(责任编辑:康 锋)
1673-3851(2014)05-0546-04
2014-01-08
国家自然科学基金项目(10871181,11101370)
陈秀红(1988-),女,山东菏泽人,硕士研究生,主要从事微分方程定性理论研究。

