一类三阶常微分方程的两点边值问题的正解

顿调霞，李永祥

(西北师范大学数学与统计学院，甘肃兰州730070)

1 预备知识

三阶微分方程有着深刻的力学与物理背景，可以利用它研究电磁波或者重力流等.近年来对各类三阶微分方程边值问题的研究十分活跃，多种非线性分析的工具与方法被应用于三阶微分方程边值问题的研究当中［1-14］，主要有基于微分不等式的方法、拓扑度方法、上下解方法与单调迭代技巧等.文献［1］在非线性项满足超线性或次线性增长的情况下，考察了问题

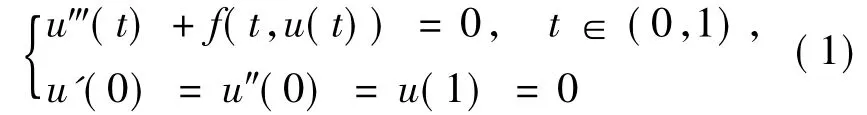
正解的存在性.文献［2］利用 Krasnoselskii不动点定理讨论了当非线性项f(t，u)可以在t=0，t=1及u=0处奇异时边值问题(1)正解的存在性与多解性.文献［3］应用上下解方法讨论了三阶两点边值问题

其中f:［0，1］×R→R连续，获得了一些解的存在性结果.受上述文献的启发，本文利用Krasnoselskii不动点定理，在用不等式条件描述非线性项增长的条件下，研究三阶常微分方程两点边值问题

正解的存在性，其中f:［0，1］×［0，∞)→［0，∞)连续.函数u*称为问题(3)的正解，如果u*是(3)式的解，并且u*(t) ＞0，0 ＜t≤1.

2 预备工作

设C［0，1］为定义在［0，1］上的连续函数全体按范数构成的 Banach 空间.

引理 1［4］对∀h∈C［0，1］，线性两点边值问题

引理2通过直接计算可得，由(6)式定义的函数G(t，s)具有下列性质

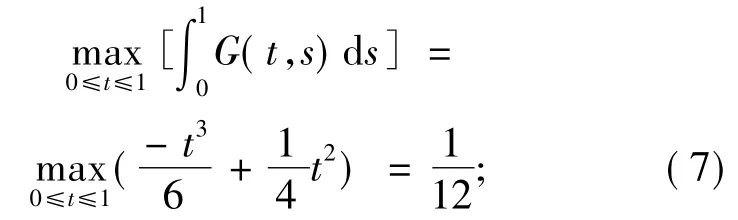
假设f:［0，1］×［0，∞ )→［0，∞ )连续，对∀u∈C［0，1］，定义

则F:C［0，1］→C+［0，1］连续.这里C+［0，1］={u∈C［0，1］|u(t)≥0，t∈［0，1］}为C［0，1］中的正元锥.

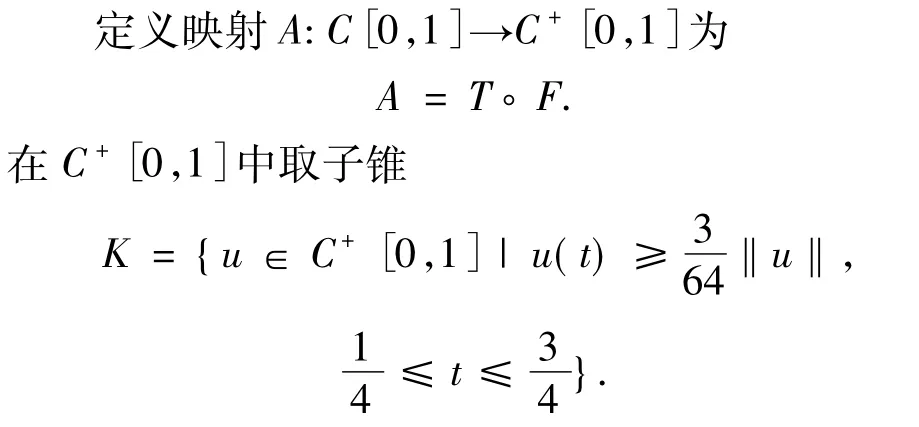
引理 3设f:［0，1］×［0，∞)→［0，∞)连续，则A(C［0，1］)⊂K且A:K→K全连续.

证明设u∈C［0，1］，对，根据(8)式有

因此Au∈K，从而A(C［0，1］)⊂K，A的全连续性可由Arzela-Ascoli定理推出.证毕.

于是由算子T的定义，边值问题(3)的正解等价于A在锥K中的不动点.

本文的主要工具是下面的锥拉伸与锥压缩型的Krasnoselskii不动点定理.

引理4［7］设E为Banach空间，K是E中的一个闭凸锥，Ω1、Ω2都是K中的有界子集满足θ∈Ω1，¯Ω1⊂Ω2，T:K∩(¯Ω2Ω1)→K为全连续映射，若下列条件之一成立:

1) ‖Tu‖≤‖u‖，∀u∈K∩∂Ω1，‖Tu‖≥‖u‖，∀u∈K∩∂Ω2；

2) ‖Tu‖≥‖u‖，∀u∈K∩∂Ω1，‖Tu‖≤‖u‖，∀u∈K∩∂Ω2.则T在K∩(¯Ω2Ω1)中至少有一个不动点.

3 主要结果

定理 1设f:［0，1］×［0，∞)→［0，∞)连续，若下列条件之一成立:

(H1)1) ∃δ＞0，使得当x∈Kδ时，f(t，x)≤12x；

2)及H＞0，使得当x≥H时，f(t，x)≥mx，

(H2)1)及 δ＞0，使得当x∈Kδ时，f(t，x)≥mx；

2) ∃H＞0，使得当x≥H时，f(t，x)≤12x，则边值问题(3)至少存在一个正解，其中Kδ=K∩¯B(0，δ).

证明假设(H1)成立，取0＜r＜R＜+∞，令

则 θ∈Ω1且 ¯Ω1⊂Ω2.

首先证明，当r适当小时，有‖Au‖≤‖u‖，u∈∂Ω1∩K.

取r∈(0，δ)，其中 δ为条件(H1)的 1)中的常数.从而，当u∈∂Ω1∩K时，有0＜u(s)≤‖u‖ =r＜δ，∀s∈(0，1)，由条件 (H1)的 1)知:对∀s∈(0，1)，f(s，u(s))≤12u(s)≤12‖u‖，所以

［1］蒋达清.三阶非线性微分方程正解的存在性［J］.东北师范大学学报:自然科学版，1996，28(4):6-10.

［2］姚庆六.一类奇异三阶微分方程的两点边值问题的正解［J］.南开大学学报:自然科学版，2011，44(1):92-96.

［3］Yao Q，Feng Y.The existence of solutions for a third order two-point boundary value problem［J］.Appl Math Lett，2002，15:227-232.

［4］Jackon L K.Existence and uniqueness of solutions of boundary value problems for third order differential equations［J］.J Diff Eqns，1973，13:432-437.

［5］Cabada A.The method of lower and upper solutions for second，third，fourth and higher order boundary value problems［J］.J Math Anal Appl，1994，185:302-320.

［6］姚庆六.三阶常微分方程的某些非线性特征值问题的正解［J］.数学物理学报，2003，A23(5):513-519.

［7］Li S.Positive solutions of nonlinear singular third-order two-point boundary value problem［J］.J Math Anal Appl，2006，323:413-425.

［8］姚庆六.一类非线性三阶两点边值问题的单调迭代方法［J］.云南大学学报:自然科学版，2011，33(1):1-5.

［9］张立新.三阶边值问题的3个正解的存在性［J］.四川师范大学学报:自然科学版，2011，34(4):466-470.

［10］陈丽，胡良根，马晓丹.奇异三阶微分方程特征值问题正解的存在性［J］.应用泛函分析学报，2012，14(4):377-387.

［11］冯育强，刘三阳.一类非线性三阶边值问题的可解性［J］.工程数学学报，2007，24(3):543-546.

［12］姚庆六.一类非线性三阶三点边值问题的解和正解［J］.数学杂志，2007，27(6):704-708.

［13］孙建平，彭俊国，郭丽君.非线性三阶三点边值问题的正解［J］.兰州理工大学学报:自然科学版，2009，35(1):139-142.

［14］赵薇.奇异三阶微分方程m点边值问题的正解［J］.四川师范大学学报:自然科学版，2013，36(2):252-257.

［15］李永祥.二阶非线性常微分方程的正周期解［J］.数学学报，2002，45:481-488.

［16］郭大钧.非线性泛函分析［M］.济南:山东科学技术出版社，1985.