一类中立型捕食者-食饵系统的正周期解
李建东
(吕梁学院 数学系,山西 吕梁 033000)
LI Jiandong
(Department of Mathematics,Lüliang University,Lüliang 033000,China)
一类中立型捕食者-食饵系统的正周期解
李建东
(吕梁学院 数学系,山西 吕梁 033000)
捕食者-食饵是种群生态学中一类重要的模型,考虑了一类带有Watt型功能反应的中立型捕食者-食饵系统,利用重合度理论中的延拓定理和一些数学分析方法,得到该系统正周期解的存在性,并推广了有关结果.
捕食-食饵系统;中立型;延拓定理
1 引言及预备知识
捕食者-食饵是一类重要的种群模型,其定性研究受到了很多国内外专家和学者的关注,并产生了许多具有很强实际背景的研究课题.
根据生物实验以及捕食者与食饵的内在变化规律,国内外许多学者研究了具有不同功能反应的捕食者-食饵系统,如Monod型功能反应[1]、Holling型功能反应[2]、Bedington型功能反应[3]等.
文献[4]建立了具有Watt型功能反应的捕食者-食饵系统:
(1)
由于Watt型功能反应能够合理地刻画一些捕食者与食饵之间的关系,受到许多生物数学专家的重视,并做了一些很好的研究工作[5-7].
2001年,Fan 和Wang[8]研究了下列比率依赖型捕食者-食饵系统:
(2)
的周期解与稳定性.
本文将利用延拓定理研究下列具有Watt型功能反应的中立型捕食者-食饵系统:
(3)
正周期解的存在性.

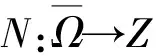
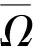
对于连续的正的ω-周期函数p(t), 定义:
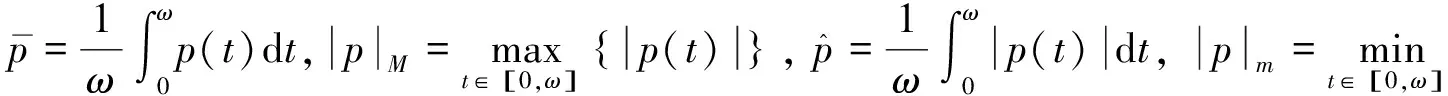
在系统(3)中,假设:
(H1)b,ρ,n∈(0,+);m∈(0,1);σ∈R;a∈C(R,R);c,d,f,k∈C(R,[0,+])是ω-周期函数;
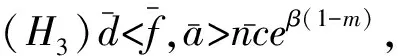
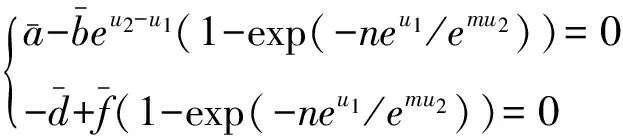
2 主要结果
定理1 若(H1)~(H4)成立,则系统(3)至少存在一个正ω-周期解.
证明令x(t)=eu1(t),y(t)=eu2(t),系统(3)可写为:
(4)
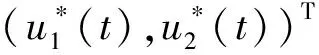
X={u=(u1(t),u2(t))T∈C1(R,R2):ui(t+ω)=ui(t),t∈R,i=1,2},
Z={u=(u1(t),u2(t))T∈C(R,R2):ui(t+ω)=ui(t),t∈R,i=1,2},
其中X的范数为|u|{|u1(t)|+|u2(t)|},Z的范数为‖u‖=|u|+|u′|.令L:X→Z为:
L(u1(t),u2(t))T=(u1′(t),u2′(t))T.
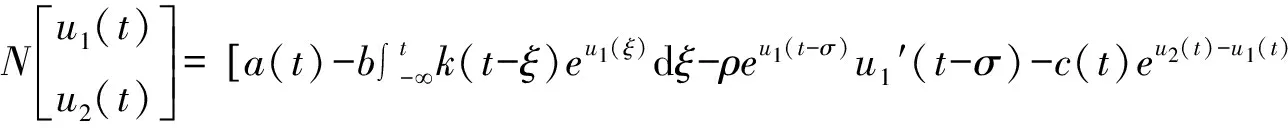
(1-exp(-neu1(t)/emu2(t)))-d(t)+f(t)(1-exp(-neu1(t)/emu2(t)))].

显然,KerL=ImP=R2,KerQ=ImL=Im(1-Q). 此外,dimKerL=codim ImL=2,因此L为一个指标为零的Fredholm算子.LP的逆KP:ImL→DomL∩KerP为:
另外,QN:X→Z为:
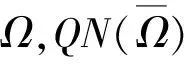
对于任意λ∈(0,1),考虑方程Lu=λNu,即:
(5)
若(u1(t),u2(t))T∈X是系统(5)的解,则:
(6)
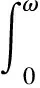
(7)
根据式(6),
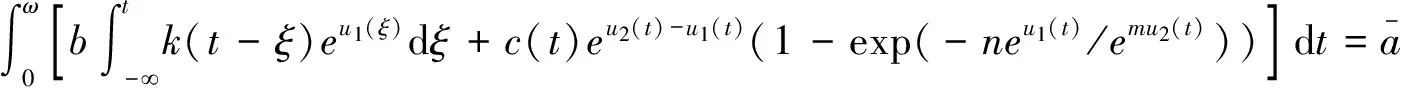
(8)
根据式(7),
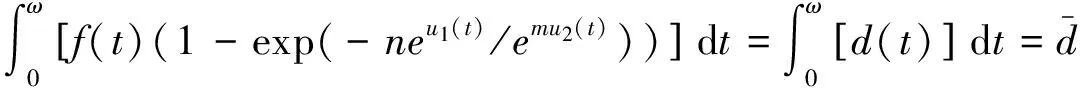
(9)
根据式(5)~(8)及条件(H1),
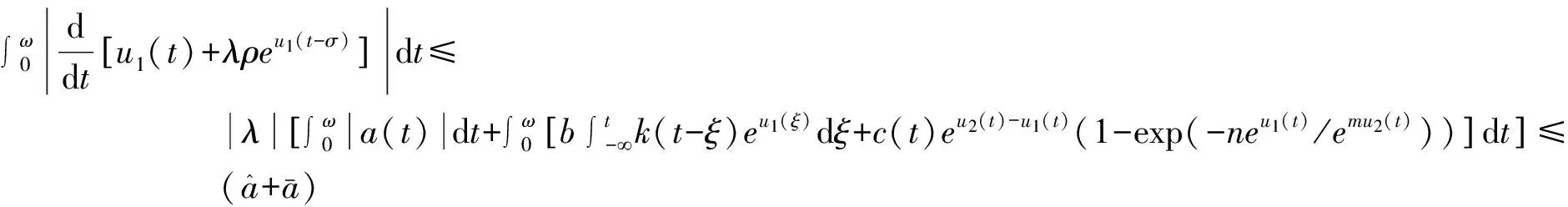
(10)
由式(6),

(11)
另外,
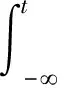
(12)
根据式(11)与式(12)得:
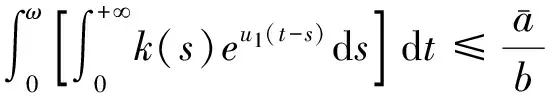
(13)
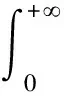
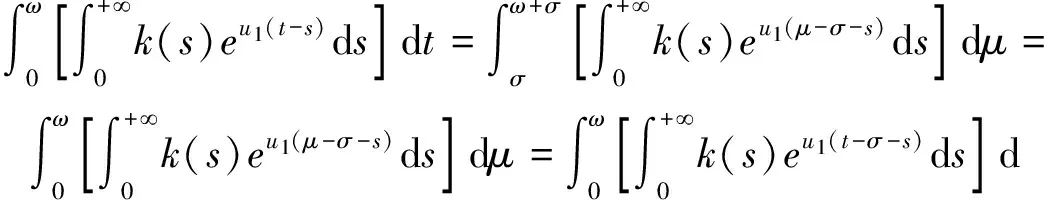
所以,
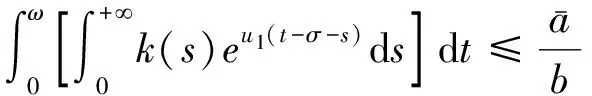
(14)
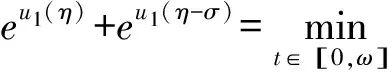
(15)
根据式(15)与条件(H1),
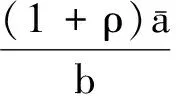
(16)
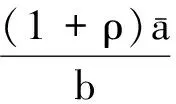
(17)
根据式(10),式(16)~(17),任意t∈[0,ω],
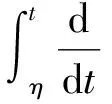
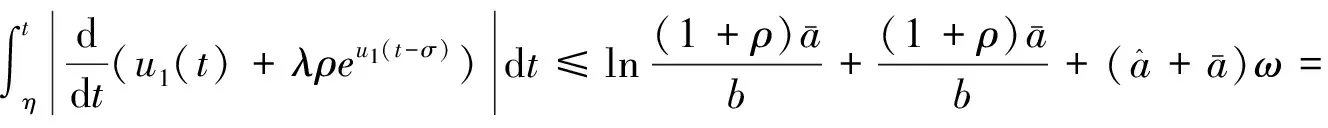
所以对任意t∈[0,ω],
u1(t)≤B.
(18)
根据式(5),式(8),式(18),
c(t)eu2(t)-u1(t)(1-exp(-neu1(t)/emu2(t)))|dt≤
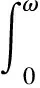

利用(H2),
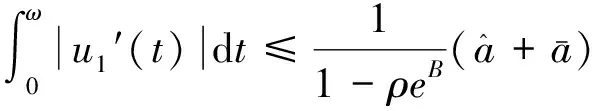
(19)
根据式(5)与式(9),
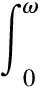
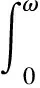
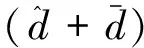
(20)
任意(u1(t),u2(t))T∈X,有ξi,ηi∈[0,ω],i=1,2使:

(21)
根据式(8),式(21)和条件(H3),
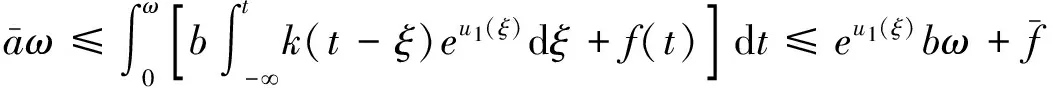
所以,
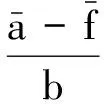
(22)
根据式(19),式(22),任意t∈[0,ω],
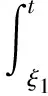
(23)
根据式(18),式(23),
(24)
利用条件(H3),
由于:
|u2′(t)|=|λ[-d(t)+f(t)(1-exp(-neu1(t)/emu2(t)))]|≤|d(t)|+|f(t)|≤|d|0+|f|0,
所以:
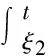
(25)
根据式(9),式(24)及条件(H3),
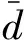
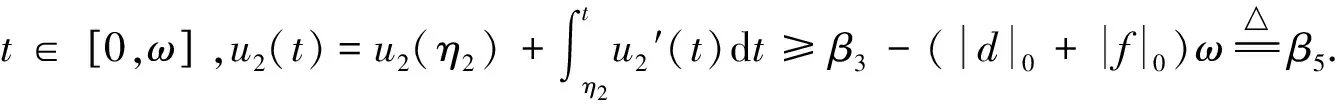
(26)
根据式(5),式(18),式(24)及式(26),
通过条件(H2),
(27)
因为|u2′(t)|≤|d|0+|f|0,所以:
(28)
根据式(24),式(26)~(28),
‖u‖=|u|+|u′|≤β2+β6+β7+β8.
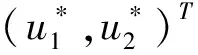
令β=β2+β6+β7+β8+β0.显然β与λ无关.令:Ω={(u1(t),u2(t))T∈X:‖(u1(t),u2(t))T‖<β}.
显然引理1中的条件(1)满足.当(u1(t),u2(t))T∈∂Ω∩KerL=∂Ω∩R2时,(u1(t),u2(t))T∈R2满足|u1|+|u2|=β.根据条件(H4),QN(u1,u2)T≠(0,0)T,即,引理1中的条件(2)满足.
令J=I:ImQ→KerL,(u1,u2)T→(u1,u2)T.记:
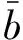
根据条件(H1), deg{JQN,Ω∩KerL,0}=
从而引理1中的条件(3)满足.因此系统(4)至少存在一个ω-周期解.即系统(3)至少存在一个正ω-周期解.
[1]Wang F,Zhang S,Chen L,et al.Bifurcation and complexity of Monod Type predator-prey system in a pulsed chemostat[J].Chaos,Solitons﹠Fractals,2006,27:447-58.
[2]Liu B,Teng Z,Chen L.Analysis of a predator-prey model with Holling Ⅱ funvtional response concerning impulsive control strategy[J].J Comput Appl Math,2006,193:347-362.
[3]Li Z,Wang W,Wang H.The dynamics of a Beddington-type system with impulsive control strategy[J].Chaos,Solitons﹠Fractaals,2006,29:1229-1239.
[4]Watt.A mathematical model for the effect of densities of attacked and attacking species on the number attacked[J].Can Entomol,1959,91:129-144.
[5]Lin X Q,Jiang Y L,Lin Y Z,et al.The dynamical complexity of an impulsive Watt-type prey-predator system[J].Chaos,Solitons﹠Fractals,2009,40:731-744.
[6]Wang W M,Wang X Q,Lin Y Z.Complicated dynamics of a predator-prey system with Watt-typt functional response and impulsive sontrol strategy[J].Chaos,Solitons﹠Fractals,2008,37:1427-1441.
[7]Lin X L,Jiang Y L,Wang X Q.Existence of periodic solution in predator-prey with Watt-type functional response and impulsive effeces[J].Nonlinear Analysis,2010,73:1684-1697.
[8]Fan M,Wang K.Periodicity in delayed ratio-dependent predator-prey system[J].J Math Anal Appl,2001,262:179-190.
[9]Gaines R E,Mawhin J L.Coincidence Degree and Non-linear Differential Equations[M].Berlin:Springer Press,1977.
责任编辑:时凌
ThePositivePeriodicSolutionsofaClassofNeutralPredator-preySystem
Predator-prey is a kind of important model in population ecology.In this paper, a class of neutral predator- prey system with Watt-type functional response is considered. Using the continuation theorem of coincidence degree theory and some mathematical analysis method, we obtain the existence of positive periodic solutions of this system and generalize the results in the existing literature.
predator-prey system;neutral;continuation theorem
2014-11-04.
李建东(1978- ),男,讲师,主要从事微分方程及其应用的研究.
O175.14
A
1008-8423(2014)04-0402-06
LI Jiandong
(Department of Mathematics,Lüliang University,Lüliang 033000,China)

