极坐标系下旋转体体积公式的推广

陈珍培

(浙江树人大学基础部,浙江杭州310015)

1 引 言

在定积分的几何应用中,有关旋转体体积的计算问题,一般都是在直角坐标系下进行讨论的,极坐标系下旋转体的体积计算问题,则很少提及. 文[1]，[2]给出了曲边扇形绕极轴旋转所得旋转体的体积计算公式， 但有关曲边扇形绕任意空间直线(过极点)旋转所得的旋转体体积问题,至今还没有文献进行论述.本文运用微积分的有关知识来解决这一问题.

2 球底圆锥壳及其体积

由于曲边扇形绕空间直线旋转所得旋转体的空间结构比较复杂,为此,先引入球底圆锥壳的定义及其体积的计算公式.

定义设C是半径为R的球面，C1，C2是以C的球心为顶点、半顶角分别为α和β的同轴圆锥面(其中β>α), 称由C，C1，C2围成的空间立体Ω为球底圆锥壳. 而R,α和β-α分别称为球底圆锥壳的斜高、半顶角和厚度角，C1，C2称为球底圆锥壳的内、外圆锥面.

结论1斜高为R、半顶角为α、厚度角为Δα的球底圆锥壳Ω的体积为

(1)

证显然, 球底圆锥壳体积为

结论2当球底圆锥壳的厚度角Δα→0时，其体积

(2)

证由(1)可得

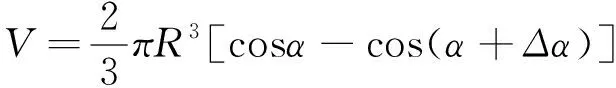
3 旋转体体积元素的构造

如图1,设O-xyz为空间坐标系，xOy坐标面上有一曲边扇形区域T，在极坐标系下表示为T={(r,θ)0≤r≤r(θ),α≤θ≤β}，旋转轴l经过原点且方向向量s=(m,n,p)为单位向量.在[α,β]上任意取一小区间[θ,θ+dθ](dθ>0)，得相应的小曲边扇形OMM1,它绕l旋转所得旋转体近似为球底圆锥壳，显然其斜高为OM=r(θ)，而半顶角φ及厚度角(显然为dφ)的计算如下：

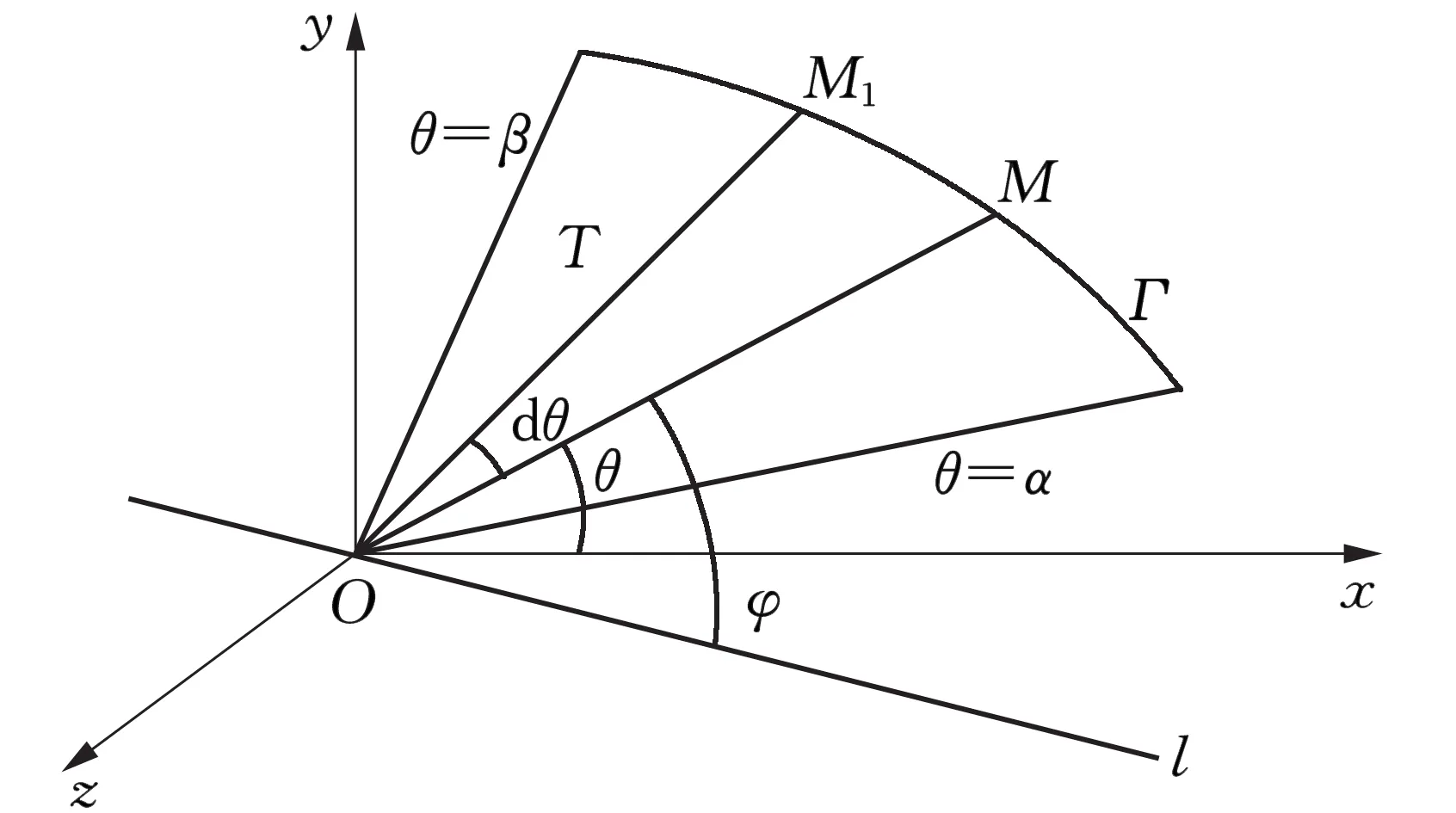
图1 旋转体体积元素构造示意图

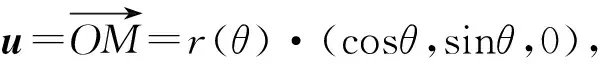
(3)

两边微分，得

-sinφdφ=-(msinθ-ncosθ)dθ，

所以

由(2)可得球底圆锥壳的体积(即旋转体体积元素)为

(4)

4 旋转体体积公式及证明

(5)

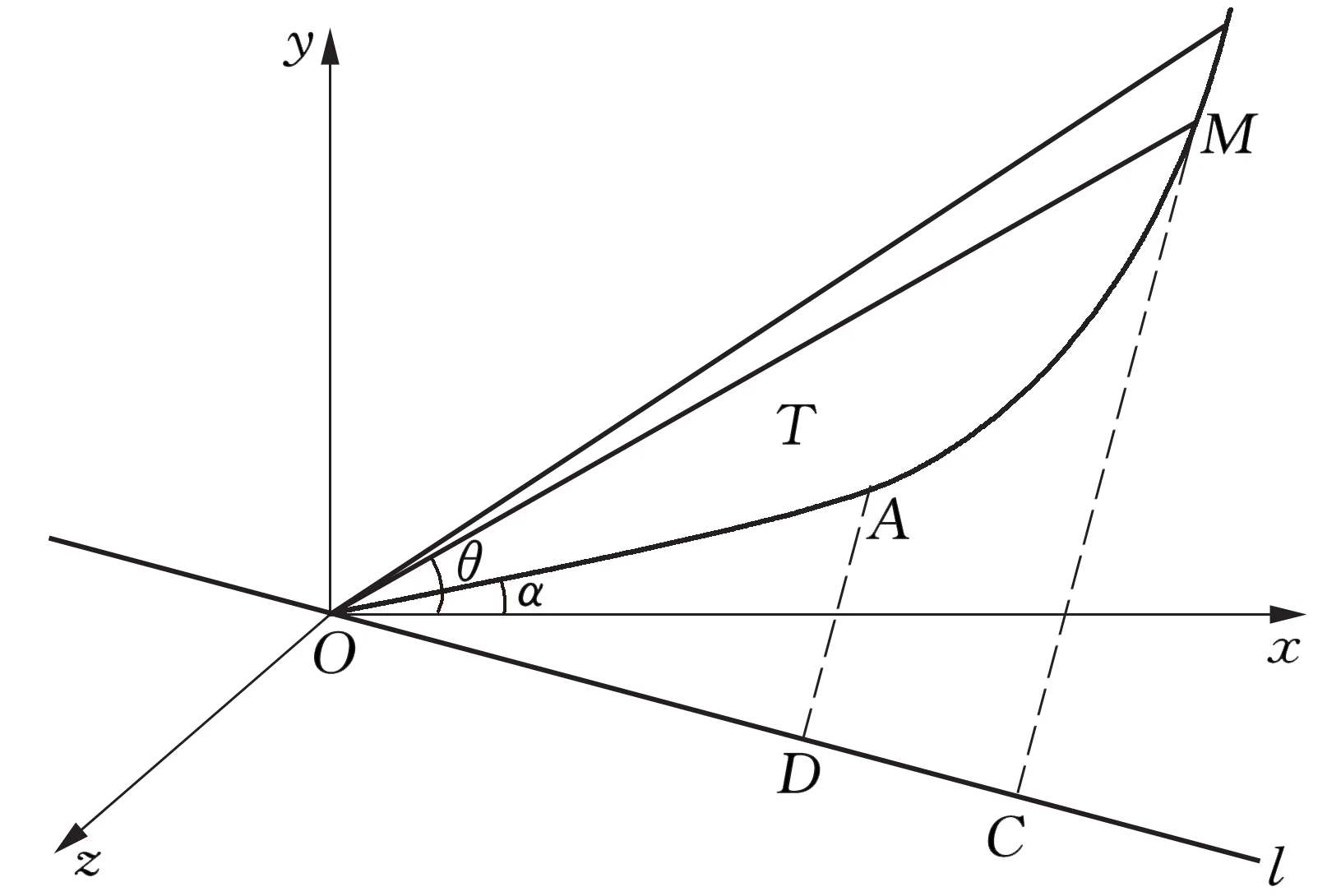
图2 旋转体体积公式推导示意图

注1 为使证明过程简洁,不妨先做以下假设:

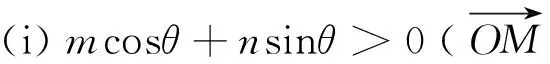
(ii) 随θ的增加,曲线上点的运动方向与s的夹角为锐角(证明中保证mx′+ny′+pz′>0)

(iii)m·sinθ-n·cosθ≥0 (能保证旋转体没有重复部分)

任意取θ∈[α,β],得曲边扇形AOM,过A，M分别作l的垂线，垂足为D，C, 见图2,记ΔOMC，ΔOAD及空间曲边四边形AMCD绕l所得旋转体的体积分别为V1,V2,V3.则

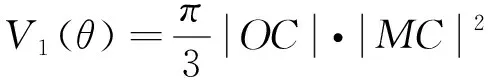
同理可得

由文[3]中的公式(1)可得当旋转轴过原点且方向向量为单位向量时，旋转体体积公式为

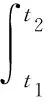
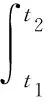
将x=r(θ)cosθ,y=r(θ)sinθ,z=0代入，得

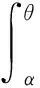
显然曲边扇形AOM绕l的旋转体体积为

V(θ)=V1(θ)-V2(θ)-V3(θ)，

所以

V′(θ)=V′1(θ)-V′2(θ)-V′3(θ).

而

V′1(θ) =πr2(θ)r′(θ)(mcosθ+nsinθ)[1-(mcosθ+nsinθ)2]

=πr2(θ)r′(θ)(mcosθ+nsinθ)[1-(mcosθ+nsinθ)2]

V′2(θ)=0,

V′3(θ) =πr2(θ)[1-(mcosθ+nsinθ)2]·[r′(θ)(mcosθ+nsinθ)+r(θ)(ncosθ-msinθ)]

=πr2(θ)r′(θ)(mcosθ+nsinθ)[1-(mcosθ+nsinθ)2]

+πr3(θ)(ncosθ-msinθ)][1-(mcosθ+nsinθ)2],

所以

从而体积元素为

所以旋转体体积

再考虑到体积非负，所以旋转体体积公式为

注2 (i) 若l的方向向量(m,n,p)不是单位向量，则体积公式变为

(6)

(ii) 当n=p=0时，此时旋转轴为x轴且取m=1,公式(5)简化为

此为文[1]，[2]的结论.

例1计算T={(r,θ)0≤r≤sin2θ,0≤θ≤π/4}绕l:x=y=z旋转所得旋转体的体积V.

解取l的单位方向向量

由n·cosθ-m·sinθ=cosθ-sinθ≥0知旋转体没有重叠部分,根据公式(5)得

5 性 质

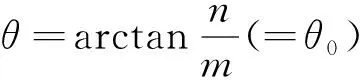
证在曲线r=r(θ)上任意取关于θ=θ0对称的两点M1(θ0-δ,r(θ0-δ)),M2(θ0+δ,r(θ0+δ)),设OM1,OM2绕l旋转所得的圆锥面分别为C1,C2,其斜高分别为r(θ0-δ),r(θ0+δ)，根据T的对称性，显然有r(θ0-δ)=r(θ0+δ).

再设C1,C2的半顶角分别为φ1,φ2，由(3)可得

所以

cosφ1-cosφ2=2m·sinθ0sinδ-2n·cosθ0sinδ

故φ1=φ2，从而两个圆锥面C1,C2的半顶角和斜高分别相等，即两个圆锥面重合，由取点的任意性可知T1和T2绕l所得的旋转体重合.

性质2设两根旋转轴l1和l2的方向向量分别为s1=(m,n,p1)和s2=(m,n,p2)，则xOy平面内的曲边扇形绕l1和l2所得的体积V1和V2之比为

证由公式(6)显然可得.

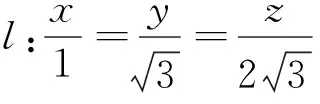
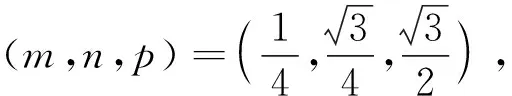
T1={(r,θ)0≤r≤R,0≤θ≤π/3}

和

T2={(r,θ)0≤r≤R,π/3≤θ≤π/2}，

根据性质(1),T2所得的旋转体包含在T1所得的旋转体中，所以只要求T1所得的旋转体体积即可，所以

[参 考 文 献]

[1] 邸双亮.曲边扇形绕极轴旋转体体积的新算法[J].高等数学研究,1995(1):27-29.

[2] 燕列雅,赵彦晖.极坐标系下旋转体体积元素的直接构造法[J].高等数学研究,2007,10(6):17-18.

[3] 王林芳,马雅琴.空间情形下旋转体体积的计算[J].数学的实践与认识,2006,36(5):304-307.