ρ－混合序列部分和之和乘积精确渐近性的一般形式

邹 广 玉

（长春工程学院 理学院，长春130012）

0 引言与主要结果

部分和之和乘积理论在破产理论记录值分布中应用广泛，对其极限性质的研究已取得许多结果.文献［1］得到了ρ－混合序列部分和之和乘积的渐近分布；文献［2－3］分别得到了相伴及α－混合序列部分和之和乘积的几乎处处中心极限定理等.精确渐近性［4－9］是近年发展起来的研究热点，但关于部分和之和乘积的精确渐近性却鲜有报道.本文讨论ρ－混合序列部分和之和乘积精确渐近性的一般形式.

定义1 设A和B是两个σ域，记Fba＝σ（Xt，a≤t≤b）.定义

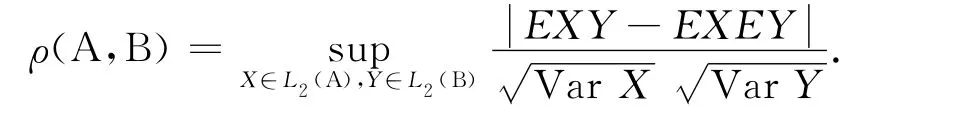
本文假设以下条件成立：

（H1）g（x）为［n0，∞）上具有非负导数g′（x）的可导的正函数，且满足g（x）↑∞，x→∞；

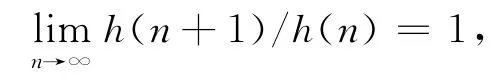
本文主要结果如下：

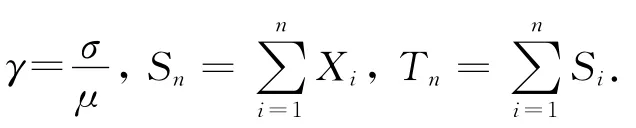
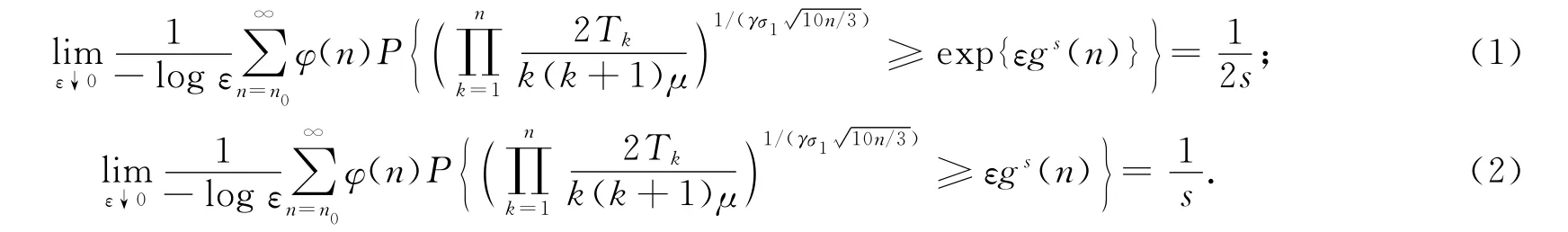
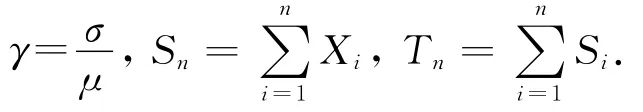
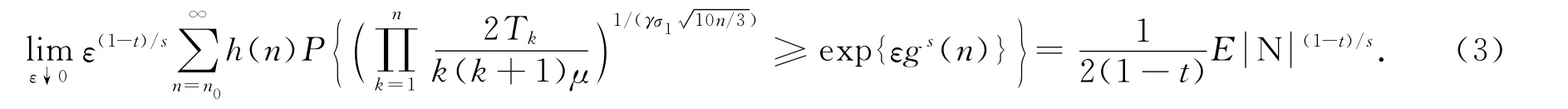
其中N表示标准正态随机变量.

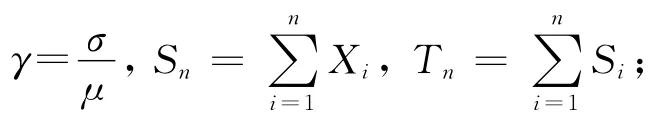
注2 满足假设条件（H1）～（H3）的g（x）有很多，可取g（x）＝xα，（log x）β，（loglog x）γ等，其中α＞0，β＞0，γ＞0为某些适当的参数.

1 引 理

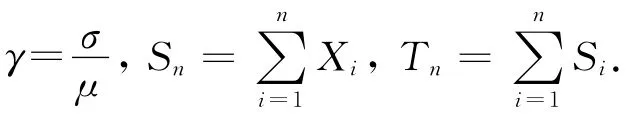
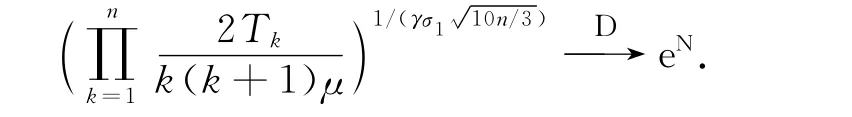
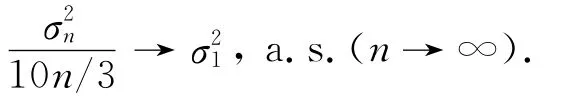
证明：注意到b1，n～log n，由文献［1］中引理2.4易证结论成立.

2 定理的证明

2.1 定理1的证明

令b（ε）＝［g－1（ε－r）］，其中g－1（x）为g（x）的反函数，r＞1／s.

命题1 在定理1的条件下，有：

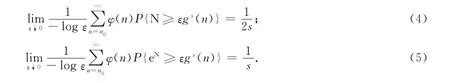
证明：只证明式（4）成立.式（5）的证明类似.考虑积分和级数之间的关系.如果φ（y）单调非增，则φ（y）P｛N≥εgs（y）｝也单调非增，从而有

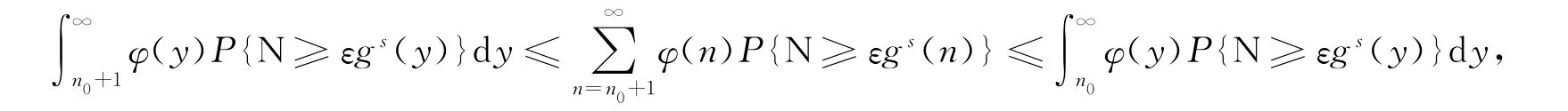
进一步有

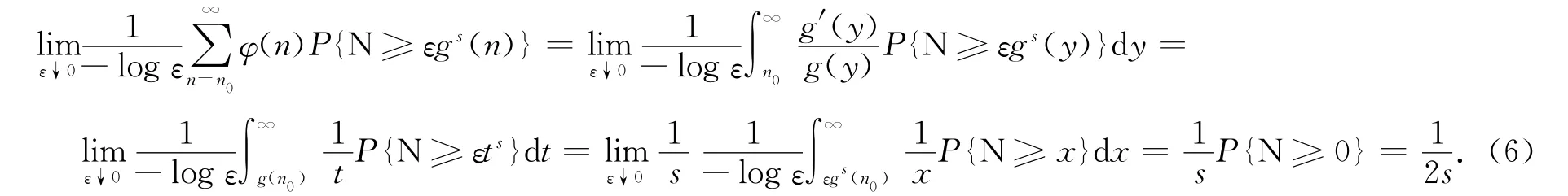
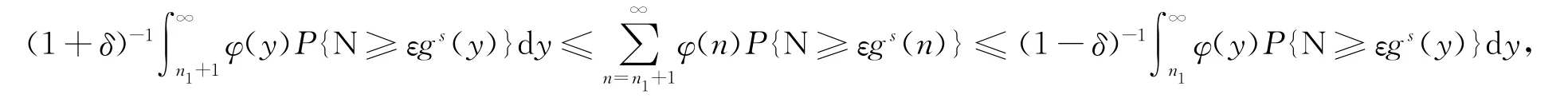
因此

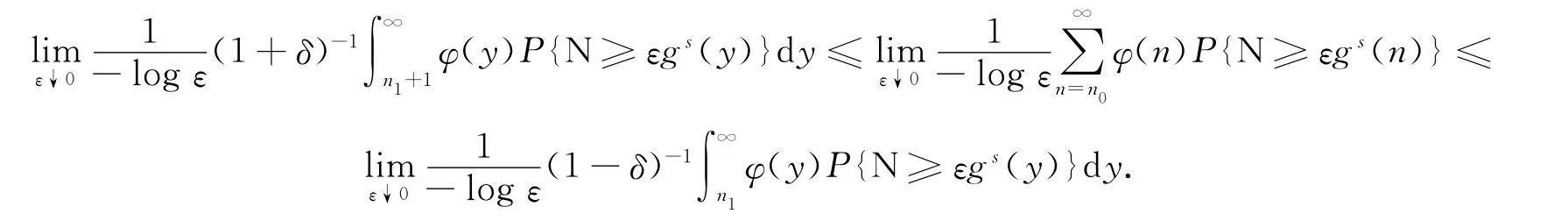
再由式（6）可知

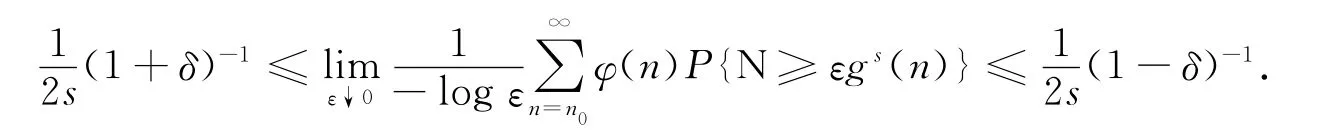
为简便，下面省略φ（x）的讨论过程.

命题2 在定理1的条件下，有：

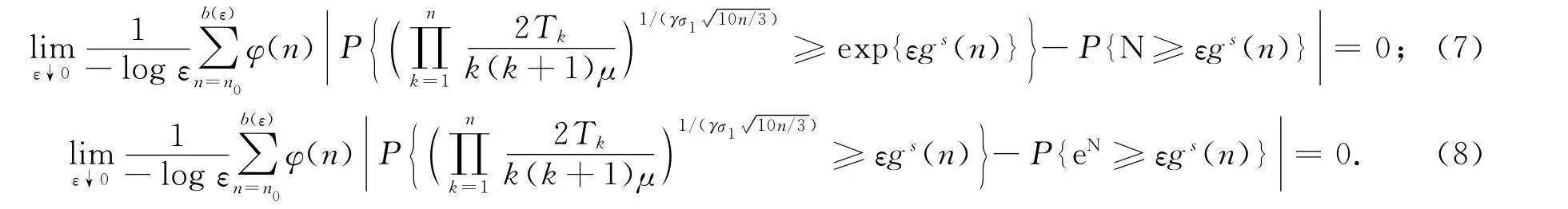
证明：只证式（8），式（7）可由式（8）推得.由引理1知

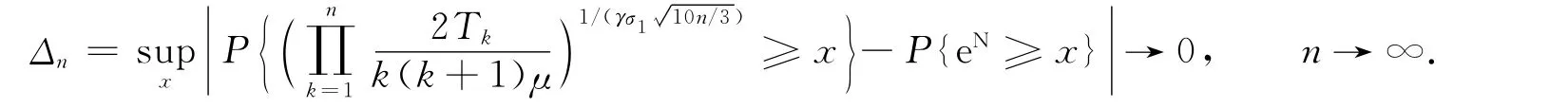
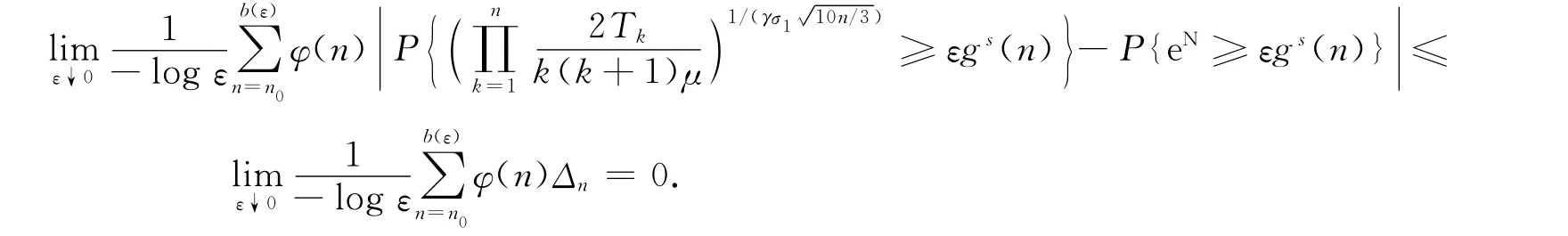
命题3 在定理1的条件下，有：

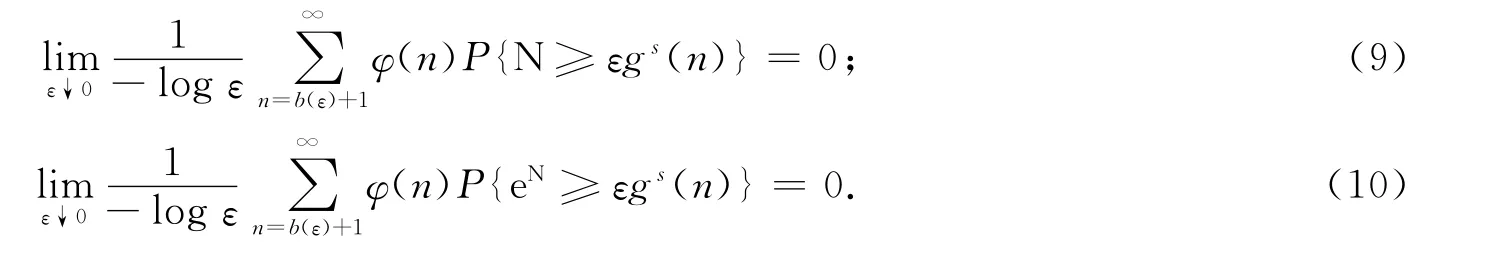
证明：只需证明式（10）成立，由式（10）可直接推得式（9）成立.由于当n＞b（ε）时有εgs（n）＞ε1－rs.利用L’Hospital法则，并注意到r＞1／s，类似命题1的证明，有

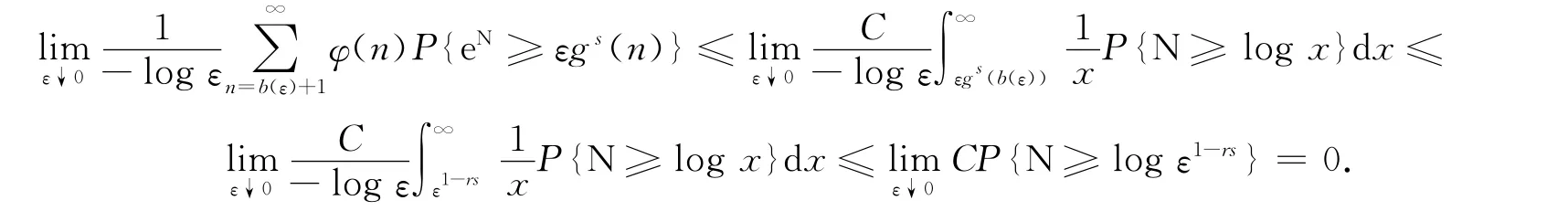
命题4 在定理1的条件下，有：

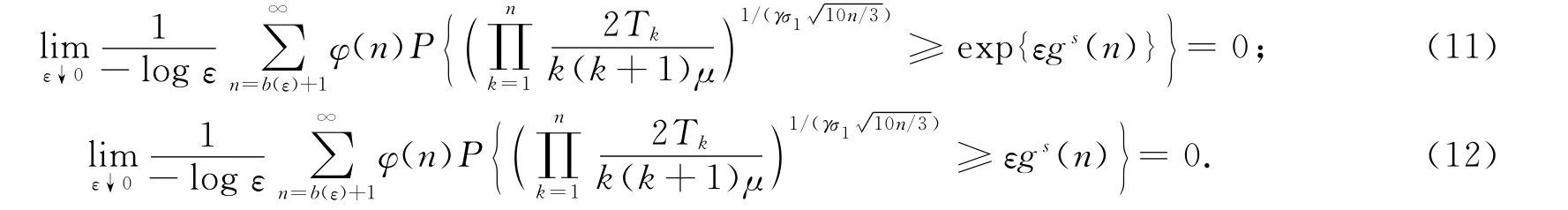
证明：由于由式（12）可直接推得式（11）成立，因此只需证明式（12）成立即可.由于当n＞b（ε）时，有εgs（n）＞ε1－rs，因此要证明式（12）成立，只需证明下式成立即可：

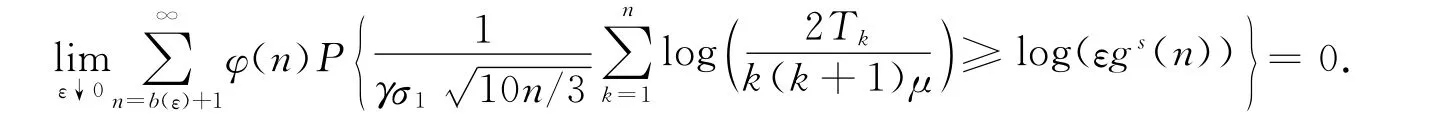
而对任意的x＞－1，都有log（1＋x）≤x.因此要证明式（12），只需证明下式成立：

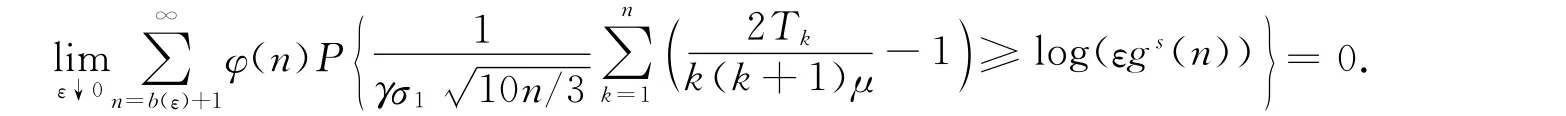
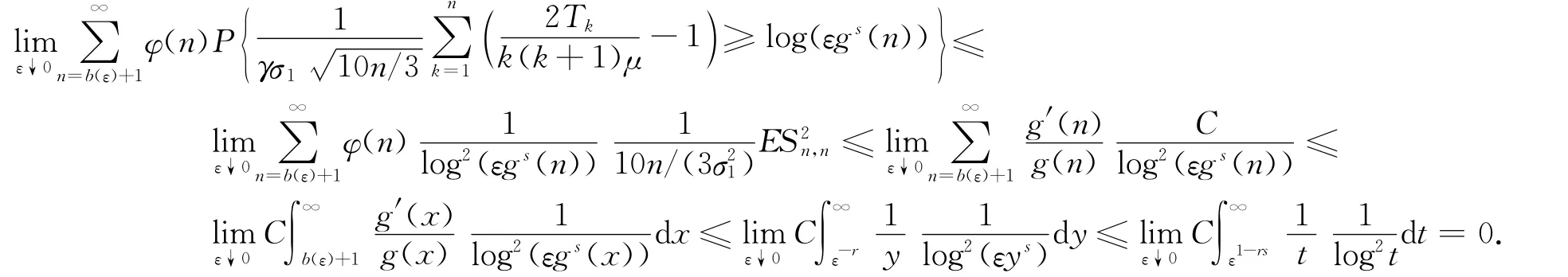
从而命题4成立.

由命题1～命题4及三角不等式可证明定理1成立.

2.2 定理2的证明

令d（ε）＝［g－1（Mε－1／s）］，其中g－1（x）为g（x）的反函数，M≥1.

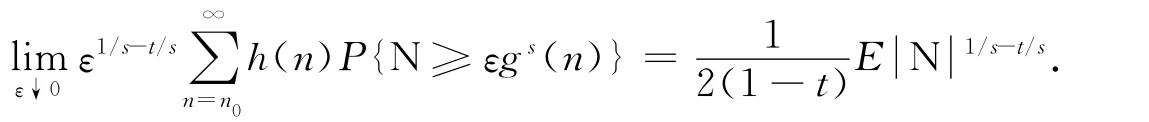
证明：类似命题1的证明，考虑积分和级数之间的关系.如果h（y）单调非增，则h（y）P｛N≥εgs（y）｝也单调非增，从而有

进一步有

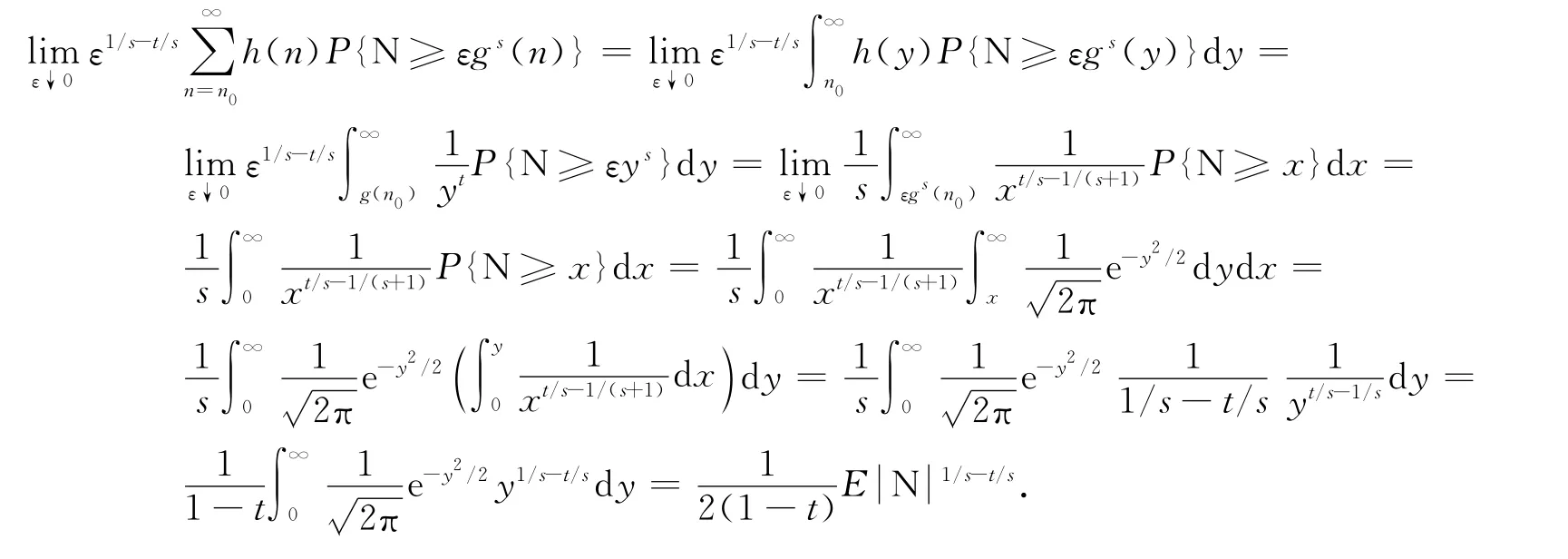
命题6 在定理2的条件下，有

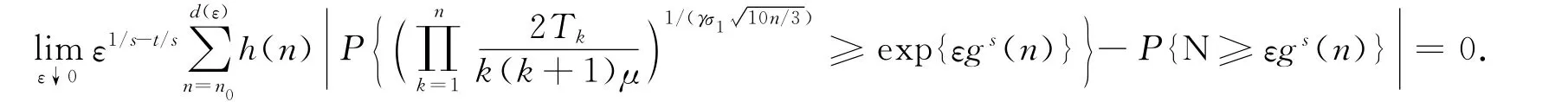
证明：由引理1，注意到假设条件（H1）和（H2），与命题2的证明过程类似可证.

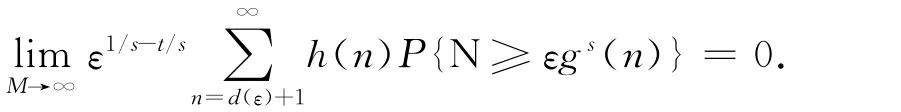
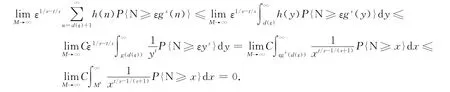
命题8 在定理2的条件下，有

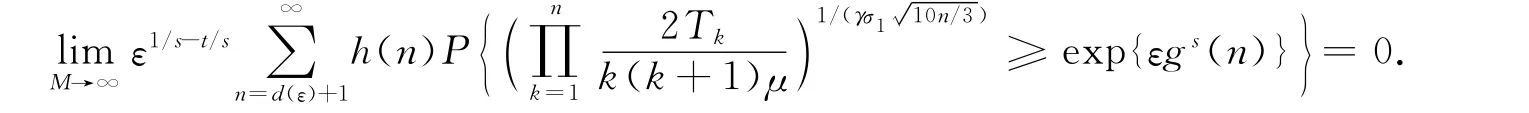
证明：与命题4的证明过程类似.

由命题5～命题8及三角不等式可证明定理2成立.

［1］杨金英.ρ－混合序列部分和之和乘积的渐近分布 ［J］.吉林大学学报：理学版，2012，50（2）：258－262.（YANG Jinying.Asymptotic Distribution of Products of Sums of Partial Sums underρ－Mixing Sequences ［J］.Journal of Jilin University：Science Edition，2012，50（2）：258－262.）

［2］付艳莉，吴群英.强混合序列部分和之和乘积的几乎处处中心极限定理 ［J］.山东大学学报：理学版，2010，45（8）：104－108.（FU Yanli，WU Qunying.Almost Sure Central Limit Theory for the Products of Sums of Partial Sums under Strong Mixing Sequences［J］.Journal of Shandong University：Natural Science，2010，45（8）：104－108.）

［3］ZHANG Yong，YANG Xiaoyun，DONG Zhishan.An Almost Sure Central Limit Theorem for Products of Sums of Partial Sums under Association［J］.J Math Anal Appl，2009，355（2）：708－716.

［4］Gut A，Spǎtaru A.Precise Asymptotics in the Baum－Katz and Davis Laws of Large Numbers［J］.J Math Anal Appl，2000，248（1）：233－246.

［5］Gut A，Spǎtaru A.Precise Asymptotics in the Law of the Iterated Logarithm ［J］.Ann Probab，2000，28（4）：1870－1883.

［6］ZHANG Yong，YANG Xiaoyun，DONG Zhishan.A General Law of Precise Asymptotics for the Complete Moment Convergence［J］.Chin Ann Math：Ser B，2009，30（1）：77－90.

［7］谭希丽，邢楠，董志山.B值m相依随机变量列生成平均移动过程精确渐近性的一般形式 ［J］.吉林大学学报：理学版，2011，49（1）：27－32.（TAN Xili，XING Nan，DONG Zhishan.General Result on Precise Asymptotics for Moving Average Processes of m－Dependent B－Valued Elements ［J］.Journal of Jilin University：Science Edition，2011，49（1）：27－32.）

［8］LI Jie.Precise Asymptotics of Moving Average Process underφ－Mixing Assumption ［J］.J Korean Math Soc，2012，49（2）：235－249.

［9］孙晓祥，杨丽娟.独立情形下一阶矩收敛的精确渐近性的注记 ［J］.吉林大学学报：理学版，2013，51（5）：871－875.（SUN Xiaoxiang，YANG Lijuan.A Note on the Precise Asymptotics for the First Moment Convergence of i.i.d.Random Variables［J］.Journal of Jilin University：Science Edition，2013，51（5）：871－875.）