参数空间中非自治四阶发展方程全局吸引子的存在性
徐海平, 李晓军 , 周康宝
(河海大学 理学院,江苏 南京210098)
1 引言及预备知识
考虑下面非自治四阶发展方程:
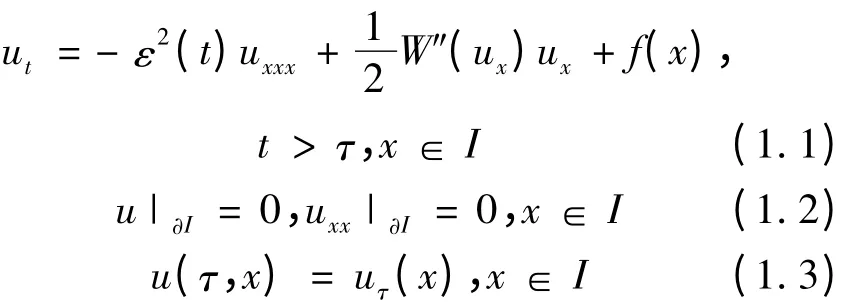
其中I = (0,1),W(p)= (p2-1)2,f(x)∈H10(I),ε(t)∈C1(I)为一非负有界递减函数满足:

且存在L >0,使得

此方程在弹性原理、相转换、图像处理等领域有着广泛的应用。当ε(t)= 0 时,系统是一个简单的模型描述了来自固-固相变在特定弹性晶体上的微结构,当ε(t)是不依赖于时间t 的常数时,在文献[1-3]中作者研究了(1.1)~(1.3)全局吸引子的存在性。文中考查系统(1.1)~(1.3)中ε(t)与时间t 有关,且由于ε(t)在无穷远处衰减为0,从而方程带有奇异性。这在运用经典的方法得到吸收集及吸引子的存在性时带来一定困难。为得到时间导数项或-Δ 项依赖于时间参数的波方程的全局吸引子的存在性,Temam 等人分别在文献[4-5]中将时间参数并入过程所定义的空间,给出在依赖于参数t的空间中全局吸引子的存在性。文中应用文献[4-5]中的理论,考察式(1.1)~(1.3)依赖于时间t 的全局吸引子的存在性。
对于任意的u ∈H2(I)∩),令‖·‖表示L2(I)范数,内积为<·,·>。则有
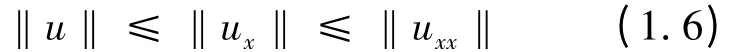
首先给出关于含参数空间的一些概念。对于每个对t ∈R,令Xt是一族依赖于时间t 的赋范空间,称双参数映射U(t,τ):Xτ→Xt是一个过程,若它满足:
1)U(t,τ)= U(t,r)U(r,τ),∀τ ≤r ≤t;
2)U(τ,τ)是Xτ上的恒同映射。
令
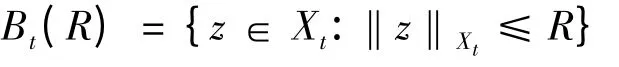
设A,B 的Hausdorff 半距离为

若对任意的t ∈R,存在Rt,使得Ct⊂Bt(Rt)成立,则称集族C = {Ct}t∈R在Xt中是有界的。
定义1.1 称有界的一族集合{Bt}t∈R是拉回吸收集,如果对任意的R >0,都存在t0= t0(t,R)≤t,使得

称过程U(t,τ)是耗散的,若其拥有一拉回吸收集。定义1.2 称集族{Kt}t∈R,Kt⊂Xt,是拉回吸引的,若对任意的ε >0,集族{(Kt)}t∈R是拉回吸收的,其中(Kt)是Kt在Xt中的ε-邻域。若过程U(t,τ)拥有一个非空紧的拉回吸引集,即{Kt}t∈R是拉回吸引的,Kt⊂Xt是Xt中的紧集,则称U(t,τ)是渐近紧的。
定义1.3 称{At}t∈R是过程U(t,τ)依赖于时间的全局吸引子,如果{At}t∈R是拉回吸引的,At⊂Xt是紧集。
为保证吸引子的不变特性,引入下面定义。定义1.4 称U(t,τ):Xτ→Xt是闭的,若对任意给定的t ≥τ,{xn}⊂Xτ,
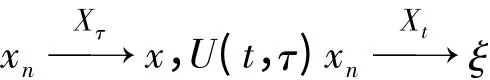
则有U(t,τ)x = ξ。
若对固定的T >0,U(t,t - T)是闭的,则称U(t,τ)是T-闭的。
由上述定义可知,连续过程,强弱连续过程,闭过程都是T-闭的。下面给出关于依赖时间的全局吸引子存在性的抽象结果,证明如同文献[6-8]。
定理1.1 假定过程U(t,τ):Xτ→Xt是渐近紧的,则存在依赖于时间的全局吸引子{At}t∈R,At⊂Xt。进一步假设U(t,τ)是T-闭的,则{At}t∈R满足不变特性:

注:上定理给出的全局吸引子没有唯一性,若过程U(t,τ)拥有一个一致有界的紧的拉回吸收集,则定理1.1 中所描述的全局吸引子在吸引意义下是唯一的。
2 主要结果
对于系统(1.1)~(1.3),令空间Xt为含参数的L2(I),定义空间Xt的范数为
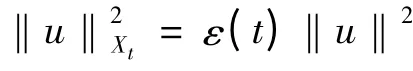
同理定义空间Yt= H2(Ω)×(Ω),范数为
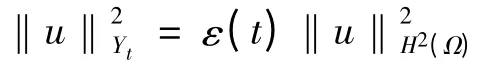
由ε(t)的假设可知,空间Xt与Xτ等价,空间Yt与Yτ等价,当t →+ ∞时,等价常数爆破。
由标准的Galerkin 方法(如见文献[9-14]),有如下结果。
定理2.1 假设式(1.2)~(1.5)成立,那么问题(1.1)~(1.3)在L2(I)中适定,即对任意的τ ∈R,任意的初值uτ∈L2(I)和任意的T ≥0,方程(1.1)~ (1.3)存在唯一的弱解u ∈C([τ,t];L2(I)),且该解连续地依赖于初值。
由上述定理可知,在Xt中可以定义过程U(t,τ):
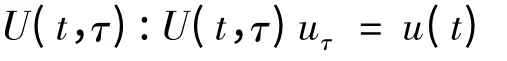
其中u(t)是系统(1.1)~(1.3)的解。
引理2.1 假设式(1.2)~(1.5)成立,则对Xτ中的任何有界集B = Bτ(R),存在τ0= τ0(B,t)>0,使得
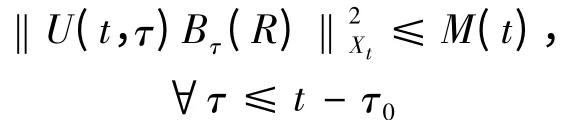
证 对式(1.1)两边用ε(t)u 在L2(I)中作内积,可得
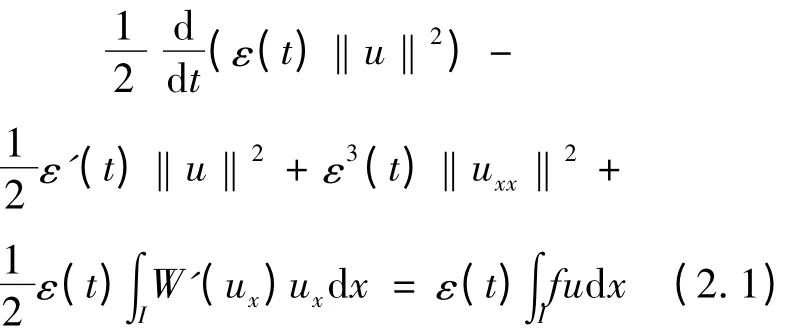
由ε(t)的假设,从上式可得

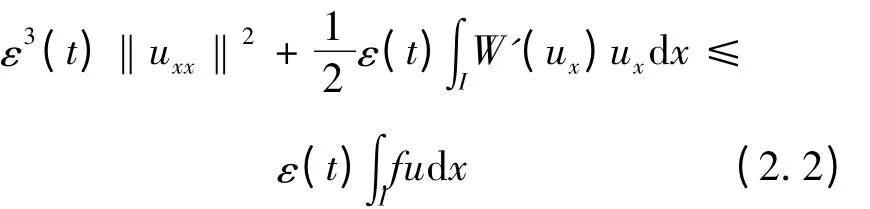
应用函数W 的假设,从式(2.2)可以得到
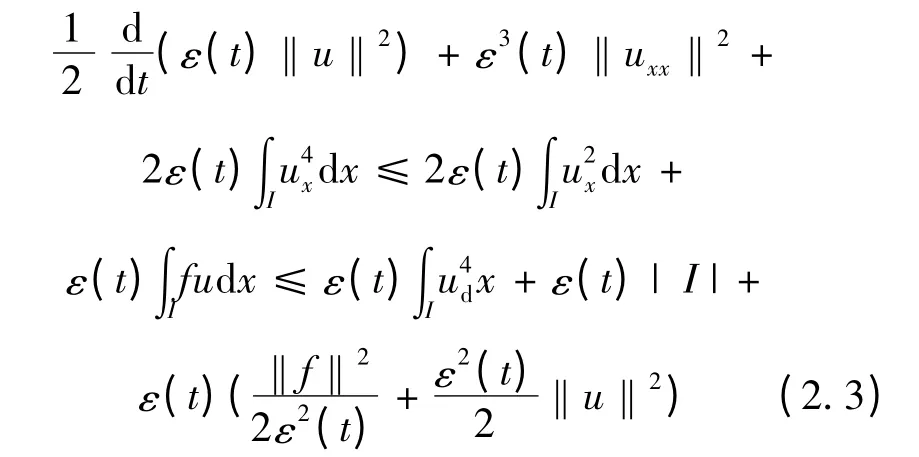
故由上式得
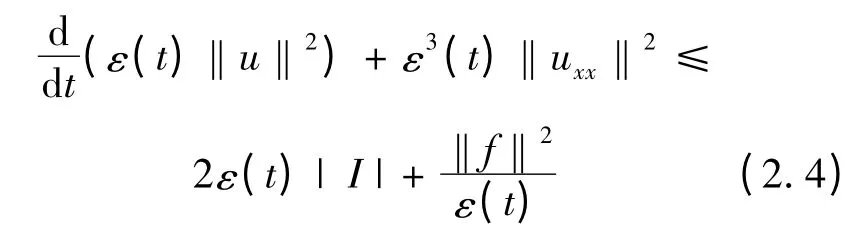
应用式(1.6)于式(2.4)并运用Gronwall 引理可得
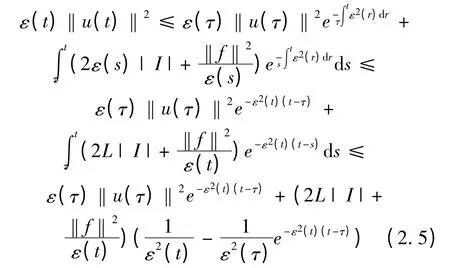
这里,用到ε(t)的假设。令τ →-∞时,由上式可得
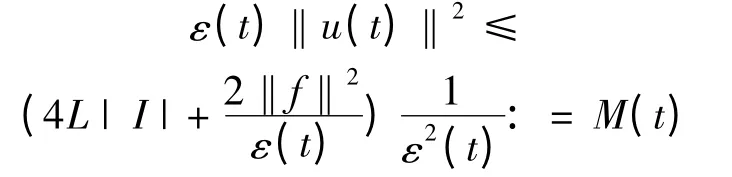
由引理2.1 可知,过程U(t,τ)存在一个有界的拉回吸收集{Bt}t∈R,其中

令初值u(τ,x)属于Bτ。应用引理2.1,并对式(2.4)在(t,t +1)上积分可得
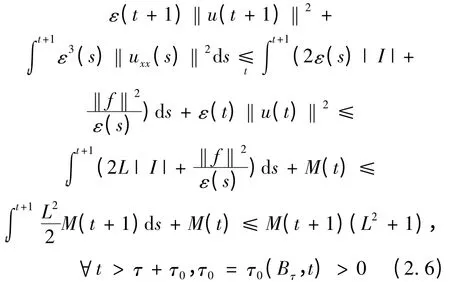
令‖·‖4表示L4(I)的范数。由式(2.3)可得
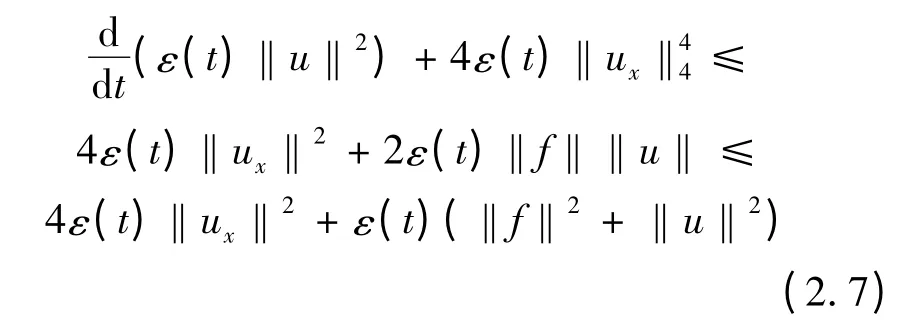
对式(2.7)在(t,t +1)上积分可得
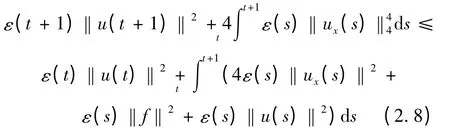
应用式(2.6)于由式(2.8)可得
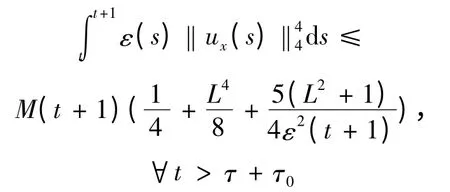
因此

引理2.2 假设式(1.2)~式(1.5)成立,则对任意的uτ∈Bτ,存在τ0= τ0(t,Bτ)>0,使得
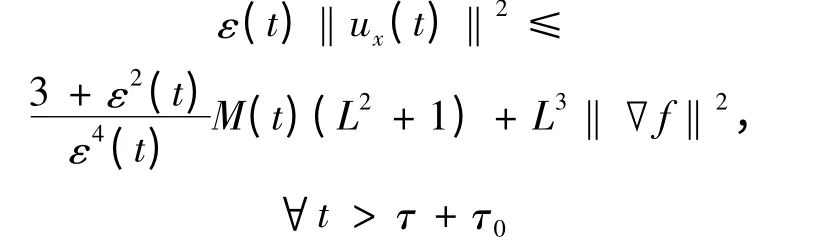
证 用- ε(t)uxx对式(1.1)在L2(I)中做内积可得
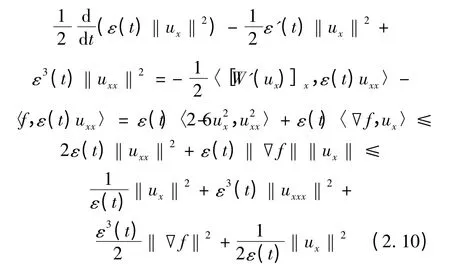
由此可以推导出

对式(2.11)在(s,t + 1)上积分,且s ∈(t,t +
1),可得
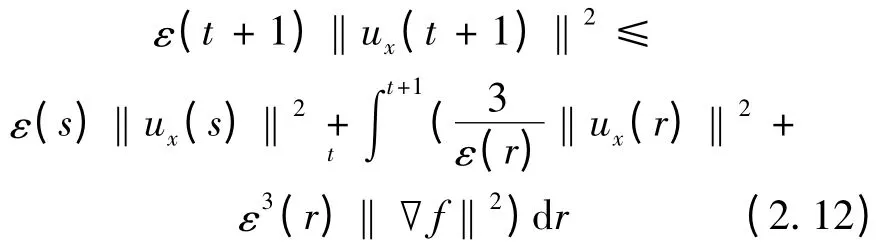
对式(2.12)再关于s 在(t,t +1)积分得

此外,重新估计式(2.10)可得
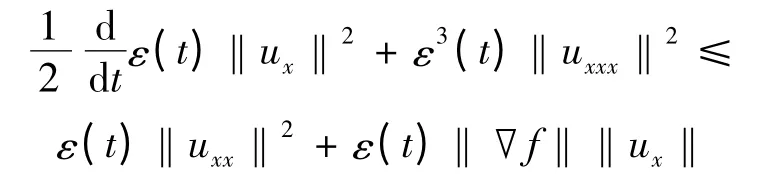
固有
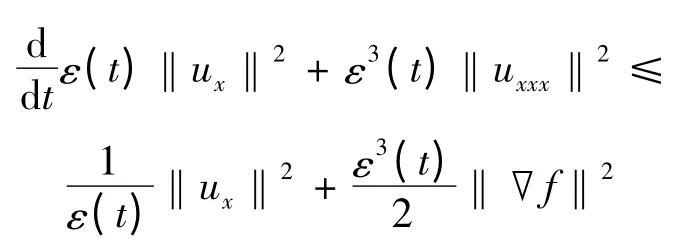
对上式在(t,t +1)上积分可得

引理2.3 假设式(1.2)~(1.5)成立,则对任意的uτ∈Bτ,有
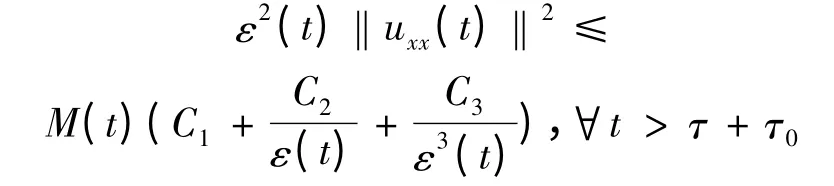
其中Ci,i = 1,2,3,为正常数。
证 用ut对式(1.1)在L2(I)中做内积可得

对式(2.15)在(s,t +1)积分,且t ≤s ≤t +1,可得
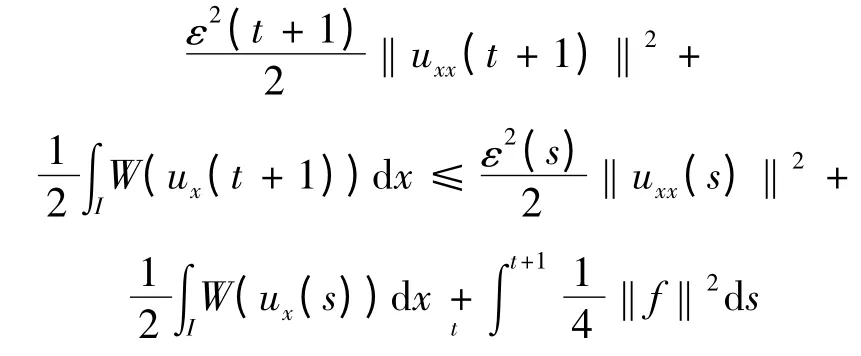
对上式再关于s 在(t,t +1)上积分得

结合式(2.6)和式(2.9)可得
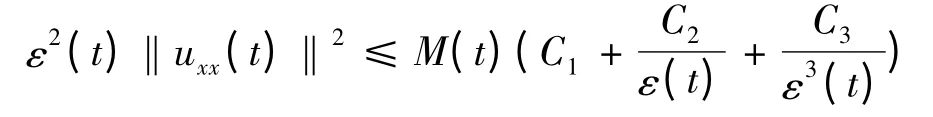
定理2.2 假设式(1.2)~式(1.5)成立,则式(1.1)~式(1.3)所对应的过程在Xt中有依赖于时间的全局吸引子{At}存在,且At于Yt中有界。
证 由引理2.1 可得过程在Xt中有一个依赖于时间的吸收集。由引理2.2 ~2.3 可得系统所对应的过程在Xt中是渐近紧的。利用定理2.1 及定理2.2,可以得到过程在Xt中有依赖于时间的全局吸引子{At}t∈R存在。
[1]Colucci R,Chacón G R.Asymptotic behavior of a fourth order evolution equation[J]. Nonlinear Analysis:Theory,Methods and Applications,2014,95:66-76.
[2]Caraballo T,Colucci R. Pullback attractor for a non-linear evolution equation in elasticity[J]. Nonlinear Analysis:Real World Applications,2014,15:80-88.
[3]Colucci R,Chacón G R.Hyperbolic relaxation of a fourth order evolution equation[J].Abstract and Applied Analysis,2013,23(1):666-686.
[4]Conti M,Pata V,Temam R. Attractors for processes on time-dependent spaces. Applications to wave equations[J]. Journal of Differential Equations,2013,255(6):1254-1277.
[5]Di Plinio F,Duane G S,Temam R. Time-dependent attractor for the Oscillon equation[J]. arXiv preprint arXiv:1009.2529,2010.
[6]García-Luengo J,Marín-Rubio P,Real J. Pullback attractors in V for non-autonomous 2D-Navier-Stokes equations and their tempered behaviour[J].Journal of Differential Equations,2012,252(8):4333-4356.
[7]Marín-Rubio P,Real J. On the relation between two different concepts of pullback attractors for non-autonomous dynamical systems[J].Nonlinear Analysis:Theory,Methods and Applications,2009,71(9):3956-3963.
[8]Caraballo T,Łukaszewicz G,Real J. Pullback attractors for asymptotically compact non-autonomous dynamical systems[J].Nonlinear Analysis:Theory,Methods and Applications,2006,64(3):484-498.
[9]Robinson J C.Infinite-Dimensional Dynamical Systems:an Introduction to Dissipative Parabolic PDEs and the Theory of Global Attractors[M].Cambridge:Cambridge University Press,2001.
[10]Temam R.Infinite Dimensonal Dynamical Systems in Mechanics and Physics[M].Berlin:Springer Science and Business Media,1997.
[11]Cheban D N,Kloeden P E,Schmalfuβ B. The relationship between pullback,forwards and global attractors of nonautonomous dynamical systems[J].Nonlinear Dyn Syst Theory,2002,2(2):125-144.
[12]Babin A V,Vishik M I.Attractors of Evolution Equations[M].Amsterdam,Holland:Elsevier,1992.
[13]姚庆六.一类非线性四阶三点边值问题的可解性[J].山东大学学报:理学版,2006,41(1):11-15.
YAO Qingliu. Solvability of a class of nonlinear fourth-order three-point boundary value problems[J]. Journal of Shandong University,2006,41(1):11-15.(in Chinese)
[14]徐茜,李晓军.带非线性阻尼非自治波方程拉回吸引子的存在性[J].黑龙江大学自然科学学报,2004,31(3):306-314.
XU Qian,LI Xiaojun.The existence of pullback attrators for non-autonomous wave equations with nonlinear damping[J].Journal of Natural Science of Heilongjiang University,2004,31(3):306-314.(in Chinese)

