可解多项式代数上的泛左Gröbner基
尹杰杰,王汇宇
(海南大学 信息科学技术学院,海南 海口 570228)
可解多项式代数上的泛左Gröbner基
尹杰杰,王汇宇
(海南大学 信息科学技术学院,海南 海口 570228)
设I是可解多项式代数A=K[a1,…,an]的一个非零左理想,由可解多项式代数上的左Gröbner基性质,可知A中任何一个左理想对于一个单项式序的左Gröbner基不一定满足另一个单项式序.首先证明了在B上的任意2个单项式序1,2下,g={g1,g2,…,gt}是I在1下的左Gröbner基,若LM(gi)=LM(gi),1≤i≤t,那么g={g1,g2,…,gt}也是I在2下的左Gröbner基;其次证明了I在A上的所有单项式序(可能无限个)下只有有限个约化左Gröbner基;最后证明了A中的一个子集F,对于其上的任何一个单项式序,都是I的左Gröbner基,子集F就是A的泛左Gröbner基.
可解多项式; 单项式序; 左理想; 左Gröbner基
Gröbner基是Buchberger[1]在研究域上多变元多项式的理想生成元问题的博士论文中提出的,并以他的导师Gröbner W 的名字命名.Gröbner基理论最重要的贡献是能计算且可求出来.自Buchberger创立交换多项式左理想的Gröbner基理论及其算法以来,该方法对于解决交换与非交换数学领域的实际问题有着十分广泛的应用.如多项式左理想的Gröbner基方法在判别多项式方程组解的存在性[2],在解存在的情况下判别解的个数的有限性以及在求解过程中的有效性是众所周知的事实.该方法已经被国内外数学工作者广泛应用.因此其一出现,不仅受到代数学界的重视,而且受到数学界、应用数学界、计算机科学界和系统科学界等研究领域的重视,理论方面和应用方面都得到了迅速的发展.由于实际问题规模的巨大,考虑到方程组的稀疏性,相应地产生了可解多项式中的Gröbner基的问题,对其进行研究,可以提高计算的效率.
本文给出了可解多项式代数A中的左Gröbner基的性质,得出了其中任何左理想对于一个单项式序的左Gröbner基不一定满足另一个单项式序,首先证明了在B上的任意2个单项式序1,2下,g={g1,g2,…,gt}是I在1下的左Gröbner基,若LM(gi)=LM(gi),1≤i≤t,那么g={g1,g2,…,gt}也是I在2下的左Gröbner基;然后证明了I在A上的所有单项式序(可能无限个)下只有有限个约化左Gröbner基;最后证明了A中的一个子集F,对于其任何一个单项式序,都是I的左Gröbner基,子集F就是止的泛左Gröbner基.
1 预备知识
本节简单介绍有关可解多项式代数中左Gröbner基的一些基本概念和结果,主要参考文献[3-7].

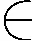
f的首单项式为LM(f)=aα(m);
f的首项系数为LC(f)=λm;
f的首项为LT(f)=λmaα(m).
在计算代数中将B中元素称为单项式,用小写字母u,v,w,s,…来表示B中单项式.
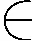
定义1设有限生成K-代数A有一个PBWK-基B,是B上一个全序关系.若满足以下条件
定义2设有限生成K-代数A有一个PBWK-基B,是B上一个单项式序.如果对于任意u=aα,v=aβB有uv=aαaβ=λα,βaα+β+fα,β,其中λα,βK*,fα,βA满足LM(fα,β) 定义3设为B上一个单项式序,对于u,vB,如果存在wB,使得v=LM(uw),则称u左整除v,记为u│lv;如果存在wB,使得v=LM(uw),则称u右整除v,记为u│rv;如果存在w,sB,使得v=LM(wus),则称u整除v,记为u│v. 1)g是I的一个左Gröbner基; 称为f与g的左S-元. 定理7设是B上给定的单项式序是g生成的A左理想,那么g={g1,…,gt}是I的关于的一个左Gröbner基当且仅当对所有的gi≠gj,用g中的元素对S(gi,gj)g做除法后使得所有的S(gi,gj)都约化到零,即 Buchberger算法: AlgorithmI: Input:F={f1,…,fm}⊂K[a1,…,an],其中fi≠0 Whileg≠∅ Do S:=S-{S(f,g)} Ifh≠0 Then g:=g∪{h} End End 1) g是I的一个极小左Gröbner基; 则称g为I是A的一个约化左Gröbner基. 定义10设I是A的一个非零左理想,是B上的一个单项式序.则在下I有唯一一个约化左Gröbner基. 定义11设I是A=K[a1,…,an]的一个左理想,F是I的子集,若F对K[a1,…,an]上的每一个项序都是I的Gröbner基,则称F是I的泛Gröbner基. 定理1设I是K[a1,a2,…,an]的一个左理想,1,2是B上的2个单项式序,g={g1,g2,,…,gt}是I在1下的左Gröbner基,如果LM(gi)=LM(gi),1≤i≤t,那么g={g1,g2,…,gt}也是I在2下的左Gröbner基. 证明因为I是K[a1,a2,…,an]的一个左理想,1,2是B上的2个单项式序,g={g1,g2,…,gt}是I在1下的左Gröbner基,所以∀fI,在单项式序1下有 令LM(f)=aα(1),且有在1下f模g约化为0,可知aα(i)I,1≤i≤m. 令LM(f)=aβ(1)=aα(r),其中1≤r≤m.∃gj,1≤j≤t,有LM(gj)│laα(r),所以有LM(gj)│laα(r),所以LM(gj)│laβ(1),故有LM(gj)│lLM(f),且可以得到在2下f模g约化为0.所以G也是I在2下的一个左Gröbner基. 定理2设I是K[a1,a2,…,an)]的一个非零左理想,令T为B上所有(无限多个)单项式序的集合,对于每个单项式序T,令〈LM(I)〉为I上的首单项式生成的单项式左理想,g为I在下的既约左Gröbner基.进而令L={〈LM(I)〉│T},R={g│T},有1)存在R到L的一一映射;2)L是一个有限集,R也是一个有限集. 证明1)I是K[a1,a2,…,an]的一个非零左理想,T为B上所有单项式序的集合. L={〈LM(I)〉│T},R={g│T}令 φ:R→L,g→〈LM(I)〉, g是I在下的既约左Gröbner基,〈LM(I)〉为I上的首单项式生成的单项式理想. 令g,gR,且g≠g,则〈LM(g)〉≠〈LM(g)〉,所以φ是单射. 综上所述,R到L是一一映射. 2)假设L是一个无限集.L={〈(LM(I)〉│T},从L中任意取出一个首项理想〈LM(I)〉,满足该首项理想〈LM(I)〉的单项式序有无限个. 取T0⊆T,其中T0是满足首项理想〈LM(I)〉的所有单项式序构成的集合.显然T0是一个有限集. 令g={f1,f2,…,fs},设多项式fi有ki项,1≤i≤s,所以LM(fi)在不同的单项式序下最多有ki个不同的首项1≤i≤s,所以LM(g)在不同的单项式序下最多有kik2…ks个不同的LM(g).由此可知LM(g)不相同的单项式序最多也只有kik2…ks,是有限的. 又因为〈LM(g)〉是由LM(g)生成的左理想,故可知左理想〈LM(g)〉互不相同的单项式序也是有限的. 取无限集T1⊆T0,使得在T1中的所有项序下都有LM(f1)=m1; 取无限集T2⊆T1,使得在T2中的所有项序下都有LM(f2)=m2; 取无限集T3⊆T2,使得在T1中的所有项序下都有LM(f3)=m3; ⋮ 取无限集Ts⊆Ts-1,使得在T1中的所有项序下都有LM(fs)=ms;因为Ts⊆Ts-1⊆ … ⊆T3⊆T2⊆T1⊆T0,所以在无限集Ts的所有项序下都有LM(fi)=mi,1≤i≤s; 由定理1可知,在Ts的所有项序下,g都是I的左Gröbner基.又因为〈LM(I)〉=〈m1,m2,…,ms〉,所以〈LM(I)〉是有限的,矛盾,故L是有限集. 又因为〈LM(I)〉=〈m1,m2,…,ms,ms+1,…,mr〉所以〈LM(I)〉是有限的,矛盾. 综上所述,假设不成立,L为有限集. 由1)可知R到L是一一映射的,所以R也是一个有限集.得证. 因为R={g│T},且R是一个有限集,所以可知I只有有限多个约化左Gröbner基. 定理3左理想I一定存在子集F,对于A的每一个单项式序都是I的左Gröbner基[7]. 证明由定理2,可设(G1,1)={g11,g12,…,g1k1},(G2,2)={g21,g22,…,g2k2},(G3,3)={g31,g32,…,g3k3},…,(Gs,s)={gs1,gs2,…,gsks}分别是I关于单项式序1,2,3,…,s的约化左Gröbner基,故对任何单项式序,I的约化左Gröbner基一定重合于G1,G2,…,Gs之中的一个.令F={g11,g12,…,g1k1,…,gs1,gs2,…,gsks},则可知对任何单项式序,F都是I的约化左Gröbner基.得证. 此时可知F就是I的泛左Gröbner基. 设I=〈xy-x,x-y2〉⊆Q[x,y],找出I的泛左Gröbner基,只需要找出I的全部有限个约化左Gröbner基.只要根据Buchberger算法,对一切可能的项序求出I的既约左Gröbner基,其泛左Gröbner基即可求出为F={x-y2,xy-x,y3-y2,x2-x}. [1]BuchbergerB.EinAlgorithmuszumAuffindenderBasiselementedesRestklassenringesnacheinemnulldimensionalenpolynomideal[D].Innsbruck:Universityoflnnsbruck,1965. [2] 熊雪玮,赵志琴.图的k-独立集与Gröbner基求解[J].工程数学学报,2012,29(5):696-702. [3]AdamsW,LoustaunausP.AnintroductiontoGröbnerbases[M].Washington,DC:AmericanMathematicalSociety,1994. [4] 刘木兰.Gröbner基理论及其应用[M].北京:科学出版社,2000. [5]LiH,WuY.Filtered-gradedtransferofGröbnerbasiscomputationinsolvablepolynomialalgebras[J].Corem.Alg.2000,28(1):15-32. [6]LiH.NoncommutativeGröbnerbasesandFiltered-GradedTransfer[M].Berlin:Springer-Verlag,2002. [7] 安立奎, 韩丽艳.半群代数K[A]中的泛Gröbner基的研究[J].渤海大学学报(自然科学版),2005,26(4):331-332. Universal Left Gröbner Bases on Solvable Polynomial Algebra Yin Jiejie,Wang Huiyu (Department of Information and Technology College, Hainan University, Haikou 570228, China) In the report, let I be a nonzero left ideal of a solvable polynomial algebraA=K[a1,…,an], based on the property of left Gröbher of the solvable polynonlial algebra,we know that a len Gröbner bases with respect to one monomial ordering might not be a left Gröbner bases with respect to another monomial ordering.First, it was proved that1,2,B,g={g1,g2,…,gt}, is the left Gröbher bases ofIwith respect to1, if LM(gi)=LM(gi), 1≤i≤t, theng={g1,g2, …,gt} is also the left Gröbher bases ofIwith respect to2; Second, it was proved that there are only finitely many possible reduced left Gröbner bases for a given left ideal; Last, a subset ofA,f, is a left Gröbner bases with respect to every ordering, and which is called a universal left Gröbner bases ofA. solvable polynomial algebra; monomial ordering; left ideal; left Gröbner bases 2015-05-11 尹杰杰(1990-),男,广东韶关人,2012级硕士研究生,研究方向:计算代数,E-mail:15120644019@163.com 1004-1729(2015)04-0305-05 O 157.5 A DOl:10.15886/j.cnki.hdxbzkb.2015.0054






2 主要结论和证明
3 实验举例

