基于RMC程序的keff对核数据的敏感性分析

丘意书，余健开，梁金刚，王 侃

(清华大学 工程物理系，北京 100084)

基于RMC程序的keff对核数据的敏感性分析

丘意书，余健开，梁金刚，王 侃

(清华大学 工程物理系，北京 100084)

适用于连续能量蒙特卡罗程序的敏感性分析方法是当前的研究热点。本文建立了5种不同反应类型的敏感性系数的计算公式，对当前应用广泛的反复裂变几率法的理论基础及算法进行了分析。分别使用RMC程序和MCNP6程序计算了keff对核数据的敏感性系数，计算结果吻合良好。本文结果表明RMC程序初步具备了敏感性分析的功能。

敏感性分析；反复裂变几率法；连续能量；RMC程序

当使用测量仪器或数值方法得到某个物理量的估计值时，需要知道它离真值多近，估计值和真值的差异用误差来表示。然而，真值往往是未知的或不可知的，一般只能估计误差的大小，对误差的估计称之为不确定度。不确定性分析的任务就是分析由输入(例如核数据因测量引起)的不确定度导致计算结果(keff等)的不确定度。

不确定性分析的方法一般包括两类。第1类是随机抽样法，根据方差及协方差的大小抽样输入参数，产生无穷多个输入系列，进行输运计算，然后对计算结果进行统计分析，得到keff的不确定度，代表程序为德国核设备与反应堆安全研究协会(GRS)研制的XSUSA程序[1]。该方法简单，容易实现，但需非常大的计算量。第2类方法是基于敏感性分析的方法。该方法需先计算出keff对核截面的敏感性系数，再结合截面的协方差数据库计算出keff的不确定度。这类方法计算效率高，是当前用于keff对核数据不确定性分析的主要方法，代表程序为美国橡树岭国家实验室(ORNL)开发的SCALE6.1程序包[2]中一维敏感性与不确定性分析模块TSUNAMI-1D和三维敏感性与不确定性分析模块TSUNAMI-3D。TSUNAMI-1D和TSUNAMI-3D的输运计算分别使用的是SN程序XSDRNPM和蒙特卡罗程序KENO，它们的共同点是基于多群截面数据库，需要执行并群和共振自屏计算，因而必须计算隐式敏感性系数，以考虑多群近似对敏感性系数的影响。另外，需要执行一次前向计算和伴随计算分别获得通量和伴随通量的信息。

为使计算流程更加简单及使计算结果更加可靠，使用连续能量蒙特卡罗程序计算keff对核数据的敏感性系数，成为近几年蒙特卡罗方法研究的热点。然而，现有基于多群蒙特卡罗程序的敏感性分析方法无法适用于连续能量蒙特卡罗程序中，因为在执行伴随蒙特卡罗计算时对连续能量的中子散射算符进行转置非常困难。因此，需要提出新的适用于连续能量蒙特卡罗框架的计算敏感性系数的方法。这些方法包括微分算符抽样法(DOS)[3]、反复裂变几率法(IFP)[4]、次级粒子贡献法(Contributon)[5]、CLUTCH法[6]及Contributon-IFP混合法[7]。其中，反复裂变几率法最先在计算动态参数上获得应用[8]，被用于敏感性分析研究[6，9-10]。由于该方法物理概念清晰，计算精度高，几乎被现在所有具备敏感性分析功能的连续能量蒙特卡罗程序(MCNP6.1[11]、SCALE[7]及McCARD[12]程序)所采用。因而，本文选用该方法进行keff敏感性分析。

1 理论基础

基于一阶线性微扰理论[13]，从中子输运方程和伴随方程可推导得到由核数据的扰动引起的keff的扰动为：

(1)

其中：Ψ为通量；Ψ*为伴随通量；k表示keff；Σt为宏观总截面；S为散射算符；F为裂变算符；尖括号表示对相空间进行积分。

敏感性系数定义为某个核数据的相对变化量所引起的keff的相对变化量，如式(2)所示。

(2)

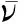
根据敏感性系数的定义及式(1)可得：

(3)

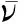
(4)

下面分别给出上述5种不同反应类型的敏感性系数的计算公式。

keff对吸收反应的敏感性系数为：

(5)

(6)

其中：g为能群号；z为所关心的区域；V为体积；Σa为吸收截面；Σf为裂变截面；E′为引起裂变的中子的能量；Ω′为引起裂变的中子的方向角；E为裂变产生的中子的能量；Ω为裂变产生的中子的方向角；D为伴随通量加权的裂变源项。

keff对散射反应的敏感性系数为：

(7)

其中，Σs，g为能群g的散射截面。式(7)中第1项代表了玻尔兹曼方程中的散射项对所求的敏感性系数的贡献，第2项代表了玻尔兹曼方程中的碰撞项对该敏感性系数的贡献。

keff对裂变反应的敏感性系数为：

(8)

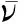
dΩ′dΩdE′dVdE

(9)

keff对裂变中子能谱χ的敏感性系数为：

(10)

与前4类敏感性系数不同，计算keff对χ的敏感性系数需对出射能量划分网格。

2 反复裂变几率法

2.1 理论基础

早在1964年，Hurwitz[14]就已指出，反复裂变几率与伴随通量呈正比，其物理含义为引入反应堆的某个中子在无穷远代产生的裂变次数。

伴随方程可写为：

(11)

其中，L*为伴随算符。

使用源迭代法求解伴随通量，第n代的伴随通量的解为：

(12)

(13)

(14)

其中，Ln(P→P′)表示相空间P的父代中子在P′处产生的第n代裂变中子。

因此，伴随通量可用反复裂变几率来表示。经数值验证，在连续能量蒙特卡罗程序中，一般取n=10可使大部分系统的反复裂变几率收敛。

2.2 算法实现

反复裂变几率法是使用反复裂变几率作为伴随通量的估计值的方法，该方法直接在前向输运计算中统计得到反复裂变几率的大小，不需求解共轭方程而额外执行1次伴随计算。根据反复裂变几率的物理含义，可人为地将蒙特卡罗模拟的活跃代划分为连续的块，每个块的大小为n，应使得伴随通量收敛。每个块的第1代称为初始代，初始代的裂变中子为父代中子，这些父代中子会产生子代中子，足够多的过渡代后(共n-2代)，父代中子产生的子代中子的数量会趋于稳定，此时，对应的活跃代称为渐进代，也就是每块的最后1代。根据敏感性系数的计算公式，在初始代统计特定核素、特定反应类型的反应率，在渐进代统计对应的反复裂变几率。具体的实现可使用伴随权重计数法，不需直接计算出伴随通量，因而无须对空间、能群、角度进行离散，计算精确高。

伴随权重计数原理如图1所示。在初始代，需定义父代中子的轨迹，它定义为父代中子出生地点和源中子之间的轨迹，如图1所示，源中子发生了两次裂变，因而可定义两条父代中子轨迹，分别是T1及T1+T2。根据所统计敏感性系数的类型，可分别获得δT1和δ(T1+T2)的贡献，再结合径迹长度估计法可获得初始代中反应率的估计值。其中，如果发生了所统计的敏感性系数的反应，δ等于1，否则为零。同时，为了跟踪后代中子，对每个父代中子进行编号。图1中两个祖先中子的编号分别为1和2。在过渡代，通过让所有后代中子继续父代中子编号的方法，跟踪父代中子产生的子代中子。在渐进代，统计这些父代中子所对应的子代中子(具有相同编号)引起的裂变以作为伴随权重的大小，图1中分别对应Q1及Q2+Q3。则两个父代中子的计数分别为T1Q1和(T1+T2)、(Q2+Q3)。

图1 伴随权重计数原理Fig.1 Scheme of adjoint weighted tally

3 计算结果

根据上述基本原理，基于清华大学工程物理系研制的自主堆用连续能量蒙特卡罗程序RMC[15]，使用反复裂变几率法开发了keff对核数据的敏感性分析功能，并将RMC的计算结果与MCNP6的进行比较。RMC的版本为RMC2.0，MCNP6为2013年发布的MCNP6.1。选取一个3×3燃料栅格作为验证基准题[16]，它的几何构造如图2所示。使用了27个不同的核素对该基准题进行建模。表1列出RMC和MCNP6的keff的计算结果，计算条件为每代200 000个粒子，非活跃代275代，一共20 275代，RMC和MCNP6的keff小于1 pcm。

为了统计敏感性系数，将活跃代划分成块，块大小取为10。表2列出RMC和MCNP6计算得到的重要核数据的敏感性系数。表2中，C/E定义为RMC与MCNP6的敏感性系数的比值。从表2可见，C/E的比值整体在1附近，两个程序计算结果总体吻合良好。keff对235U的平均裂变中子数最为敏感，约0.93。另外，RMC和MCNP6均满足keff对所有裂变核素的平均裂变中子数的敏感性系数之和等于1的检验标准。

图2 基准题几何Fig.2 Geometry of benchmark

表1 keff的计算结果Table 1 Calculation results of keff

表2中，两个程序所得的敏感性系数的相对偏差相当，表明它们的计数效率相当。与一般的蒙特卡罗计数不同，使用蒙特卡罗统计得到的敏感性系数并非其值越小，其相对偏差就一定越大。相对偏差的大小既与敏感性系数本身的大小有关，同时也与计数的方法有关。对于吸收反应类型，由于其敏感性系数只由碰撞项构成，两个程序均采用径迹长度法，抽样效率较高。对于散射及裂变反应类型，其敏感性系数不仅包括碰撞项，还包括散射或裂变项，RMC使用碰撞估计法对它们进行统计，而MCNP6采用平均估计法统计。由于采用不同的统计方法，敏感性系数的相对偏差也就不同。例如，尽管表2中keff对1H弹性散射截面的敏感性系数比(n,γ)的敏感性系数要大，但是其相对偏差也较大。

表2 不同核数据的敏感性系数Table 2 Sensitivity coefficients for different types of nuclear data

表3列出RMC和MCNP6计算得到的重要核素的总截面的敏感性系数。由表3可见，keff对235U、238U、1H 和10B 4种核素最为敏感。其中，keff对235U和1H的总截面的敏感性系数是正值，而对238U和10B的总截面的敏感性系数是负值。因为235U所有截面中对keff影响最大的是裂变截面，1H所有截面中对keff影响最大的是散射截面，它们均与keff正相关，而238U和10B所有截面中对keff影响最大的是(n,γ)截面，它与keff负相关。

图3示出235U和238U的重要敏感性系数曲线，能量网格的划分与SCALE6程序中的AMPX多群数据库中的中子238群能群结构一致。从图3a可看出，keff对235U裂变截面的敏感性系数与它对235U平均裂变中子数的趋势基本一致，在低能区出现峰值，这与235U容易发生裂变的能量范围一致，而(n,γ)截面的敏感性系数在热能区出现谷值，表明在低能区235U的吸收截面较大。从图3b可看出，keff对238U裂变截面的敏感性系数与它对238U平均裂变中子数的趋势基本一致，在快中子区出现峰值，这与238U容易发生裂变的能量范围一致，(n,γ)截面的敏感性系数在共振区有强烈的波动，反映了238U的共振峰对keff的影响。RMC的计算结果和MCNP6的吻合良好。

表3 总截面的敏感性系数Table 3 Sensitivity coefficients for total cross sections

图3 235U(a)和238U(b)的重要敏感性系数曲线Fig.3 Curves of some important sensitivity coefficients of 235U (a) and 238U (b)

4 结论与展望

本文讨论了敏感性系数的理论基础及反复裂变几率法的基本原理，基于自主堆用蒙特卡罗程序RMC，开发了连续能量蒙特卡罗计算中keff对核数据的敏感性分析功能。选用了3×3燃料栅格临界基准题，对RMC及MCNP6的计算结果进行了比较。RMC和MCNP6的keff偏差小于1 pcm，RMC计算得到的敏感性系数与MCNP6计算的比值基本在1左右，吻合良好。敏感性分析是不确定性分析的基础，本文工作为后续的不确定性分析打下了基础。下一步工作将结合协方差数据库，使用RMC进行keff对核数据的不确定性分析。

[1] ZWERMANN W, GALLNER L, KLEIN M, et al. XSUSA solution for the PWR Pincell burnup benchmark[C]∥Proceedings of the 6th Workshop on OECD Benchmark for Uncertainty Analysis in Best-Estimate Modeling for Design, Operation and Safety Analysis of LWRs (UAM-6). Karlsruhe, Germany: [s. n.], 2012.

[2] SCALE: A comprehensive modeling and simulation suite for nuclear safety analysis and design, Version 6.1, ORNL/TM-2005/39[R]. USA: Oak Ridge National Laboratory, 2011.

[3] KIEDROWSKI B C, BROWN F B. Comparison of the Monte Carlo adjoint-weighted and differential operator perturbation methods[R]. USA: Los Alamos National Laboratory, 2010.

[4] NAUCHI Y, KAMEYAMA T. Development of calculation technique for iterated fission probability and reactor kinetic parameters using continuous-energy Monte Carlo method[J]. J Nucl Sci Technol, 2010, 47(11): 977-990.

[5] REARDEN B T, PERFETTI C M, WILLIAMS M L, et al. SCALE sensitivity calculations using contributon theory[C]∥ Proceedings of Joint International Conference on Supercomputing in Nuclear Applications and Monte Carlo 2010 (SNA+MC2010). Tokyo, Japan: [s. n.], 2010.

[6] PERFETTI C M, REARDEN B T. Development of a SCALE tool for continuous-energy eigenvalue sensitivity coefficient calculations[C]∥Joint International Conference on Supercomputing in Nuclear Applications and Monte Carlo 2013 (SNA+MC 2013). Paris, France: [s. n.], 2013.

[7] PERFETTI C M. Advanced Monte Carlo methods for continuous-energy eigenvalue sensitivity coefficient calculation[D]. USA: University of Michigan, 2012.

[8] KIEDROWSKI B C, BROWN F B, WILSON P P H. Adjoint-weighted tallies fork-eigenvalue calculations with continuous-energy Monte Carlo[J]. Nuclear Science and Engineering, 2011, 168(3): 226-241.

[9] KIEDROWSKI B C, BROWN F B. Adjoint-basedk-eigenvalue sensitivity coefficients to nuclear data using continuous-energy Monte Carlo[J]. Nuclear Science and Engineering, 2012, 174: 227-244.

[10]SHIM H J, KIM C H. Adjoint sensitivity and uncertainty analyses in Monte Carlo forward calculations[J]. Journal of Nuclear Science and Technology, 2011, 5: 1 453-1 461.

[11]KIEDROWSKI B C. MCNP6.1k-eigenvalue sensitivity capability: A users guide, LA-UR-13-22251[R]. USA: LANL, 2013.

[12]SHIM H J, HAN B S, JUNG J S, et al. MCCARD: Monte Carlo code for advanced reactor design and analysis[J]. Nuclear Engineering and Technology, 2012, 44(2): 161-176.

[13]REARDEN B T. Perturbation theory eigenvalue sensitivity analysis with Monte Carlo techniques[J]. Nucl Sci Eng, 2004, 146: 367-382.

[14]HURWITZ H. Physical interpretation of the adjoint flux: iterated fission probability[M]∥Naval reactor physics handbook, Vol. Ⅰ. RADKOWSKY A. USA: Atomic Energy Commission, 1964: 864-869.

[15]WANG Kan, LI Zeguang, SHE Ding, et al. RMC: A Monte Carlo code for reactor core analysis[C]∥Joint International Conference on Supercomputing in Nuclear Applications and Monte Carlo 2013 (SNA+MC 2013). Paris, France: [s. n.], 2013.

[16]DALLE H M. Monte Carlo burnup simulation of the Takahama-3 benchmark experiment[C]∥2009 International Nuclear Atlantic Conference: INAC 2009. Brazil: [s. n.], 2009.

keffSensitivity Analysis to Nuclear Data with RMC Code

QIU Yi-shu, YU Jian-kai, LIANG Jin-gang, WANG Kan

(DepartmentofEngineeringPhysics,TsinghuaUniversity,Beijing100084,China)

Methods suitable for sensitivity analysis in continuous-energy Monte Carlo codes become a research hotspot in the field of reactor physics. In this work, the formulas of sensitivity coefficients of five different reaction types were established. Then, the theoretical basis and the algorithm of the iterated fission probability method which was used widely currently were discussed. Furthermore, two Monte Carlo codes, RMC and MCNP6, were used to compute eigenvalue sensitivity coefficients to nuclear data. The agreement between RMC and MCNP6 is well. The results indicate that RMC is capable to perform sensitivity analysis preliminarily.

sensitivity analysis; iterated fission probability method; continuous-energy; RMC code

2014-06-18;

2014-12-02

国家自然科学基金资助项目(11475098)

丘意书(1990—)，男，广东河源人，博士研究生，反应堆物理专业

TL32

A

1000-6931(2015)10-1821-07

10.7538/yzk.2015.49.10.1821