浅议以二次函数为背景与四边形相结合的存在性问题解题策略

袁熹旸

摘 要：二次函数是初中数学的重要内容，是数与形结合的典范，特别是以二次函数为背景与四边形相结合的存在性问题数学题，因其知识面广，技巧性强，区分度较高，有利于优秀人才的选拔，因此，备受中考命题组的青睐。

关键词：二次函数;特殊四边形;数学思想

以二次函数为背景与四边形相结合的存在性问题，对知识的迁移能力、灵活的运用能力和分析能力要求较高，因此，近几年成为全国各省、市中考压轴题.

一、与平行四边形相结合的存在性问题

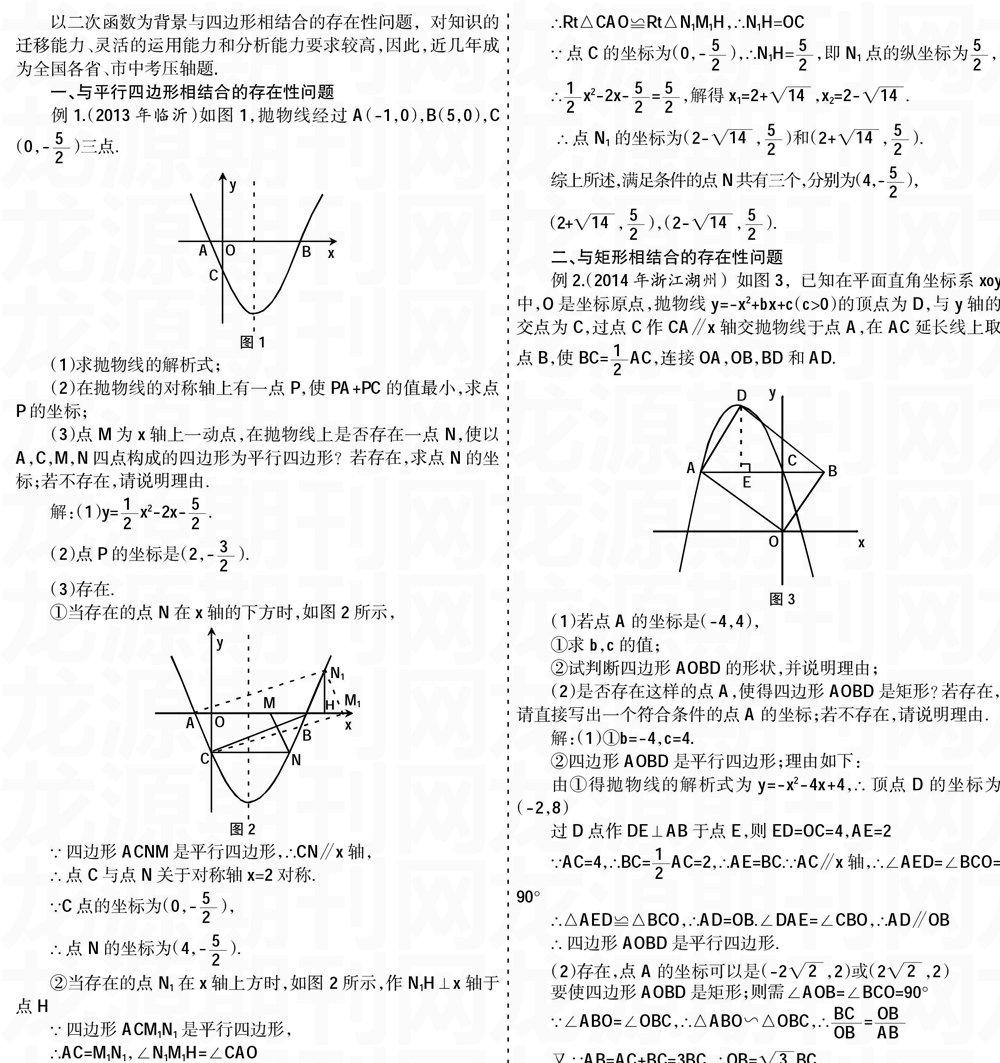
例1.（2013年临沂）如图1，抛物线经过A（-1，0），B（5，0），C（0，-）三点.

（1）求抛物线的解析式;

（2）在抛物线的对称轴上有一点P，使PA+PC的值最小，求点P的坐标;

（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以 A，C，M，N四点构成的四边形为平行四边形？若存在，求点N的坐标;若不存在，请说明理由.

解：（1）y=x2-2x-.

（2）点P的坐标是（2，-）.

（3）存在.

①当存在的点N在x轴的下方时，如图2所示，

∵四边形ACNM是平行四边形，∴CN∥x轴，

∴点C与点N关于对称轴x=2对称.

∵C点的坐标为（0，-），

∴点N的坐标为（4，-）.

②当存在的点N1在x轴上方时，如图2所示，作N1H⊥x轴于点H

∵四边形ACM1N1是平行四边形，

∴AC=M1N1，∠N1M1H=∠CAO

∴Rt△CAO≌Rt△N1M1H，∴N1H=OC

∵点C的坐标为（0，-），∴N1H=，即N1点的纵坐标为，

∴x2-2x-=，解得x1=2+，x2=2-.

∴点N1的坐标为（2-，）和（2+，）.

综上所述，满足条件的点N共有三个，分别为（4，-），

（2+，），（2-，）.

二、与矩形相结合的存在性问题

例2.（2014年浙江湖州）如图3，已知在平面直角坐标系xoy中，O是坐标原点，抛物线y=-x2+bx+c（c>0）的顶点为D，与y轴的交点为C，过点C作CA∥x轴交抛物线于点A，在AC延长线上取点B，使BC=AC，连接OA，OB，BD和AD.

（1）若点A的坐标是（-4，4），

①求b，c的值;

②试判断四边形AOBD的形状，并说明理由;

（2）是否存在这样的点A，使得四边形AOBD是矩形？若……