AN APPLICABLE APPROXIMATION METHOD AND ITS APPLICATION∗
Huaixin CAO(曹怀信)
Zhengli CHEN(陈峥立)
College of Mathematics and Information Science,Shaanxi Normal University,Xi'an 710062,China
Li LI(李莉)
School of Sciences,Xi'an Polytechnic University,Xi'an 710048,China
Baomin YU(余保良)
College of Mathematics and Information Science,Weinan Normal University,Weinan 714000,China
AN APPLICABLE APPROXIMATION METHOD AND ITS APPLICATION∗
Huaixin CAO(曹怀信)
Zhengli CHEN(陈峥立)
College of Mathematics and Information Science,Shaanxi Normal University,Xi'an 710062,China
E-mail:caohx@snnu.edu.cn;czl@snnu.edu.cn
Li LI(李莉)
School of Sciences,Xi'an Polytechnic University,Xi'an 710048,China
E-mail:lilian6263@163.com
Baomin YU(余保良)
College of Mathematics and Information Science,Weinan Normal University,Weinan 714000,China
E-mail:bmyuu@hotmail.com
In this work,by choosing an orthonormal basis for the Hilbert space L2[0,1],an approximation method for finding approximate solutions of the equation(I+K)x=y is proposed,called Haar wavelet approximation method(HWAM).To prove the applicability of the HWAM,a more general applicability theorem on an approximation method(AM)for an operator equation Ax=y is proved first.As an application,applicability of the HWAM is obtained.Furthermore,four steps to use the HWAM are listed and three numerical examples are given in order to illustrate the effectiveness of the method.
Hilbert space;applicability;Haar wavelet;approximation method;operator equation
2010 MR Subject Classification 47A58;65J10;45B05
1 Introduction
In recent years,many different basic functions were used to solving integral equations,such as orthonormal bases and wavelets.The orthogonal set of Haar functions[1]is the group of square waves with magnitude of±2i/2(i=0,1,2,···)and 0.Just these zeros make the Haar transform faster than other square functions such as Walsh function.Lynch and Reis[2]rationalized the Haar transform by deleting the irrational numbers and introducing the integral powers of two.This modification results in what is called the rationalized Haar(RH)transform.The RH transform preserves all the properties of the original Haar transform and can be efficiently implemented using digital pipline architecture.The corresponding functions areknown as RH functions[3].Maleknejad,et al.in[4-6]demonstrated applications of rationalized Haar wavelet for solving linear Fredholm integral equation of the second kind:
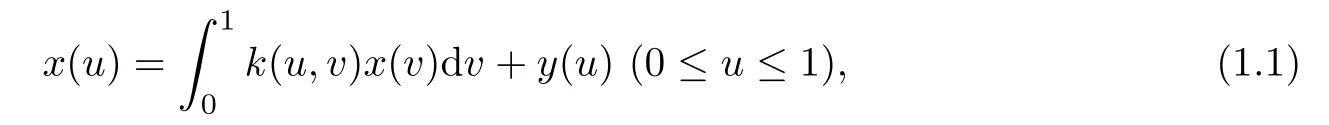
where x,y∈L2[0,1],k∈L2([0,1]×[0,1]),which is a special case of the following operator equation:

where K is a compact linear operator on the Hilbert space L2[0,1].
Due to the efficient applications of wavelets,some interesting topics were discussed recently in[7-10].In this work,by choosing an orthonormal basis for the Hilbert space L2[0,1],an approximation method will be proposed,called Haar wavelet approximation method(HWAM). To prove the applicability of the HWAM,we will prove a more general applicability theorem(Theorem 2.5,below)on an approximation method(AM)for an operator equation Ax=y.As an application of Theorem 2.5,we will obtain an applicable AM for equation(1.2)(Theorem 3.1),which is just HWAM.Also,steps to use the HWAM will be listed and three numerical examples should be given.
2 Approximation Methods
Let X be a Banach space over the complex field C and B(X)the unital Banach algebra of all bounded linear operators on X.Given a bounded linear operator A on X and a vector y in X,consider the operator equation

For the approximate solution of this equation,we choose appropriate closed subspaces Xn(n=1,2,···)in which the approximate solutions xnof(2.1)will be sought.We also assume that for each n there exists a projection Pnof X onto Xn,i.e.,a bounded linear operator from X onto Xnsuch that
Then let us choose bounded linear operators An:Xn→ Xn(n=1,2,···)and consider in place of(2.1)the equations

whose solutions xnwill be sought in Xn.With these assumptions and notations,let us recall the concept of approximation method for an operator A∈B(X)given in[11].
Definition 2.1 A sequence{An}∞n=1with An∈B(Xn)for all n is called an approximation method for A∈B(X)if the sequence{AnPn}∞n=1converges strongly to A,i.e.,
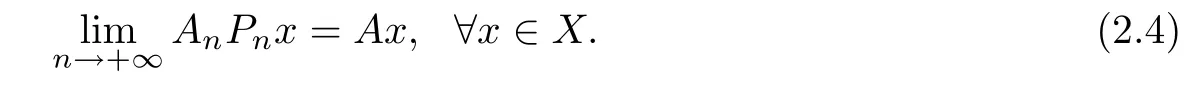
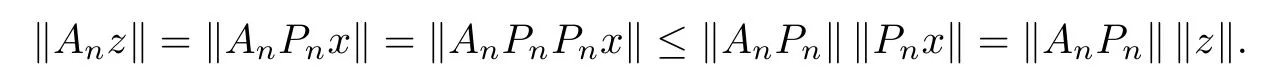
Definition 2.3 An approximation method{An}∞n=1for A is said to be applicable if there exists an n0such that for every n≥n0and each y∈X,equation(2.3)has a unique solution xnin Xnand the sequence{xn}∞n=1converges in norm to a solution x of equation(2.1).
Remark 2.4 If A∈B(X)has an applicable approximation method{An}∞n=1,then it must be onto.Moreover,next theorem shows that A is also injective and then invertible.
Theorem 2.5 Suppose that{An}∞n=1is an approximation method for A.Then{An}∞n=1is applicable for A if and only if it is stable,i.e.,there exists an n0such that Anis invertible for all n≥n0with
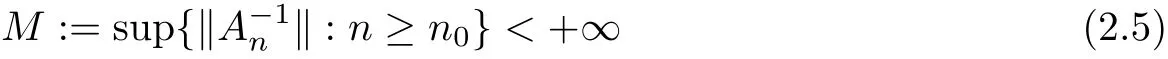
and A is injective.

On the other hand,for all x∈X,we compute that
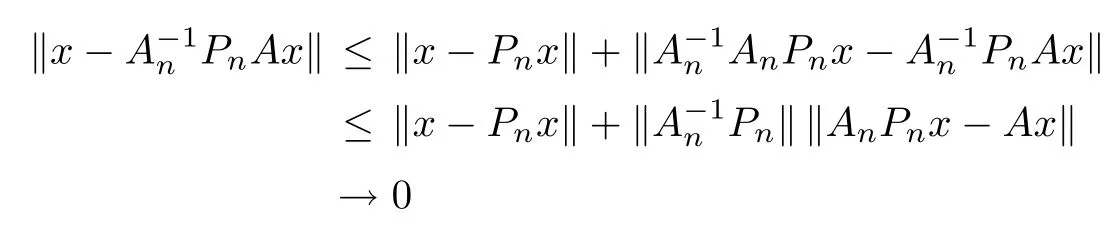
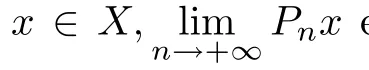
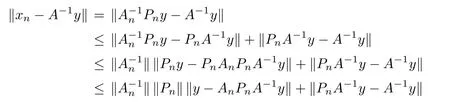
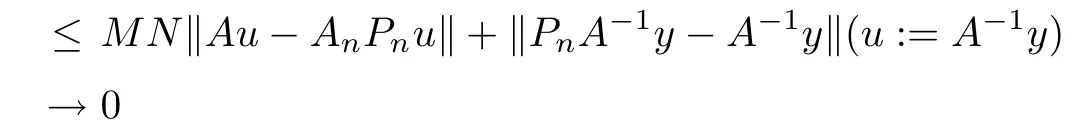
Corollary 2.6 Let X be a Hilbert space over C with an orthonormal basis{en}∞n=0,Pnthe orthogonal projection of X onto Xn:=span{e0,e1,e2,···,en}and K ∈B(X)be a compact operator with-1/∈σ(K).Put An=Pn(I+K)|Xn,then the sequence{An}∞n=0is an applicable approximation method for the operator A=I+K.
Proof Clearly,for every x∈X,we have Pnx→x in norm as n→+∞.Sinceis an approximation method for A=I+K.Since-1/∈σ(K),A∈B(X)is invertible. It follows from[11,Corollary 1.25]that there exists n0∈N such that
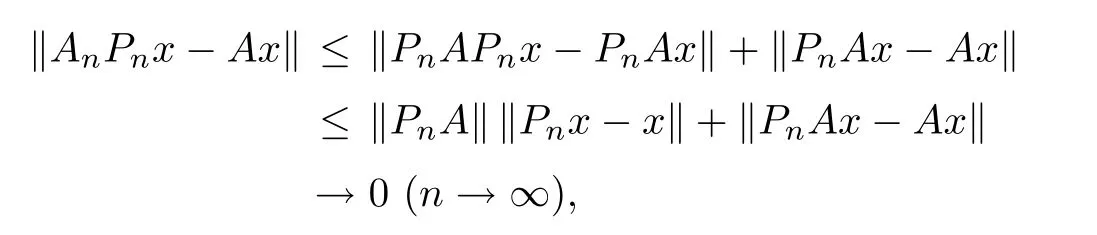
When n≥n0,for every z∈Xn,there exists an x∈X such that Pnx=z.Thus,
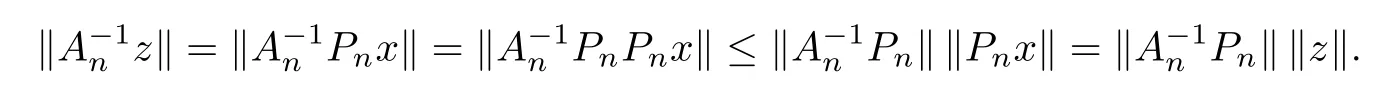
3 Haar Wavelet Approximation Method
For a compact operator K in B(L2[0,1]),we consider the following equation

where y∈L2[0,1]is arbitrarily given,and x is to be found.
The equation is uniquely solvable,i.e.,for each y∈L2[0,1]there exists one and only one solution x∈L2[0,1]of(3.1),if and only if the operator A=I+K is invertible,i.e.,-1/∈σ(K). Thus,we assume that-1/∈σ(K).To find the approximate solutions of(3.1),let us use the Harr wavelet approximation method.
For the Haar orthogonal wavelet
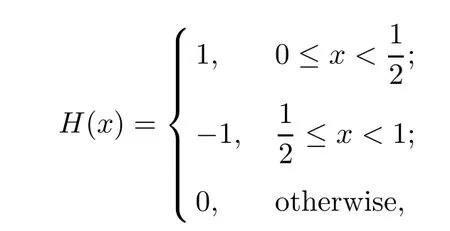
and Ω=[0,1],we have
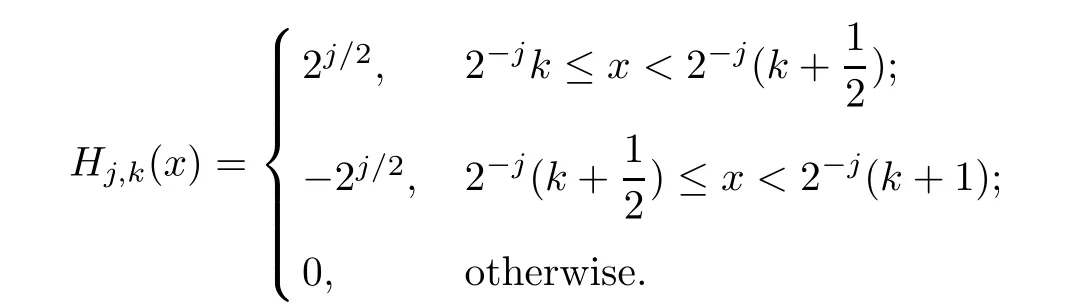
Put
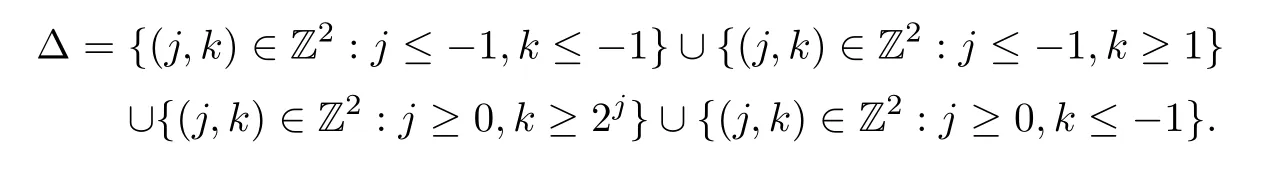
Then when(j,k)∈∆,we have Hj,k(x)=0 a.e.on[0,1],and
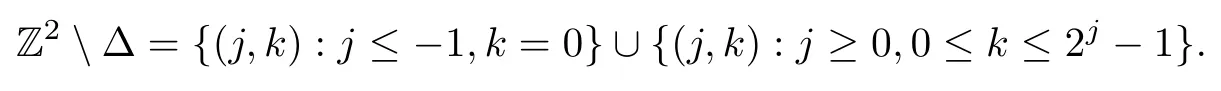
It is well-known that the sequence ε(H):={Hj,k}j,k∈Zis an orthonormal basis for L2(R). Let ϕ=χ[0,1).For every function f∈L2[0,1],we define f(u)=0 if u∈R[0,1].Then as an element of L2(R),we have
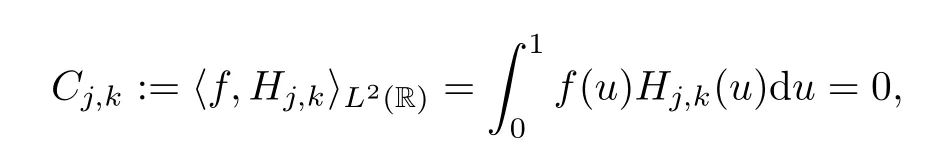
whenever(j,k)∈∆,and when j≤-1,

When u∈[0,1),we have
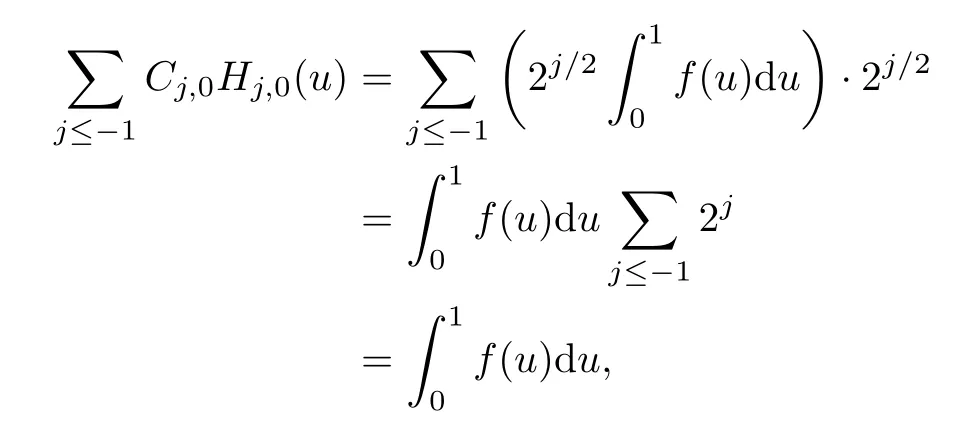
Thus,as elements of L2[0,1],we obtain that

with norm convergence.This shows that the sequence
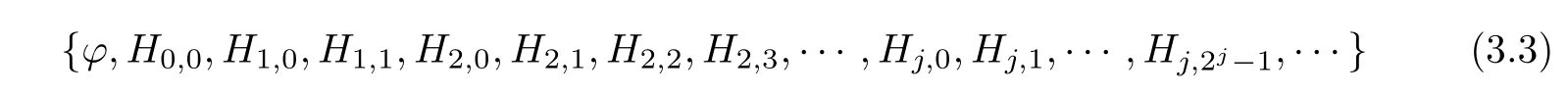
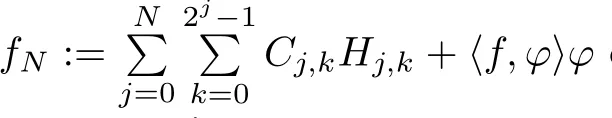
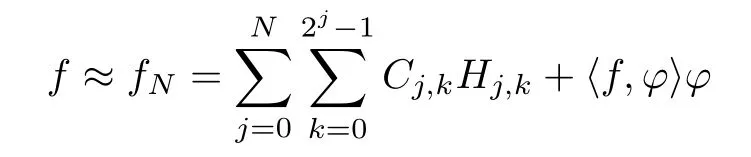
for sufficiently large N.
Let Pjbe the orthogonal projection of L2[0,1]onto
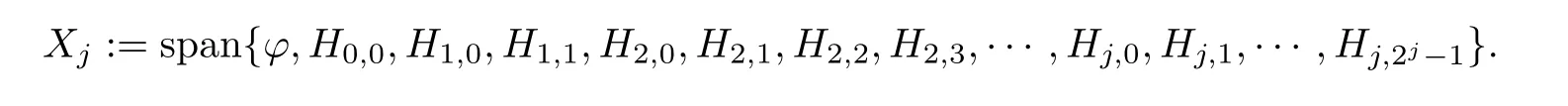
Then the approximate equations of(3.1)are as follows.
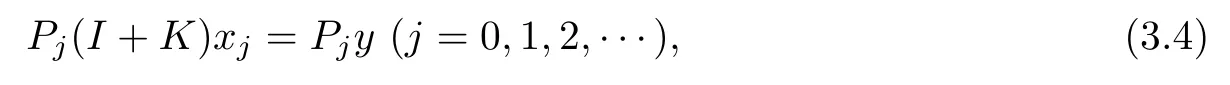
where y∈L2[0,1]is arbitrarily given,and xjis to be found in Xj.
With these notations,we have the following applicability theorem.
Theorem 3.1 If-1/∈σ(K),then the sequenceis an applicable approximation method for the operator A=I+K.Explicitly,there exists a j0such that for every j≥j0and each y∈L2([0,1]),equation(3.4)has a unique solution xjin Xjand that the sequenceconverges in norm to a solution x of equation(3.1).
Proof Put Aj=Pj(I+K)|Xj(j=0,1,2,···)and denote basis(3.3)by e0,e1,···,en,···.Clearly,Hj,2j-1=e2j+1-1and let Qnbe the orthogonal projection of L2[0,1]onto the space
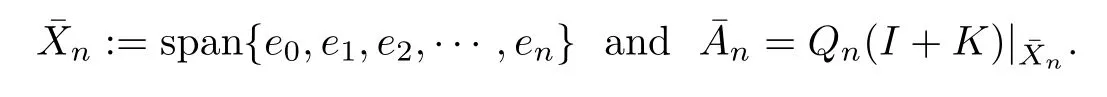
Then by Corollary 2.6 we know that when-1/∈σ(K),the sequenceis an applicable approximation method for I+K.Clearly,andfor all j.Hence,as a subsequence ofis also an applicable approximation method for I+K.
Now,let us assume that-1/∈σ(K)and use the notations described before Theorem 3.1.For each fixed integer j and each fixed vector y∈L2[0,1],we see that equation(3.4)is equivalent to the following linear system of 2j+1equations:
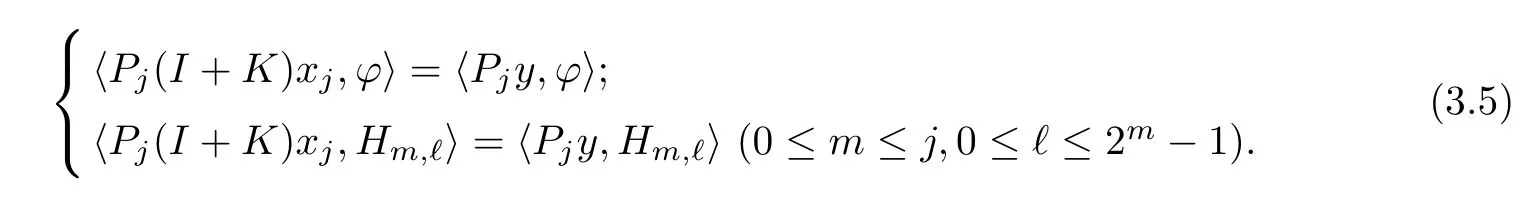
Since xj∈Xj,we can write
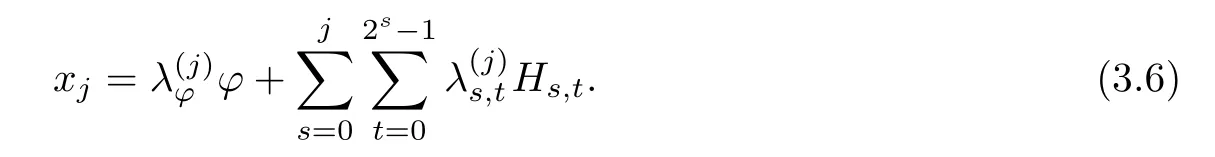
By letting
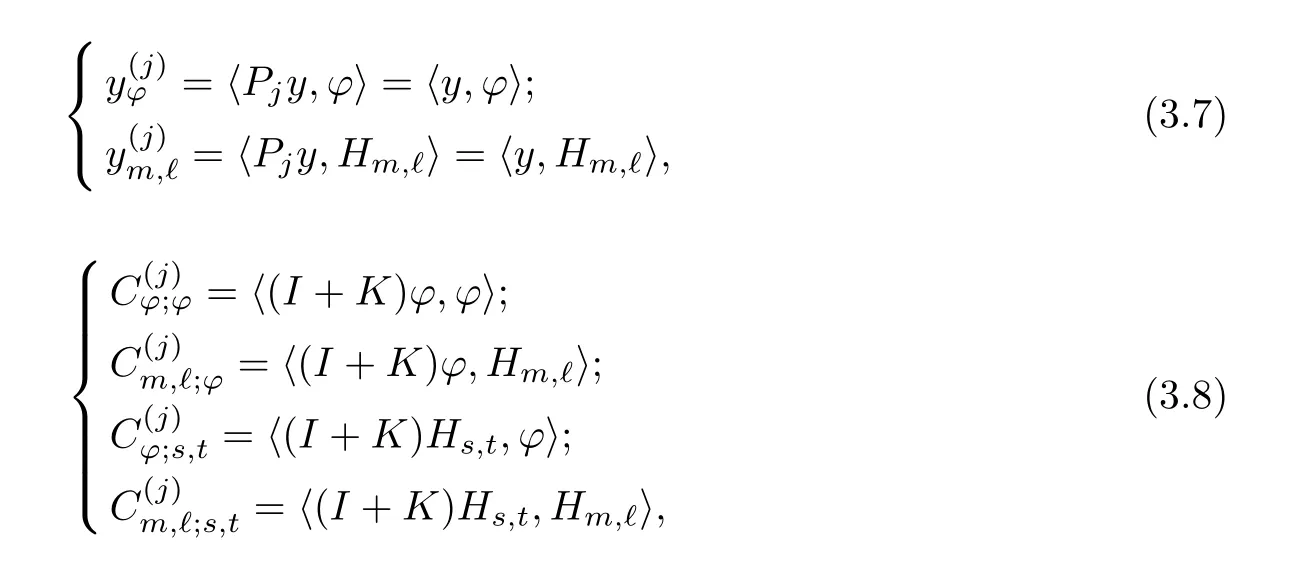
where 0≤m≤j,0≤ℓ≤2m-1 and 0≤s≤j,0≤t≤2s-1,equation(3.5)becomes
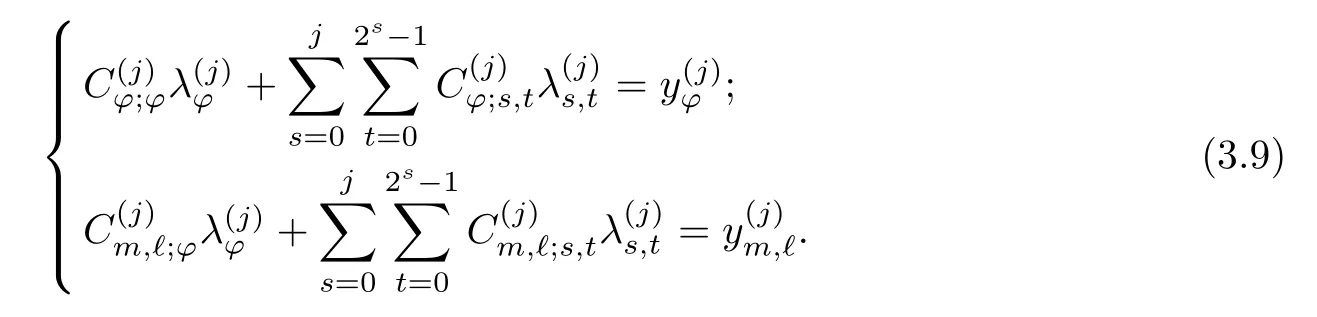
Let D(j)denote the following 2j+1-1 by 2j+1-1 matrix:
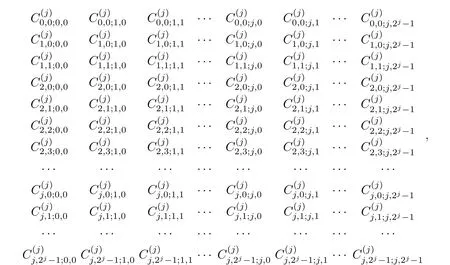
and put
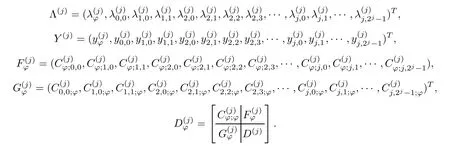
Then equation(3.9)can be written as

From Theorem 3.1,we can choose a positive integer j0such that the operator Pj(I+K)|Xjis invertible and then the corresponding matrix D(j)ϕis invertible for all j≥j0.In this case,the solution of(3.10)is given by

Furthermore,when Λ(j)is given by(3.11),sequence(3.6)converges to some x as j→∞such that Ax=y.Equivalently,the error ej(u):=x(u)-xj(u)converges in norm to zero as j→∞.
From the discussion above,we obtain an applicable approximate method to find approximate solutions of equation(3.1)with the following steps:
Step 1 For a given function y∈L2[0,1]and an large j,use(3.7)to find the column vector Y(j);
Step 2 Use(3.8)to find the coefficient matrix D(j)ϕ;
Step 3 Use(3.11)to get the coefficient vector Λ(j);
Step 4 Use(3.6)to get the approximate solution xj.
We call this method the Haar wavelet approximation method(HWAM).
4 Examples
As an example,let us consider the Fredholm integral equation of the second kind[4]:
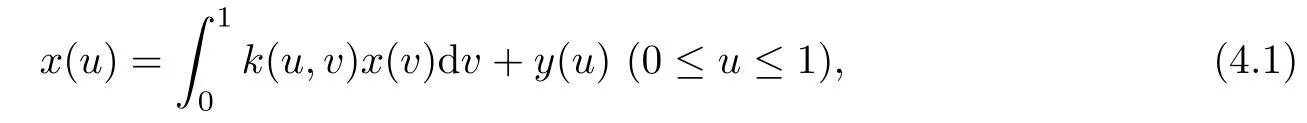
where y∈L2[0,1],k∈L2([0,1]×[0,1])are given and x∈L2[0,1]is unknown and to be found.
To find an approximate solution,let us define
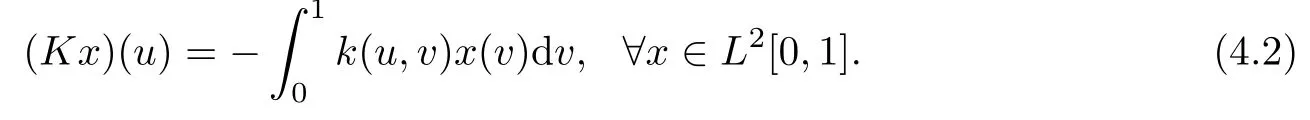
Then equation(4.1)becomes the following operator equation:

Clearly,the operator K:L2[0,1]→L2[0,1]is linear and compact satisfying‖K‖≤‖k‖2.To use Theorem 3.1,let us assume that
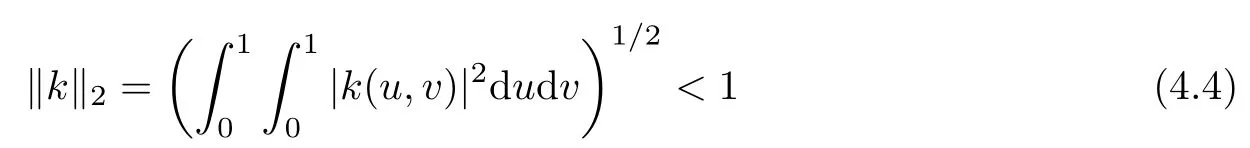
and so‖K‖<1.This implies that-1/∈σ(K).Thus,for a given y∈L2[0,1],there exists a positive integer j0such that the sequencedefined by(3.6)and(3.11)converges to the unique solution x of(4.1).
From(3.7),we know that
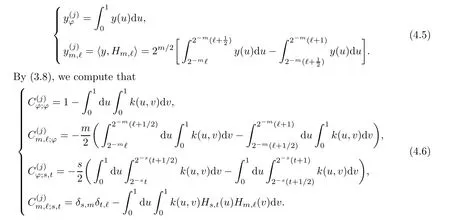
Example 4.1 Let
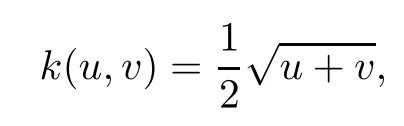
and
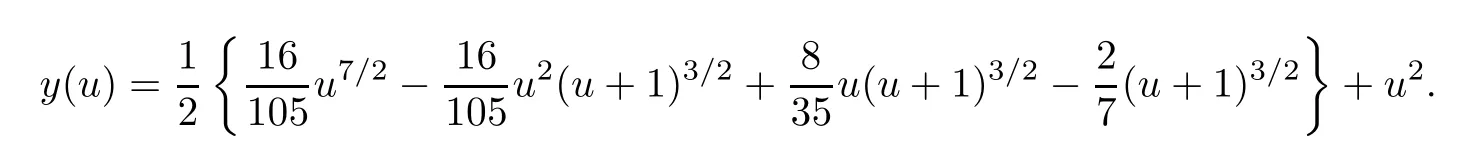
Then equation(4.1)has the unique exact solution x(u)=u2.Sincefor all u,v∈(0,1),‖k‖2<1 and so the sequence{xj}given by(3.6)and(3.11)converges to the unique exact solution x of(4.1)as j→∞.See Table 1 and Fig.1(a).
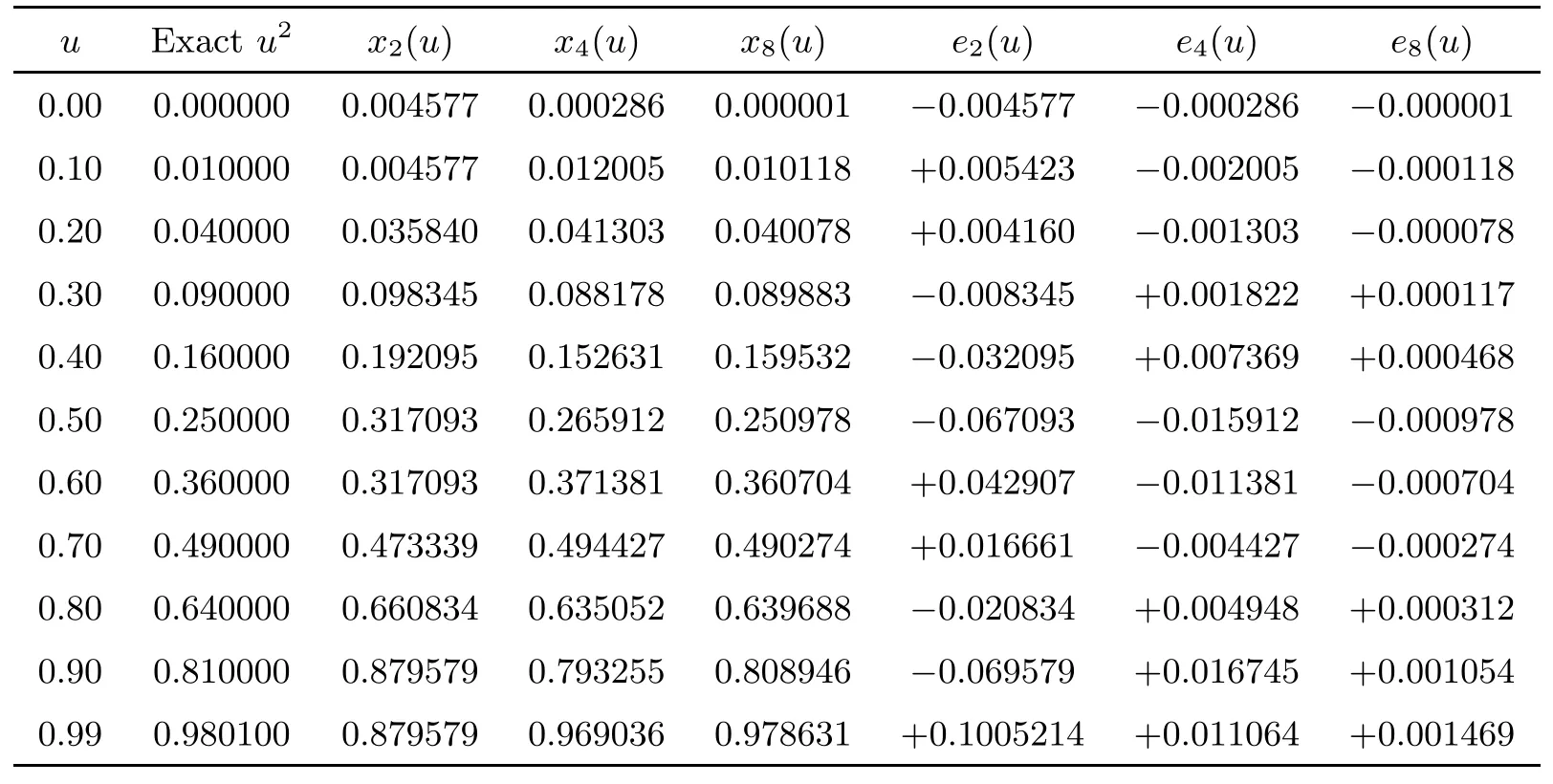
Table 1 Numerical results of Example 4.1 with different j
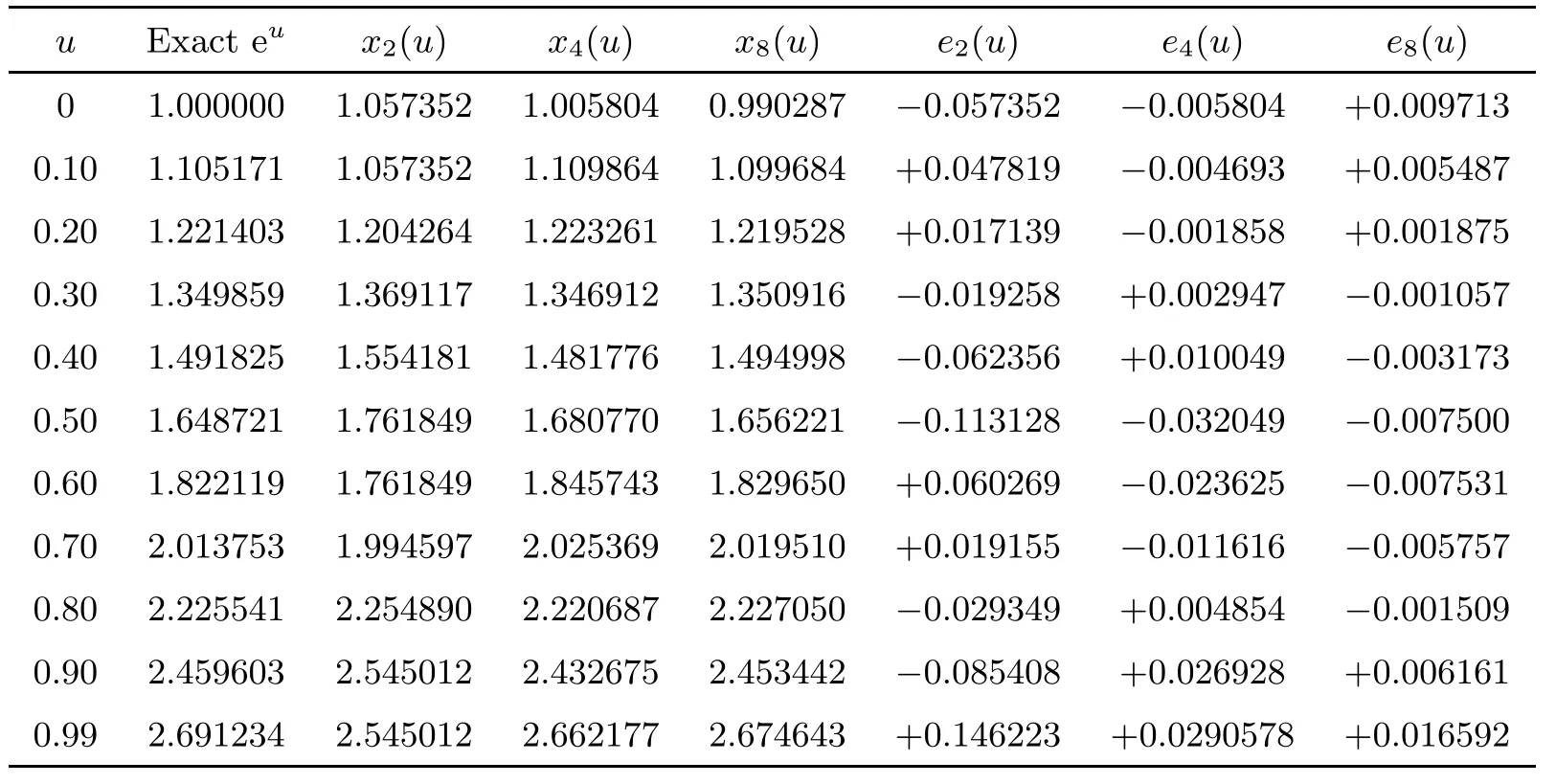
Table 2 Numerical results of Example 4.2 with different j
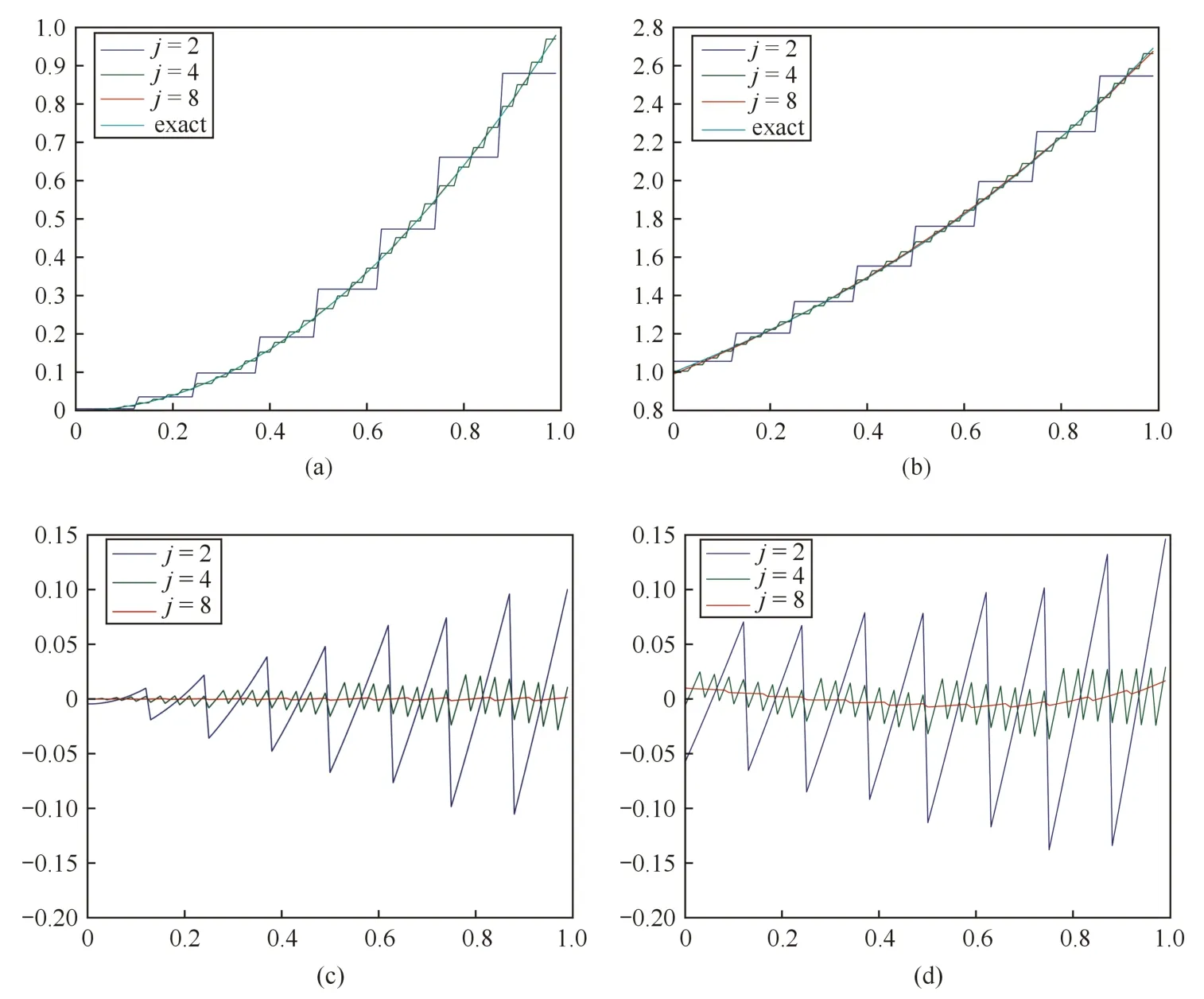
Fig.1 Results of Example 4.1 and Example 4.2 with j=2,4,8,respectively.From this figure,we see that the curves for the case that j=8 and the exact solution coincide almost everywhere.
Example 4.2 Consider the equation
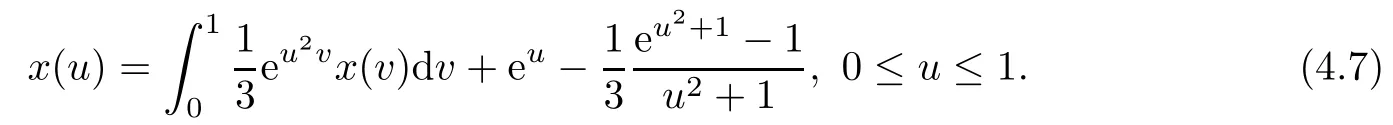
It is easy to check that the function x(u)=euis the exact solution of(4.7).Let

Then(4.7)becomes(4.1).Since 0<k(u,v)≤e3<1 for all u,v∈(0,1),‖k‖2<1 and so the sequence{xj}given by(3.6)and(3.11)converges to the unique exact solution x of(4.1)as j→∞.See Table 2 and Fig.1(b).
Example 4.3 Consider the equation
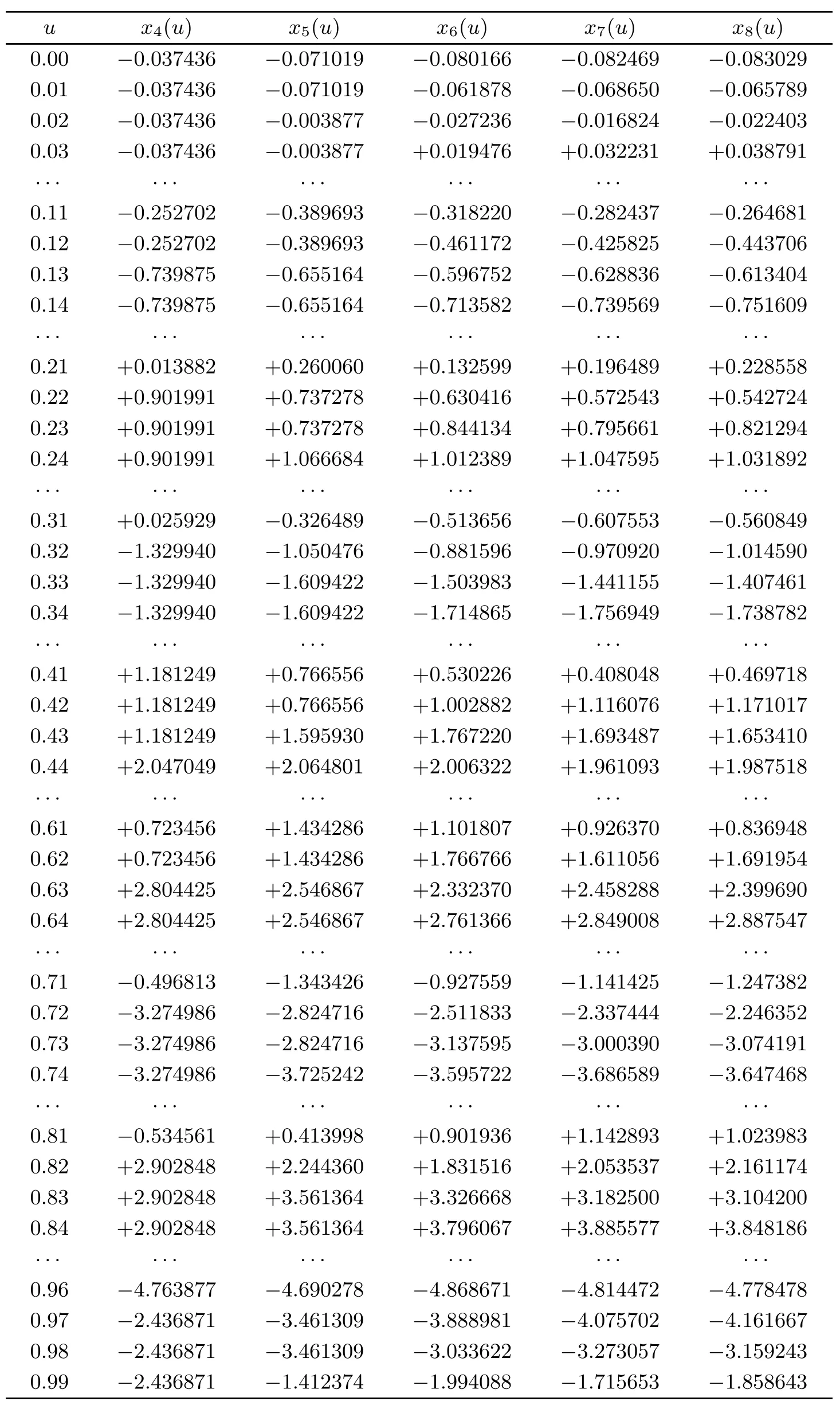
Table 3 Numerical results of Example 4.1 with different j,where dj(u)=xj(u)-xj-1(u)
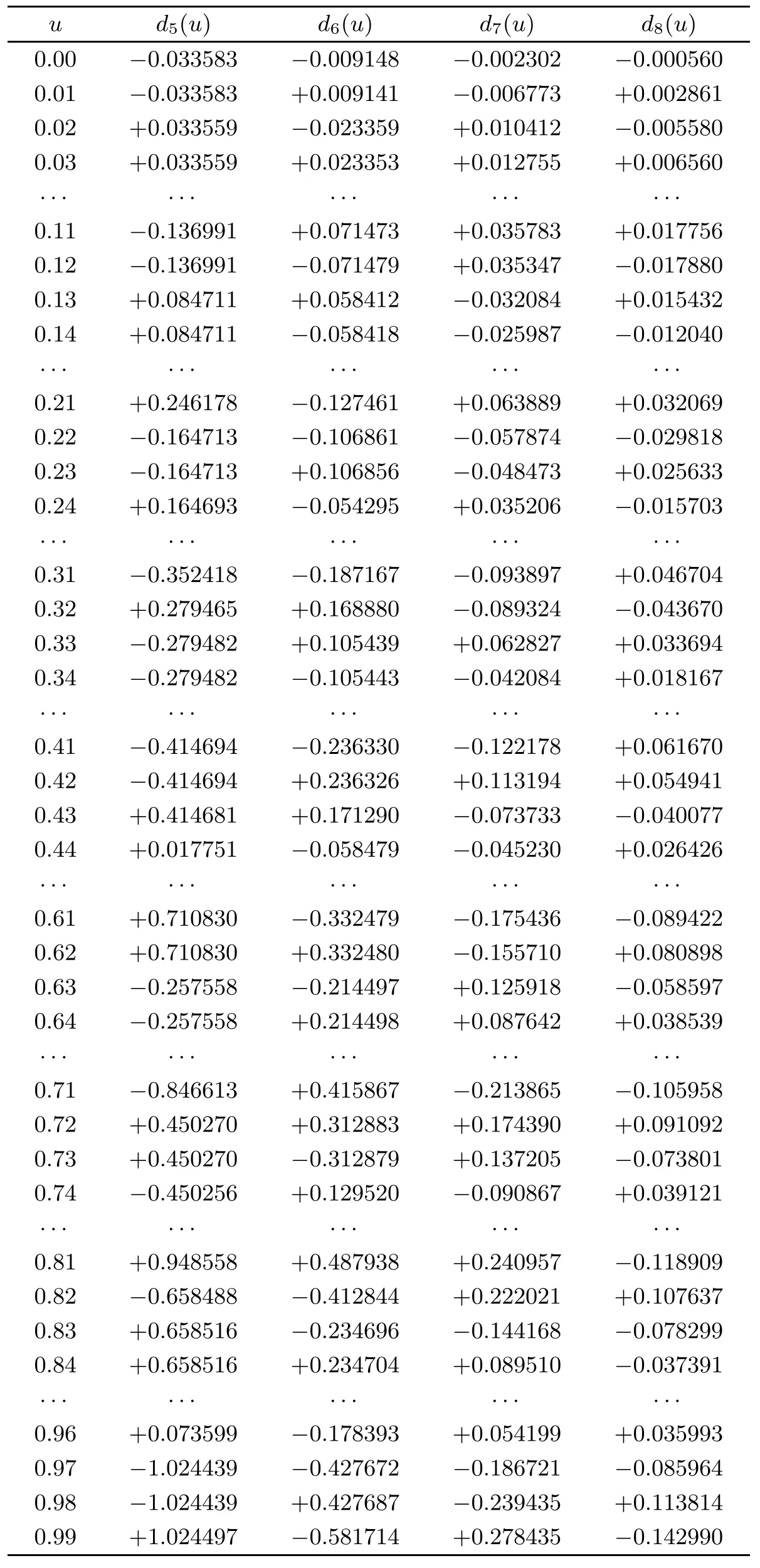
Continuation of Table 3
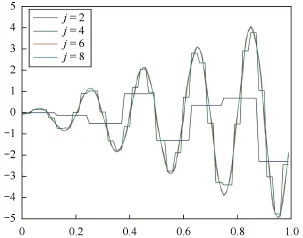
Fig.2 Results of Example 4.3 with j=2,4,6,8.From this figure,we see that the curves for j=6 and j=8 coincide almost everywhere.
5 Conclusion
In this paper,we present an approximation method for finding approximate solutions of the equation(I+K)x=y by choosing an orthonormal basis for the Hilbert space L2[0,1],called Haar wavelet approximation method(HWAM).To prove the applicability of the HWAM,a more general applicability theorem on an approximation method(AM)for an operator equation Ax=y has been established.Furthermore,the four steps to use the HWAM have been listed. The employed three examples illustrate numerically the applicability of the method.
It is important to point out that when‖K‖<1,the operator I+K in equation(4.3)is invertible and has the inverse:
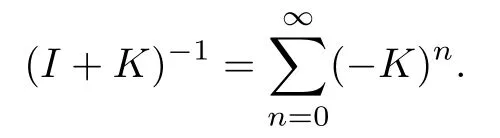
In this case,for each y∈L2[0,1],equation(4.3)has a unique solution
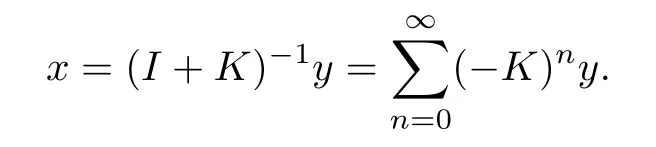
[1]Lynch R T,Reis J J.Haar transform image coding.Proceedings of the National Telecommunications Conference,Dallas,TX,1976,44.3-1-44.3-5
[2]Reis J J,Lynch R T,Butman J.Adaptive Haar transform video bandwidth reduction system for RPVAs. Proceedings of Annual Meeting of Society of Photo-Optic Institute of Engineering(SPIE),San Dieago,CA,1976:24-35
[3]Ohkita M,Kobayashi Y.An application of rationalized Haar functions to solution of linear differential equations.IEEE Trans Circuit Syst,1986,9:853-862
[4]Maleknejad K,Mirzaee F.Using Rationalized Haar wavelet for solving linear integral equations.Appl Math Comput,2005,160:579-587
[5]Maleknejad K,Mirzaee F.Numerical solution of linear Fredholm integral equations system by rationalized Haar functions method.Int J Comput Math,2003,8:1397-1405
[6]Rabbani M,Maleknejad K,Aghazadeh N,Mollapourasl R.Computational projection methods for solving Fredholm integral equation.Appl Math Comput,2007,191:140-143
[7]Li Y F,Yang S Z.A class of multiwavelets and projected frames from two-direction wavelets.Acta Math Sci,2014,34B(2):285-300
[8]Yang Q X.Characterization of multiplier spaces with Daubechies wavelets.Acta Math Sci,2012,32B(6): 2315-2321
[9]Yang S Z,Shen Y F,Li Y F.A class of compactly supported orthogonal symmetric complex wavelets with dilation factor 3.Acta Math Sci,2012,32B(4):1415-1425
[10]Lu D Y,Li D F.A characterization of orthonormal wavelet frames in Sobolev spaces.Acta Math Sci,2011,31B(4):1475-1488
[11]Hagen R,Roch S,Silbermann B.C∗-Algebras and Numberical Analysis.New York:Marcel Dekker Inc,2001
∗Received July 3,2013;revised march 6,2015.This work was partial support by the NSFC(11371012,11401359,11471200),the FRF for the Central Universities(GK201301007),and the NSRP of Shaanxi Province(2014JQ1010).
 Acta Mathematica Scientia(English Series)2015年5期
Acta Mathematica Scientia(English Series)2015年5期
- Acta Mathematica Scientia(English Series)的其它文章
- ASYMPTOTIC BEHAVIOR OF GLOBAL SMOOTH SOLUTIONS FOR BIPOLAR COMPRESSIBLE NAVIER-STOKES-MAXWELL SYSTEM FROM PLASMAS∗
- ON SOLVABILITY OF A BOUNDARY VALUE PROBLEM FOR THE POISSON EQUATION WITH A NONLOCAL BOUNDARY OPERATOR∗
- GENERAL DECAY OF SOLUTIONS FOR A VISCOELASTIC EQUATION WITH BALAKRISHNAN-TAYLOR DAMPING AND NONLINEAR BOUNDARY DAMPING-SOURCE INTERACTIONS∗
- Lp-CONTINUITY OF NONCOMMUTATIVE CONDITIONAL EXPECTATIONS∗
- CONTROLLABILITY AND OPTIMALITY OF LINEAR TIME-INVARIANT NEUTRAL CONTROL SYSTEMS WITH DIFFERENT FRACTIONAL ORDERS∗
- A MATHEMATICAL MODEL OF ENTERPRISE COMPETITIVE ABILITY AND PERFORMANCE THROUGH EMDEN-FOWLER EQUATION FOR SOME ENTERPRISES∗
