（2+1）维扩展Zakharov-Kuznetsov方程的对称、约化和精确解

李 康，刘希强

（聊城大学数学科学学院，山东，聊城 252059）

0 引言

近些年来，为了求解非线性数学物理方程精确解，提出了大量的行之有效的求解方法，如Jacobi椭圆函数法、齐次平衡法、G’/G展开法、Hirota双线性方法、双曲函数法等等[1-7]。本文考虑方程

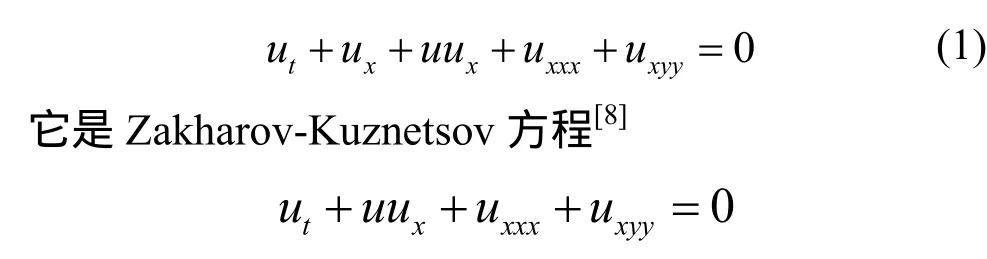
的扩展，Zakharov-Kuznetsov方程(简称ZK方程)是著名的KdV方程在二维空间的推广形式，它是应用渐进多尺度技术在磁场中发现的一种磁等离子波，在物理领域有着广泛的应用。长期以来许多学者对有关它们的课题进行了广泛的研究[9-11]。

本文借助李群理论求出方程(1)的对称，然后进行约化并利用Riccati辅助方程[12]以及雅可比椭圆函数法等求出方程(1)的某些精确解。

1 方程(1)的对称

首先，考虑一个单参数李群的无穷小变换：

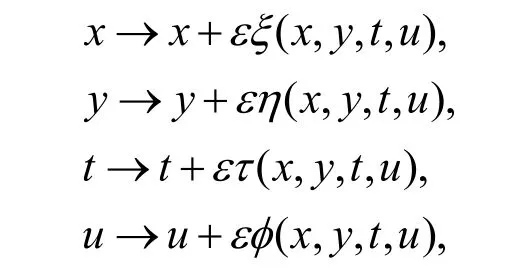
其中ε是无穷小参数。上述变换群的向量场可以表示如下：

其中,,ξητ和φ是待定的系数函数。由李群理论，得到三阶延拓：

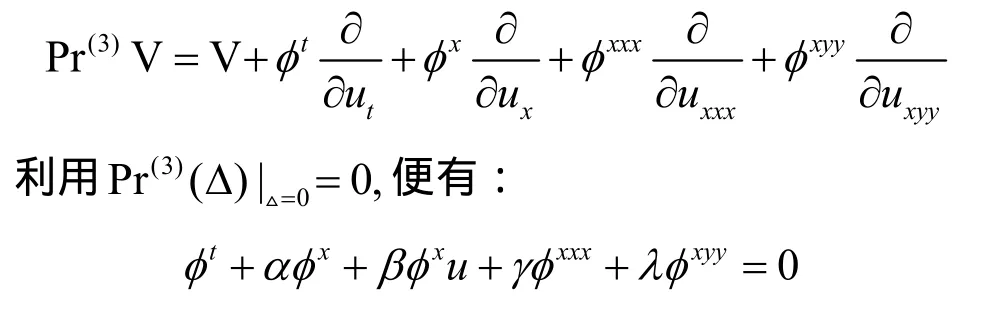
其中 Δ = ut+ α ux+ β uux+ γ uxxx+ λ uxyy。利用李群法，可得：

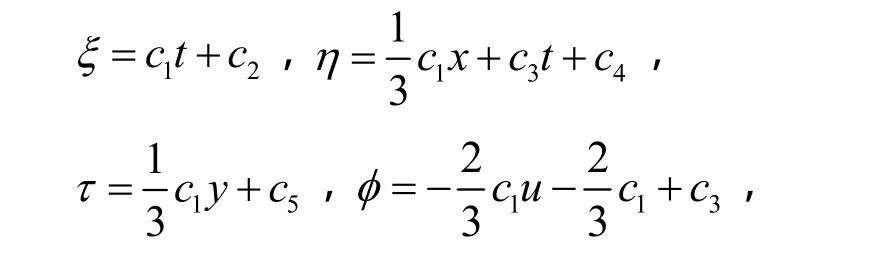
其中 ci(i = 1 ,2,3,4,5)是任意常数。由上述结果得到方程(1)的不变群生成元：

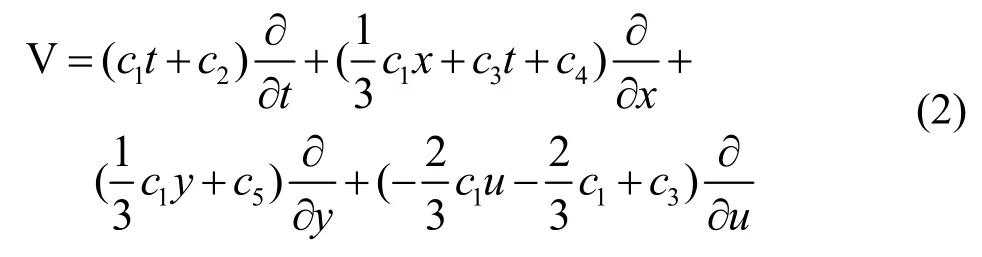
不变群的全体生成元构成一个五维李代数，并有下列一组基：

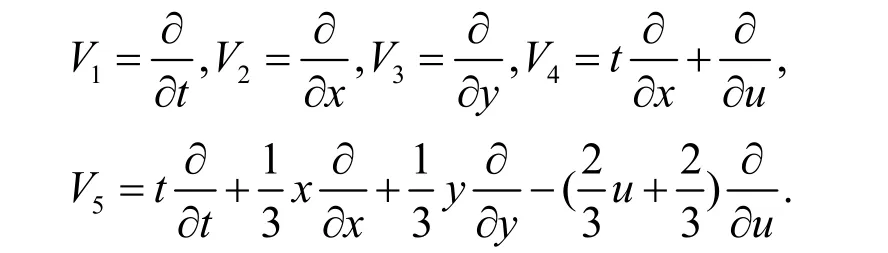
利用Vi(i=1,…,5)得到方程(1)的单参数群gi(i=1,…,5)如下：

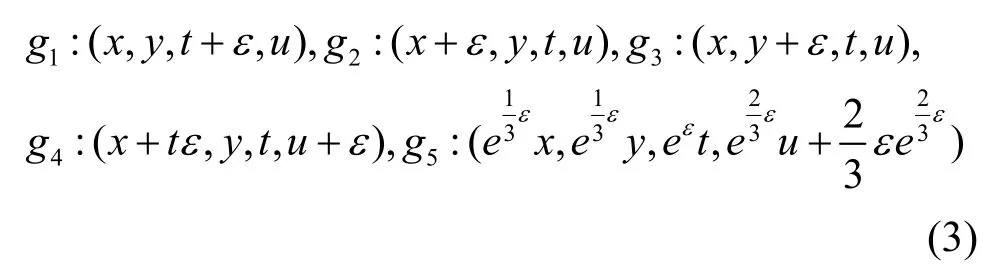
由(3)中的单参数群 gi(i=1,…,5)可以得到方程(1)的解的表达式为：

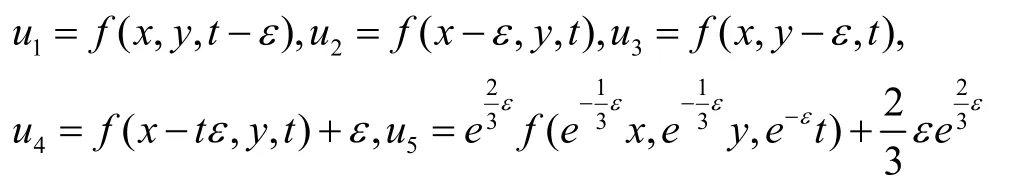
其中ε是参数，f是方程(1)的任意已知解。由(2)可知方程(1)的对称为

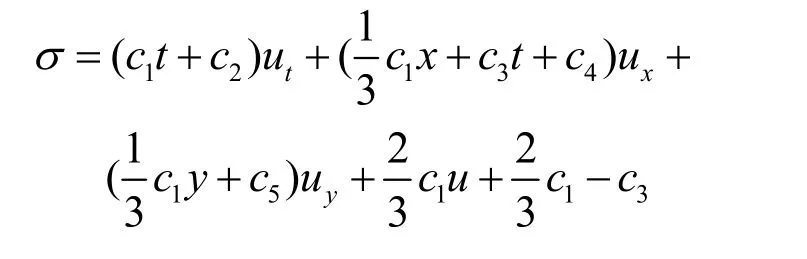
2 方程(1)的相似约化和精确解

为了求出方程(1)的相似约化和精确解，必须解相应的特征方程组，方程(1)对应的对称的特征方程组为

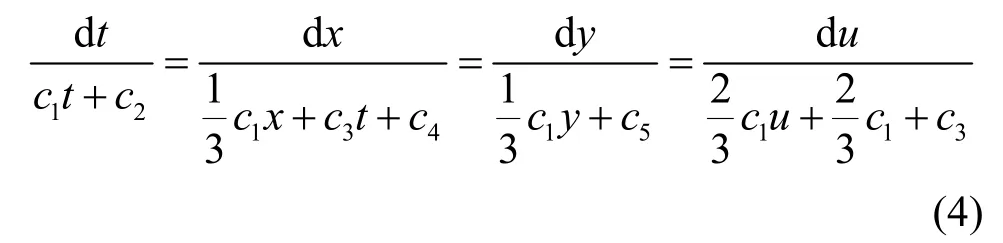
通过解特征方程组(4)得到了方程(1)的不变量和对应的相似约化方程。

表1 方程(1)的经典相似约化Table 1 The classic similarity reduction of equation (1)

情况1

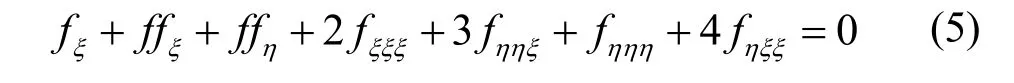
下面利用 G '/ G展开方法求解方程(5)。做行波变换，将 f ( ξ ,η) = f( ζ ),ζ = k ξ + l η ，代入到(5)式中得到

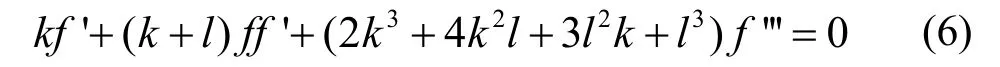
通过平衡(6)式中的最高阶导数项和非线性项，可得(6)式应有满足下式的解

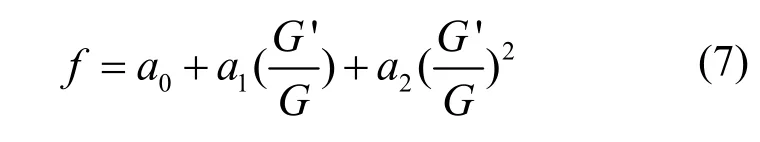
其中 ai(i=0,1,2)为待定常数， G =G(ξ)满足二阶线性常微分方程

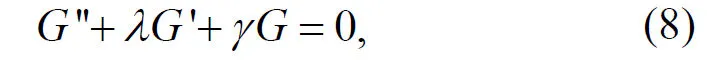
将(7)式代入(6)式，并利用(8)式，令（ '/G G）的同次幂项的系数为零，可得

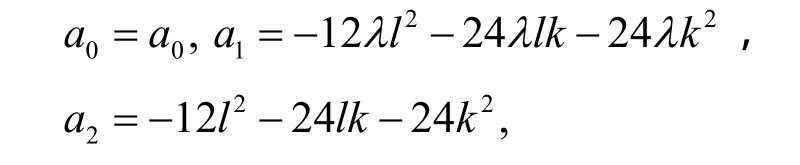
其中 λ ,γ, k ,l,a0是任意常数，因此(7)式可表示为

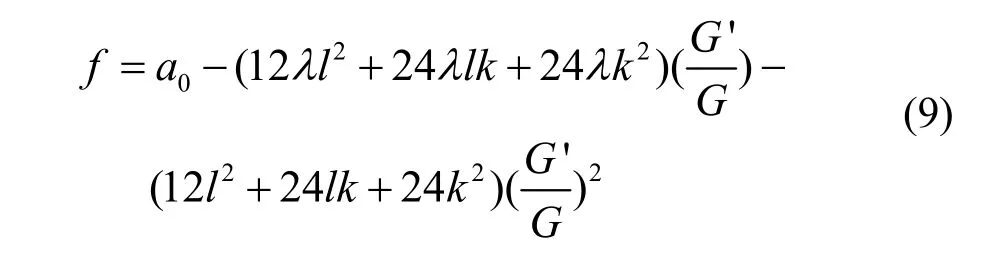
将(8)式的解代入(9)式可得方程(1)的三种形式的行波解：

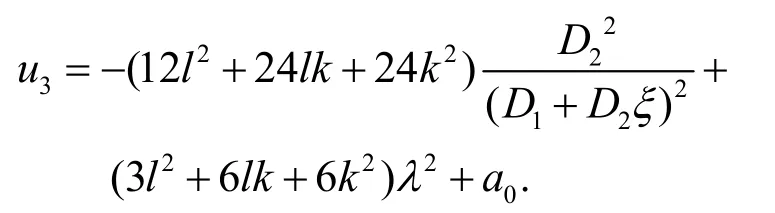
情况2 同情况1类似，省略。

情况3

利用Riccati辅助方程求解方程(11)。通过平衡(11)式中的最高阶导数项和非线性项，可得(11)式应有满足下式的解

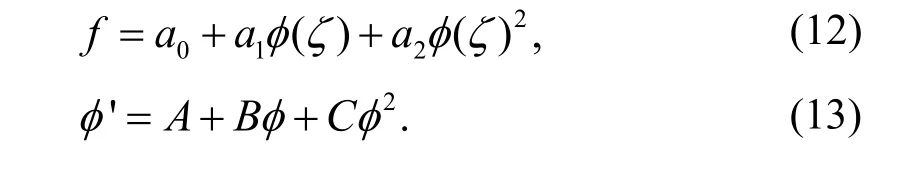
其中ai(i=0,1,2)为待定常数，φ满足(13)式Riccati方程。将(12)(13)式代入(11)式，令v的同次幂项的系数等于零，可得

则原方程的解为

则原方程的解为

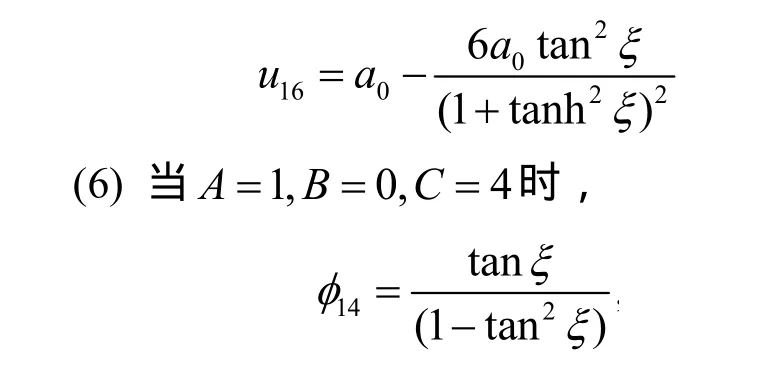
则原方程的解为

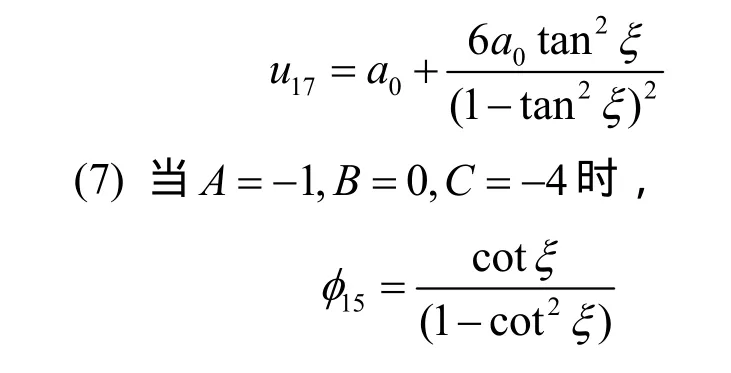
则原方程的解为

则原方程的解为

为了得到方程(14)更多的解，这里选用雅可比椭 圆 函 数 求 解 。 做 行 波 变 换 f( ξ ,η) = f(ζ)，ζ=kξ +lη得到

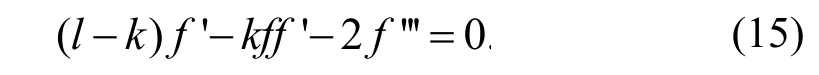
设方程组(15)有如下形式的解

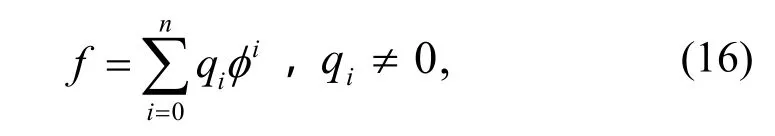
平衡(15)式中的 f′′与 f 'f得到 n + 3 = 2 n +1，即有n=2。由(16)式得

把(17)式和(18)式代入(15)式，令φ相同次数的系数为0，得到相关的代数方程组，解之得

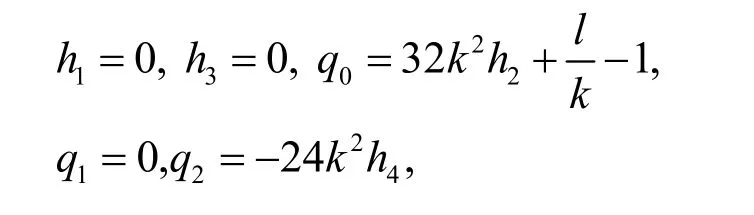
如果能求出情况7与情况8中的解，同样也可以得到方程(1)的新的精确解。

3 结论

本文利用李群方法求出了方程(1)的对称，然后进行约化得到了几种约化方程，再结合Riccati辅助方程及雅可比椭圆函数法，求出了方程(1)的一些精确解。应用这种方法可求出许多非线性偏微分方程组的精确解，表明这种方法是实用有效的。

[1] Dai C Q, Zhang J F. Jacobin elliptic function method for nonlinear differential-difference equations[J]. Chaos,Solitons &fractals,2006,27(4):1042-1047.

[2] Fan E, Zhang J. Applications of the Jacobi elliptic function method to special-type nonlinear equations[J].Phys Lett,A 2002,305(6):383-392.

[3] 辛祥鹏,张琳琳.ZK-MEW 方程的对称约化、精确解及守恒律[J].井冈山大学学报:自然科学版,2010,31(4):9-14.

[4] 田贵辰，刘希强.长水波近似方程组的新精确解[J].数学的实践与认识,2005,35(3):105-110.

[5] 王岗伟,刘希强,张颖元.变系数mKdV方程的精确解[J].井冈山大学学报:自然科学版,2012,33(5):1-5.

[6] Hirota R, Satsuma J. A variety of nonlinear network equations generated from the Bäcklund transformation for the Toda lattice[J]. Progress of Theoretical Physics Supplement, 1976, 59: 64-100.

[7] Liu H, Li J, Chen F. Exact periodic wave solutions for the hKdV equation[J]. Nonlinear Analysis: Theory, Methods& Applications, 2009, 70(6): 2376-2381.

[8] Shivamoggi B K, Rollins D K. Generalized Painlevé formulation and Lie group symmetries of the Zakharov-Kuznetsov equation[J]. Physics Letters A, 1991,161(3): 263-266.

[9] 冯庆江,李岩,杨利垚. 用试探函数法求 Zakharov-Kuznetsov方程的孤子解[J]. 长春大学学报,2010,20(6):8-9.

[10] Yan Z L, Liu X Q. Symmetry reductions and explicit solutions for a generalized Zakharov–Kuznetsov equation[J]. Communications in Theoretical Physics,2006, 45(1): 29-32.

[11] 洪宝剑. KdV方程和Zakharov-Kuznetsov方程新的椭圆函数解[J]. 南京工程学院学报:自然科学版,2010,8(1):1-7.

[12] 王岗伟,张颖元.变系数 KdV-Burgers方程的精确解[J].聊城大学学报:自然科学版,2011,24(2):9-12.