基于图正则化非负矩阵分解的二分网络社区发现算法

汪 涛 刘 阳 席耀一

1 引言

随着Internet和移动通信技术的发展，大量异质网络数据在现实世界中广泛出现。这些网络往往由多种不同类型的异质节点构成，异质节点间的交互往往代表不同的连接关系。二分网络是异质网络的一种重要而具有代表性的表现形式，例如话题与文档，电影与电影评价、上网用户与网页，合著者与其合著论文等等。二分网络由两类节点群体组成，并具有特殊的二分结构：异质节点间存在连接，而同类节点间没有连接。当二分网络中的用户节点与目标节点建立边连接后，拥有共同连接节点的不同类型节点之间也具有了连通性。

社区作为网络中广泛存在的典型中尺度拓扑结构，能够直接有效地反映网络结构和特性，是理解复杂网络性质和局部功能的基础。单模的同质网络将社区定义为：网络中具有某种相似特性的节点集合，社区内部节点联系紧密而社区间联系相对稀疏。推广到二分网络，可以认为[1,2]：社区内部不同类型节点间的连接紧密，而社区间的不同节点间的连接则比较稀疏。二分网络中两类节点通过彼此间的作用、耦合形成各自所属的二分结构群组，说明同一社区内的目标节点群体与用户节点群体相互吸引，内聚性较强。因此，二分网络社区除了刻画传统意义上的网络结构特征，还有助于挖掘和理解网络中异质节点间的作用和关系。

近年来，基于原始的二分网络信息进行社区发现的研究思路开始引起关注。文献[3]将标签传播算法应用于二分网络社区发现，但其二分结构会引起节点标签振荡、稳定性差等问题。在文献[4～7]中分别提出了各自基于二分网络的模块度函数进行社区结构发现，这些方法沿用了单模网络环境下基于NG（Newman-Girvan）模块度来进行社区发现的思想。然而，二分网络的社区结构与常见的单模网络有着明显区别，即同类型节点没有连接，节点社区归属隐藏在二分结构下的异质节点连接关系里。二分网络这种特有的二分结构限制了基于共享邻接节点的传统节点相似性评估方法的有效性，使得仅仅依靠模块度指标对节点进行贪婪搜索易导致社区聚类陷入局部最优，难以有效地揭示二分网络的社区结构。然而，二分网络特有的二分结构限制了基于图分割、相似度聚类等传统算法的社区发现性能。因为二分网络邻接矩阵的行和列分别代表用户节点和目标节点，每个矩阵元素表示对应异质节点之间的连接关系。由于二分网络特征矩阵的行和列有很强的相关性，若单从某一维度进行社区发现，都将缺失另一维度的信息。而已有的 NMF解决方案大多基于最小化目标函数的拟合误差值，对二分网络中的两种节点子集进行简单化地独立处理，难以有效地揭示二分网络特殊的社区结构。

受非负矩阵分解启发，文献[8,9]分别提出了不同的非负矩阵分解模型来解决异质网络社区发现的问题，以挖掘异质网络中隐藏的结构与关系。尽管上述方法能够无监督地应用于复杂网络的社区发现，但是由于缺乏监督信息（约束条件或标签信息）使得矩阵分解的收敛速度和结果往往并不能令人满意，其不足主要体现在如下两个方面：（1）仅仅依靠原始数据信息（即类间信息）进行矩阵分解，忽略了类内节点内部重要的关联信息；（2）由于矩阵分解的迭代过程中，涉及到大量而密集的矩阵乘法和求逆运算，使得 NMF算法普遍存在时间复杂度高，收敛慢等问题。

为了解决上述问题，本文将基于图正则化的三重非负矩阵分解方法（Fast Nonnegative Matrix Tri-Factorization, F-NMTF）应用于二分网络社区发现，该模型在考虑异质网络的原始连接关系的同时，通过图正则化将用户子空间和目标子空间的内部连接关系作为图正则化约束，从而为NMTF模型引入了类间与类内信息以提高矩阵分解的精确度和稳定性，以改善二分网络社区发现的性能。

2 问题描述

非负矩阵分解是一种有效的矩阵低秩逼近方法，能够有效地揭示异质网络中多维数据潜在的结构特征，已经有多种方法被应用于文本挖掘和协同过滤等领域。然而，直接将 NMF应用于二分网络数据联合聚类，需要向其分解因子矩阵F,G同时施加非负正交的约束，约束太强会使矩阵分解的逼近程度大大降低，从而限制了社区发现的聚类性能。因此，这里引入一个新矩阵S以构建三重非负矩阵分解，该方法的优势主要体现在以下 3个方面[10]：（1）三重非负矩阵分解通过引入光滑因子矩阵S，极大改善了联合聚类过程中矩阵分解的自由度；（2）通过全面引入类间信息和类内信息，NMTF可结合双重子空间的流形约束提高联合聚类的性能；（3）优化后的迭代规则大大减小了NMTF的计算复杂度，能够快速地发现不同规模网络的各种潜在结构及社区间的交互规律。

图1所示的用户-网页网络即为一种典型的二分网络，其中用户和网页表示两类不同类型的异质节点，并可以进一步描述为由用户节点集U（Users）和目标节点集O（Objects）构成的二分网络模型。令G（ U, O, E）表示一个二分网络，U为用户节点集，O为目标节点集，E为边集。假设用户节点数|U |= m ，目标节点数|O | =n，给定二分网络G的邻接矩阵X ∈ ℝm×n，则NMTF定义为其中， ⋅为 Frobenius范数（简称 F范数），用来度量目标函数的逼近程度；NMTF通过寻找最大近似原始网络数据X的3个低阶因子矩阵来实现社区发现，F∈ℝm×r和G ∈ ℝn×r分别为用户子空间和目标子空间的划分矩阵，S ∈ℝl×r作为引入的光滑因子矩阵，表示二分网络中用户子空间与目标子空间的特征向量组之间的关联性。l和r表示用户子空间和目标子空间的聚类个数，由于基于非负矩阵分解的社区发现算法需要预设置网络中的社区个数，一般设置l = r 。由此，NMTF通过F,G共同揭示了二分网络隐藏的社区结构，将其划分为由二模（2-mode）节点混合组成的r个社区。

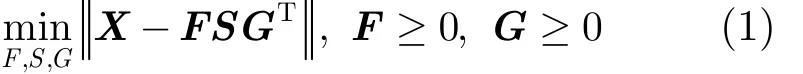
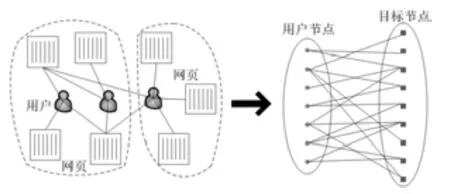
图1 基于用户-网页网络的二分网络模型

需要指出的是，在社区发现的研究背景下，非负矩阵分解后的维数r与二分网络中的社区个数相关，其取值直接影响着算法的收敛性能。理论上r≪（m, n），但r的取值过大或过小都会影响算法的收敛性速度和最终分解结果的精确度。目前，许多基于 NMF的社区发现方法[11,12]提出了不同的解决方案以预估网络中社区个数。由于文献[11]中的预估方法相对简单有效，能够准确地估计网络社区数量，故采用该方法确定r值。

3 基于图正则化的二分网络社区发现

本文基于图正则化的三重非负矩阵分解方法以二分网络矩阵非负分解的拟合误差作为目标函数，同时分别构建两种异质节点子空间的k-近邻图，并以其关联矩阵作为NMTF的正则化约束，并提出了一种F-NMTF的快速优化算法，从而在二分网络上实现基于图正则化的半监督社区发现。

3.1 二模节点的图正则化

基于图的半监督学习在实际中应用较为广泛，它主要通过构造图结构来引入半监督信息，以辅助数据聚类。本文的F-NMTF通过分别构建二模节点的近邻图来估算用户子空间和目标子空间的结构特征，并作为正则化约束项添加到 NMTF目标函数中，以增强非负矩阵分解的正交性和收敛性。这里首先分别构建子空间U和O的k-近邻图，并以该关联矩阵作为类内（Intra-type）信息作为 NMTF模型的正则化约束。该k-近邻图有效融合了同类节点的相似性信息（即类内信息）。

定义 1 定义用户子集 NU关于k-近邻图的权重矩阵WF为

其中， N （Ui）为用户节点Ui的k-最近邻集合，并采用0-1加权方式创建k-近邻图的权重矩阵：如果Ui是 Uj的k近邻节点，或 Uj是 Ui的k近邻节点时，WF（ i, j）=1；否则，WF（ i, j）=0。这里可以引入权重矩阵进一步凸显同类节点间连接模式的差异性，并以此作为正则化项来优化目标函数。

根据流形假设[13]，异质网络数据经非负矩阵分解后，同类节点间的局部邻域结构在低维特征空间中能够得以保持，则当高维空间中距离较近的向量Xi.,Xj.映射到对应的低维流形上 Fi.,Fj.时，距离依然较小。从而定义基于用户子空间的正则化项为

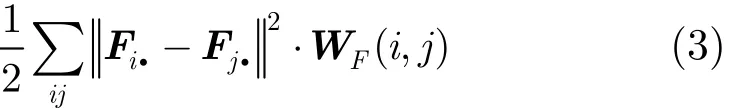
其中⋅表示Frobenius范数。若令矩阵F的行向量Fi.,Fj.分别对应用户节点 Ui,Uj的社区指示向量，该正则化项刻画了用户子集社区划分的平滑程度。

由矩阵的两个性质：tr（A B ）= tr（B A ）和tr（A）= t r（AT） ，式（3）可以进一步转换为

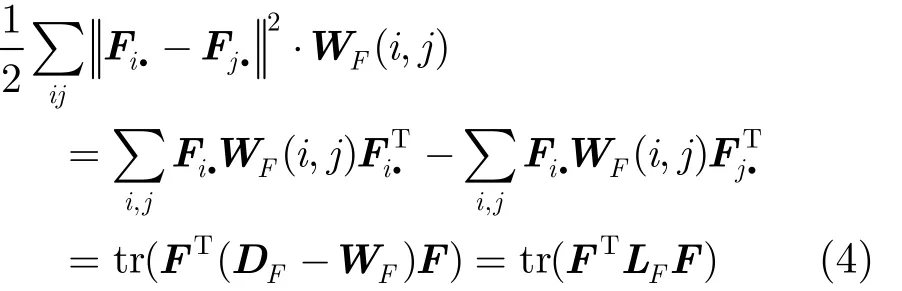
其中， LF= DF-WF表示用户子集 NU的拉普拉斯矩阵，其标准化拉普拉斯矩阵为 LF=I-WF。 DF表示用户节点度的对角矩阵，即

定义 2 定义目标子集 NO关于k-近邻图的权重矩阵WG为

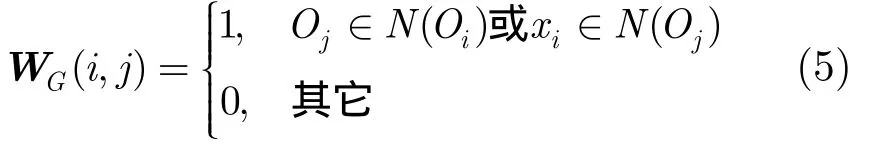
其中， N （ Oi） 为目标节点 Oi的k-最近邻集合。

同理，当高维空间中距离较近的向量 Xi.,Xj.映射到对应的低维流形上 G.i,G.j时，距离依然较小，从而定义基于目标子空间的正则化项为

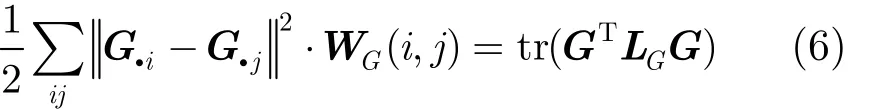
类似地， LG= DG-WG表示目标子集 NO的拉普拉斯矩阵，其标准化拉普拉斯矩阵为 LG=I -WG。 DG是用户节点度的对角矩阵，即 DG（j, j） =∑ixij。若令矩阵G的行向量 G.i,G.j分别对应用户节点 Oi,Oj的社区指示向量，该正则化项刻画了目标子集社区划分的平滑程度。需要指出的是，通过增加图正则化项，能够将数据内在的结构特征作为约束信息引入到非负矩阵分解模型中，以优化二分网络社区发现。

3.2 一种基于图正则化的三重非负矩阵分解算法

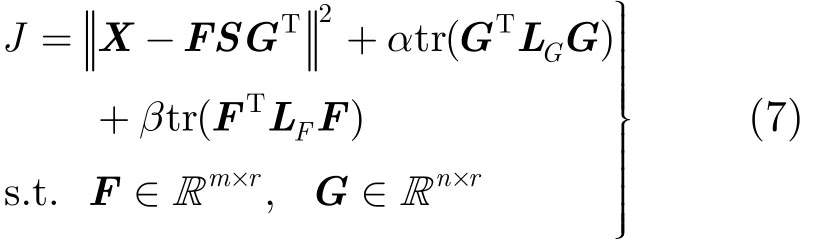
在三重非负矩阵分解模型中，引入二模节点的双重正则化约束，从而将式（1）转化为约束优化求解问题，目标函数定义为其中，α≥0,β≥0表示正则化约束系数，用于平衡第2正则项和第3正则项在目标函数中的权重。当α= 0 时，该模型（式（7））转化为单一的图正则非负矩阵分解模型[14]；而当 α =β=0时，则该模型（式（7））转化为一般的非负矩阵分解模型（式（1））。

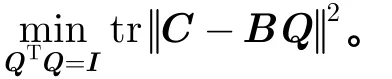
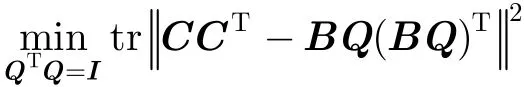
将定理 1 应用到目标函数（式（5）-式（7））中，其中的正则约束项可分别改写为

由此，F-NMTF的目标函数可转化为最小化问题：

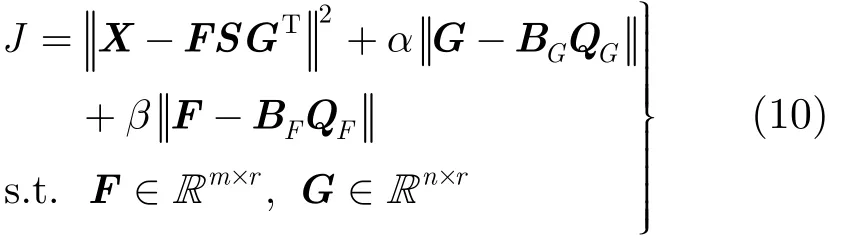
其中， BF和 BG分别源自标准化拉普拉斯矩阵 LF,LG。式（10）给出了基于图正则化的 NMTF联合聚类模型。该模型基于用户子空间和目标子空间的流形结构，构建二者的k-近邻图的权重矩阵添加到目标函数中作为正则化项。由此，F-NMTF成功引入了异质节点的类内信息以辅助并改善二分网络的社区发现。

3.3 算法优化

由于NMTF模型是关于3个因子矩阵F,S和G的非凸函数，难以直接获取其全局最优解。因此，本节提出了一种乘性交替迭代算法，即每次迭代都固定两个因子矩阵为最新值，求解剩下的因子矩阵。于是，NMTF模型转化为关于单一变量的凸优化问题。通过交替地迭代更新，从而得到问题的稳定点或局部极值点。不同于 NMF分解中引入拉格朗日乘子进行矩阵乘性迭代的一般思路，F-NMTF算法对最小化子问题进行奇异值分解以期进一步简化。优化后的迭代算法主要运用矩阵向量进行乘法运算，使得在每步迭代中求解因子矩阵较为简便，从而加速算法收敛。

定理2 定义一个优化问题为

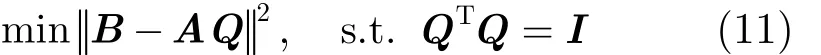
令H = ATB，且其奇异值分解（Singular Value Decomposition, SVD）为 H =UΛ VT。当矩阵A和B确定时，矩阵Q的最优解为 Q = UVT。

证明 根据矩阵的迹性质：tr（A B ） = tr（B A ） 和tr（A） = tr（AT），当矩阵B确定时，min B - AQ2等同于tr（QTH ）。通过奇异值分解，得到 t r（QTH）=tr（Q U Λ VT）=tr（ΛVTQU ） = t r（Λ Z ）=，其中λii和zii分别表示Λ和Z对应的矩阵元素。

令Z =VTQU为正交矩阵，即 ZTZ =I,zii≤ 1 , λii≥ 0 是矩阵H的奇异值。由此，进一步得到 t r（QTH ） = ∑iλiizii≤ ∑iλii。 当 Z =I时，tr（QTH）获得其最大值，由此说明Q = UZTVT=UVT是优化问题min B - AQ2的最优解，则定理2得证。

根据定理 2, F-NMTF优化问题可以有效地分解为两个关于较小规模矩阵的子问题，涉及到的矩阵乘法运算也会相应减少。因此，该方法更应用于大规模的真实异质网络数据。这里首先确定因子矩阵F和G，对式（10）求偏导以求解S：

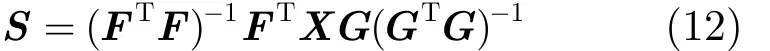
确定S后，将目标函数（式10）的第2和第3正则项分解为两个子问题

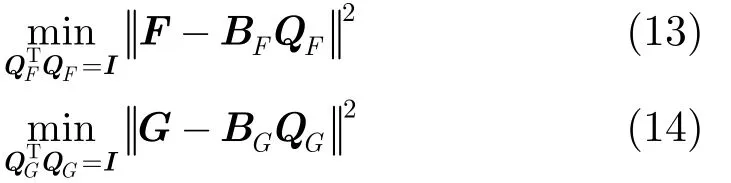
FF

下面对两个子问题交替迭代求其最小解，这里分别求出每一个参数的偏导数，然后对偏导数求解以更新参数。对于子问题1，这里确定矩阵F,S和QG以迭代更新剩余变量G。令 YG=FS, ZG=BGQG，则原目标函数被简化为其中，（ZG）i.表示矩阵 ZG的第i个行向量。

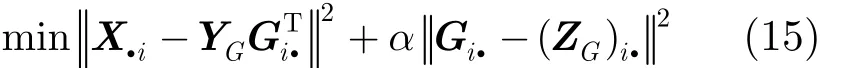
由于分解因子G为目标节点子空间的社区指示矩阵，假定 Gi.表示目标节点 Oi的社区指示向量，则对简化后的目标函数求偏导，选择与其具有最小近似误差的社区j作为该节点的归属社区，从而将 Gij设置为1，同一行的其他元素设置为0，得到分解后的矩阵G为

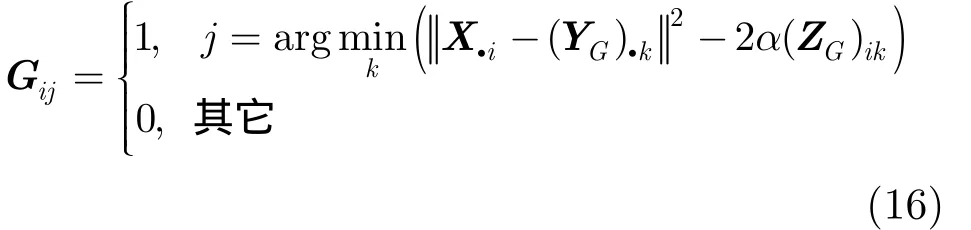
其中，argmink（X.i- （YG）.k2-2α（ZG）ik）返回社区集合中与目标节点 Oi有最小近似误差的社区标号。

对于子问题 2，确定矩阵G,S和 QF以迭代更新剩余变量F。令YF=SGT,ZF=BFQF，则原目标函数被简化为其中，（ZF）.j表示矩阵 ZF的第j个列向量。

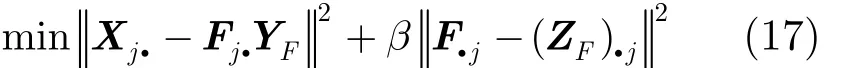
类似地，由于分解因子F为用户节点子空间的社区指示矩阵，假定 Fj.表示用户节点 Uj的社区指示向量，则对简化后的目标函数求偏导，选择与其具有最小近似误差的社区i作为该节点的归属社区，从而将 Fji设置为 1，同一行的其他元素设置为 0，得到分解后的矩阵F为

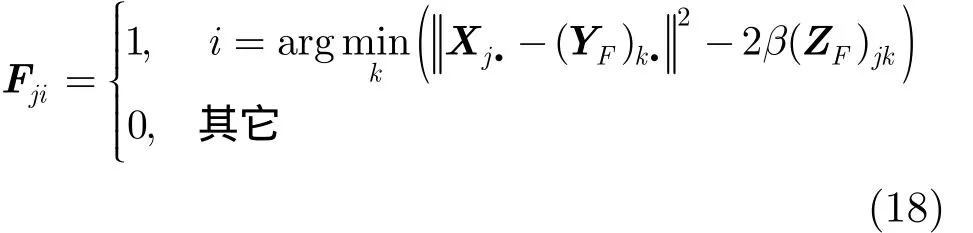
其中，argmink（Xj.- （YF）k.2-2β（ZF）jk） 返回社区集合中与用户节点 Uj有最小近似误差的社区标号。

重复迭代上述的矩阵分解过程，并不断更新因子矩阵F,S和G，直至目标函数值趋于收敛或达到最大迭代次数。迭代结束后，最终得到的矩阵F和G分别对应对用户子空间和目标子空间的社区划分，二者共同决定二分网络社区结构。其中，列向量 F.i与行向量 Gi.对应第i个网络社区。对于 Fij=1，则说明用户节点 Ui隶属于社区j；对于 Gij=1，则说明用户节点 Oj隶属于社区i。对因子矩阵F,G的元素进行 0,1赋值，由此可以直接推导二分网络中异质节点的社区归属。

基于三重非负矩阵分解的 F-NMTF算法开销主要包括计算目标函数J和因子矩阵分解迭代。算法每次迭代需要同步更新 3个不同规模的因子矩阵：基矩阵F∈ℝm×r，光滑因子矩阵S ∈ ℝr×r和系数矩阵G ∈ ℝn×r。由于 r ≪ （m, n），其迭代求解的计算复杂度为 O （ tr m n），则F-NMTF的算法复杂度为O（ tr m n）, t为算法迭代次数。优化后的迭代算法对因子矩阵F,G的元素进行0,1赋值，并主要基于向量进行矩阵分解运算，从而简化了每步迭代求解，使其能够适用于较大规模的网络数据。

4 实验与分析

实验同时基于计算机生成网络和真实网络进行测试，并采用不同的指标来评估二分网络社区发现算法的性能。由于计算机生成网络的社区结构已知，采用经典标准互信息（Normalized Mutual Information, NMI）和运行时间作为衡量标准。对于未知结构的真实网络，则采用二分模块度（bipartite modularity）和运行时间。需要指出的是，二分模块度是文献[4]中扩展自模块度的指标，专门应用于衡量二分网络的社区划分质量，并被大量相关工作中所采纳接受。为全面分析比较二分网络社区发现算法的性能，实验选取Guimera[7], NMF[15], GNMF[14]和BNMTF[16]4种典型算法作与F-NMTF算法进行对比。其中，Guimera是关于二分网络社区发现的基准算法，NMF, GNMF与BNMTF则是近年来提出的基于NMF的社区发现方法。

对于 NMF方法（NMF, GNMF, BNMTF和F-NMTF），根据文献[17]设置最大近邻数k为{1,2,,…10}，正则化系数α和β为0.1。此外，根据文献[11]提供的方法计算网络社区数目，该方法已被证明能够较为准确地预测网络社区的数量。每个方法在所有网络数据上重复实验50次，并计算度量指标的均值。

4.1 计算机生成网络

计算机生成网络采用文献[7]提出的二分网络基准生成模型。该模型可以灵活设置各项网络参数，以生成较高质量的二分网络标准数据集。一般来说，社区内连接概率值inρ越高，则说明二分网络的社区结构越强；反之，随着outin/ρρ的递增，二分网络的社区结构逐步趋于模糊，社区发现也就越困难。通过设置参数inρ和outρ控制二分网络社区结构的强弱程度，从而有效地验证不同算法的社区发现的性能。实验中生成9组网络测试数据集，每组包含10个同样配置的二分网络，outin/ρρ间隔为0.1，具体配置如表1所示。

由于计算机生成网络社区结构已知，实验从 9组测试数据集中每组随机抽取5个网络，分别计算各种算法在不同测试数据集下的指标均值。如图2（a）所示，当ρout/ρin逐步递增，所有算法的运行时间急剧上升，不同算法间的运行时间差也逐步扩大。这是因为二分网络的社区结构较弱时，导致社区发现困难程度较大，需要反复迭代使得矩阵分解消耗大量的运行时间。由于Guimera算法不同于NMF类算法，基于最大化模块度进行贪婪聚类，因而试验中针对性地比较NMF类4种算法的运行时间。而在NMF类算法中，F-NMTF运行时间短，收敛速度较快；且随着二分网络社区结构的弱化，其快速收敛的优势也逐步扩大。说明F-NMTF计算复杂度低，相比其它 NMF算法具有更好的收敛性和适应性。

表1 网络配置参数

图2（b）给出了5种算法在计算机生成网络下社区发现的NMI均值。当 ρout/ρin≤ 0 .4时，二分网络的社区结构较为明显，5种算法都表现出良好的社区发现性能，NMI均值都大于 0.8。其中 Kmeans社区发现的准确率略差。但当 ρout/ ρin≥ 0 .5时，二分网络的社区结构趋于模糊，使得社区发现准确性下降，5种算法的NMI值均呈现下降趋势，社区发现的精确度急剧下降。其中，F-NMTF仍保持了相对较高的NMI值，F-NMTF的NMI均值比NMF提升了5.83%，相比GNMF算法则提升了3.13%。这说明 F-NMTF算法对二分网络社区发现的准确率较优且维持在较高水平，能够发现更接近于标准二分网络的真实社区结构。

4.2 真实网络

真实网络相比计算机生成网络更不规则，因而其社区结构往往也更加复杂。这里采用5个具有不同规模的真实二分网络数据集：南方妇女网络（Southwomen）[18]、苏格兰公司网络（Scotland）[19]、论坛话题网络（Irvine forum）[20]、电影评分网络（Movielens）[21]、2004年凝固态物理引文网络（Condmat）[22]来进一步测试算法性能，表2描述了这些真实网络的基本属性。这里根据文献[11]提供的方法预估真实网络数据中的社区数目r，同时也就确定了NMF算法中因子矩阵的维数。

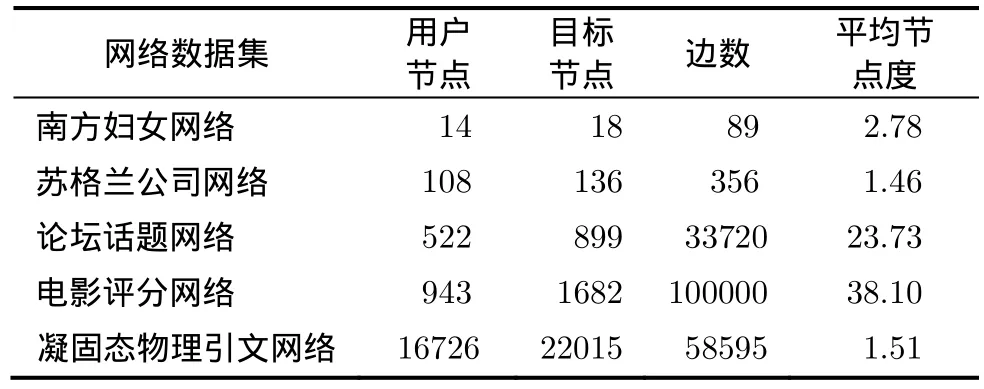
表2 实验中真实网络的基本属性

由于真实二分网络的社区结构未知，这里采用运行时间和二分模块度来衡量不同算法社区划分质量的优劣，以此作为对计算机生成网络实验的补充和佐证。如表3所示，NMF方法的时间复杂度明显要高于Guimera算法。在NMF算法中，F-NMTF算法的运行时间最接近于Guimera算法，这说明该算法有效地加快了非负矩阵分解的收敛速度，相比同类算法消耗了最少的运行时间。但由于网络规模不同，F-NMTF在不同二分网络下社区发现的时间增益也呈现出较大差别。对于较大规模的二分网络，F-NMTF时间复杂度较低的优势更为明显。

表4给出了5种算法社区发现的二分模块度BQ值，准确的网络社区划分对应于较大的BQ 值。由于网络结构不同，使得二分网络社区发现的BQ 值也处于不同的水平。Guimera是基于二分模块度最大化的社区发现算法，与NMF算法相比，其BQ 值较优；但作为模块度优化的方法存在分辨极限（resolution limit）等问题。比较5种NMF算法发现：F-NMTF在 5种真实二分网络上获得了较大的二分模块度QB，说明该算法的社区发现质量最优。对于南方妇女网络，苏格兰公司网络，论坛话题网络3个具有较弱社区结构的二分网络，F-NMTF算法对于社区发现准确率的改善幅度较小。对于电影评分网络，凝固态物理引文网络具有较强社区结构的二分网络，F-NMTF算法的社区发现准确率改善幅度较大。对比NMF, BNMTF算法，F-NMTF的BQ 值在前3个真实网络上平均增幅分别为0.057和0.011；在后两个真实网络上，F-NMTF的BQ 值平均增幅分别为0.036和0.015。

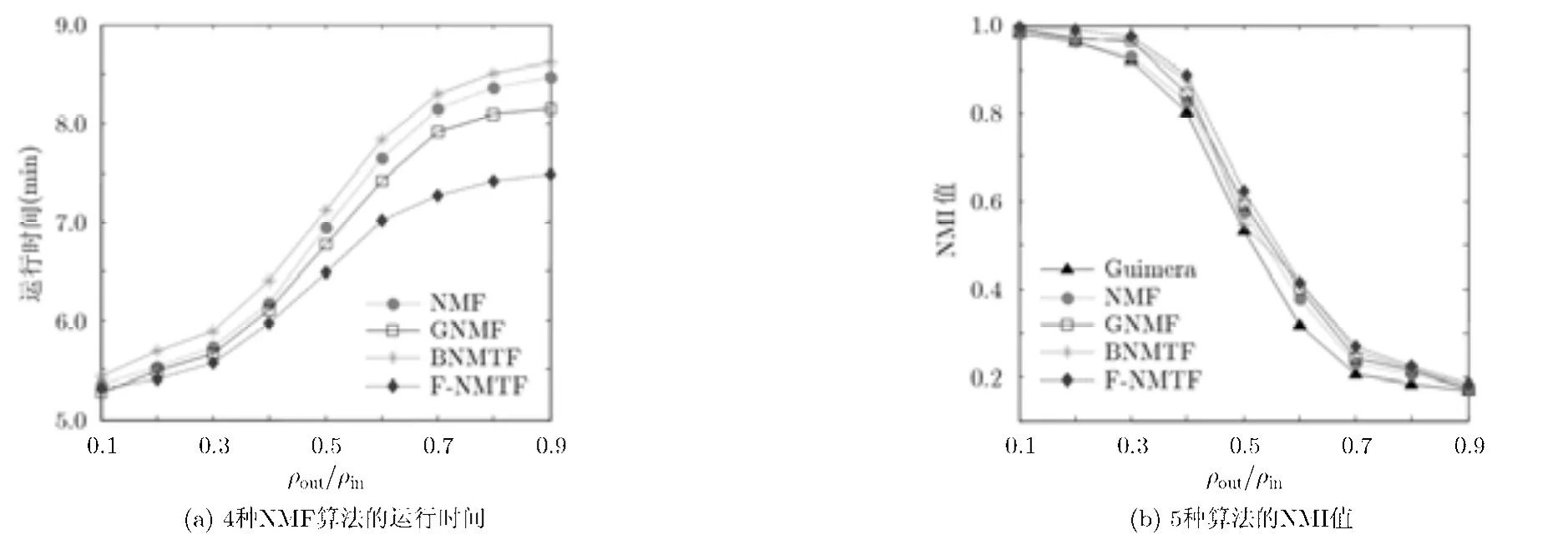
图2 社区发现算法在计算机生成网络上的性能对比

表3 真实网络中5种算法社区发现的运行时间

表4 真实网络中5种算法社区发现的二分模块度

综合 F-NMTF算法在计算机生成网络和真实网络中的表现，可以得出结论：相比 Guimera，GNMF等算法，通过图正则化引入类内信息的F-NMT算法更适合具有特殊二分结构的二分网络，从而挖掘得到更真实有效的社区结构。

5 结束语

本文提出了一种基于图正则化的三重非负矩阵分解算法应用于二分网络社区发现，该方法通过分别构建两类异质节点的 k-近邻图来估计用户子空间和目标子空间的结构特征，将其作为正则化约束项添加到F-NMTF目标函数中，从而同时引入了类间信息与类内信息，以增强非负矩阵分解的正交性和收敛性；同时将NMTF模型分解为两个关于交替求解最小化函数的子问题，简化矩阵分解迭代以加快收敛，从而改善 NMF方法时间复杂度高等问题。实验和分析证明：对于计算机生成网络和真实网络，F-NMTF的社区划分方案均表现出有较高的准确率和稳定性，能够准确有效地挖掘二分网络的社区结构。同时，如何将非负矩阵分解进一步应用于扩展到多模或多关系异质网络的社区发现，并保证复杂网络环境下社区划分的合理性和有效性，将是下一步工作的研究重点。

[1] 全佳妮. 基于二分网络的协同推荐研究[D]. [硕士论文], 苏州大学, 2012.Quan Jia-ni. Research on collaborative recommendation based on bipartite network[D]. [Master dissertation], Suzhou University, 2012.

[2] 熊湘云. 基于二分网络的多维度推荐技术研究[D]. [硕士论文],苏州大学, 2013.Xiong Xiang-yun. Research on multi-dimensional recommendation based on bipartite network[D]. [Master dissertation], Suzhou University, 2013.

[3] Liu X and Murata T. How does label propagation algorithm work in bipartite networks[C]. Proceedings of the IEEE International Joint Conference on Web Intelligence and Intelligent Agent Technology, Milano, Italy, 2009: 5-8.

[4] Barber M J. Modularity and community detection in bipartite networks[J]. Physical Review E, 2007, 76（6）: 066102.

[5] Murata T. Detecting communities from bipartite networks based on bipartite modularities[C]. Proceedings of the Computational Science and Engineering, Vancouver, Canada,2009, 4: 50-57.

[6] Suzuki K and Wakita K. Extracting multi-facet community structure from bipartite networks[C]. Proceedings of the Computational Science and Engineering, Vancouver, Canada,2009, 4: 312-319.

[7] Roger Guimera, Marta Sales Pardo, Luis A, et al.. Module identification in bipartite and directed networks[J]. Physical Review E, 2007, 76（3）: 036102.

[8] Tang L, Wang X, and Liu H. Community detection via heterogeneous interaction analysis[J]. Data Mining and Knowledge Discovery, 2012, 25（1）: 1-33.

[9] Sun Y, Tang J, Han J, et al.. Community evolution detection in dynamic heterogeneous information networks[C].Proceedings of the 8th Workshop on Mining and Learning with Graphs, Washington DC, USA, 2010: 137-146.

[10] Wang H, Nie F, Huang H, et al.. Nonnegative matrix trifactorization based high-order co-clustering and its fast implementation[C]. Proceedings of 11th International Conference on Data Mining, Vancouver, Canada, 2011:774-783.

[11] Nguyen N P, Dinh T N, Tokala S, et al.. Overlapping communities in dynamic networks: their detection and mobile applications[C]. Proceedings of the 17th Annual International Conference on Mobile Computing and Networking, Las Vegas,USA, 2011: 85-96.

[12] Zhang Z Y, Wang Y, and Ahn Y Y. Overlapping community detection in complex networks using symmetric binary matrix factorization[J]. Physical Review E, 2013, 87（6）:062803.

[13] Li Ping, Bu Jia-jun, Chen Chun, et al.. Relational multimanifold coclustering[J]. IEEE Transactions on Cybernetics, 2013, 43（6）: 1871-1881.

[14] Cai D, He X, Han J, et al.. Graph regularization non-negative matrix factorization for data representation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2011, 33（8）: 1548-1560.

[15] Wang F, Li T, Wang X, et al.. Community discovery using nonnegative matrix factorization[J]. Data Mining and Knowledge Discovery, 2011, 22（3）: 493-521.

[16] Zhang Yu and Yeung Dit-Yan. Overlapping community detection via bounded nonnegative matrix tri-factorization[C]. Proceedings of the 18th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,Beijing, China, 2012: 606-614.

[17] Shang Fan-hua, Jiao L C, and Wang Fei. Graph dual regularization non-negative matrix factorization for coclustering[J]. Pattern Recognition, 2012, 45（6）: 2237-2250.

[18] Southwomen network. http://konect.uni-koblenz.de/networks/Southwomen[OL]. 1930.

[19] Scott J and Hughes M. The Anatomy of Scottish Capital:Scottish Companies and Scottish Capital[M]. London: Croom Helm, 1980: 291.

[20] Opsahl T. Triadic closure in two-mode networks: redefining the global and local clustering coefficients[J]. Social Networks,2013, 35（2）: 159-167.

[21] MovieLens network. http://konect.uni-koblenz.de/networks/movielens-100k_rating[OL]. 2009.

[22] Arxiv cond-mat network. http://konect.uni-koblenz.De/networks/opsahl-collaboration[OL]. 2004.