腔场-激子-可运动腔镜的纠缠
腔场-激子-可运动腔镜的纠缠
付长宝,王希英
(通化师范学院 物理学院,吉林 通化 134002)
摘要:本文针对由典型光力系统和量子阱耦合的杂化光力系统,提出了一个在该系统中实现量子关联的方案.结果表明,系统处于稳态时,由于在腔场、量子阱内的激子和运动腔镜之间的纠缠共享,系统将出现三体和两体连续变量纠缠.与以往的文献相比,本文的意义在于由于驱动系统的光为中红外波段的单色光,在本文中光热力效应可以被安全地忽略.
关键词:量子光学;光力学;纠缠
DOI:10.13877/j.cnki.cn22-1284.2015.10.015
收稿日期:2015-09-28
基金项目:吉林省教育厅科学技术研究项目“基于腔光力学系统的光存储研究”(2013. 387)
作者简介:付长宝,男,吉林九台人,讲师,博士研究生.
中图分类号:O432文献标志码:A
量子纠缠的制备自量子纠缠概念被提出就一直备受实验和理论研究者的关注.实验上,人们利用微观量子系统如光子[1]和原子[2]进行量子纠缠制备的技术已十分成熟.作为研究系统行为由量子到经典过度的第一步,几个实现小组利用宏观系统[3-4]进行量子纠缠制备的工作最近也已经被报道.由于腔光力系统把光学自由度和力学自由度有机地结合在了一起,因此,腔光力系统很自然地成为人们利用宏观系统进行纠缠制备时重点关注的系统.典型的光力系统[5]是一个一端可运动的法布里-珀罗光学腔系统.理论上,人们已经提出利用典型光力系统实现两体连续变量纠缠制备的方案,并且发现该系统中的两体连续变量纠缠可以通过光热力[6]和周期调制[7]进行操控.将典型的光力系统和其它的物理实体进行耦合,人们还可以构建更为复杂的光力系统-杂化光力系统,例如可以利用典型光力系统与LC电路[8],与单个被诱捕的原子[9]以及与冷原子晶格[10]等耦合构建一系列的杂化光力系统.由于构建的杂化光力系统具有许多潜在的量子性质,因此杂化光力系统目前已成为人们探究物理系统量子性质时主要关注的系统.理论上,到目前为止,人们已提出多个利用较高频率的单色光驱动杂化光力系统实现三体和两体连续变量纠缠的方案[11-13].众所周知,当驱动光频率较高时,腔场会导致可运动腔镜内原子的激发,此时光热力效应会十分地显著.但在这些基于高频单色光驱动的杂化光力系统实现的三体和两体连续变量纠缠方案中,为了简化问题,光热力效应都被人为地不安全地忽略了.
基于以上原因,本文针对由典型光力系统和量子阱耦合的杂化光力系统,提出了一个光热力效应可以被安全忽略的量子关联方案.结果表明,系统处于稳态时,由于在腔场、量子阱内的激子和运动腔镜之间的纠缠共享,系统将出现三体和两体连续变量纠缠.
1模型和方程
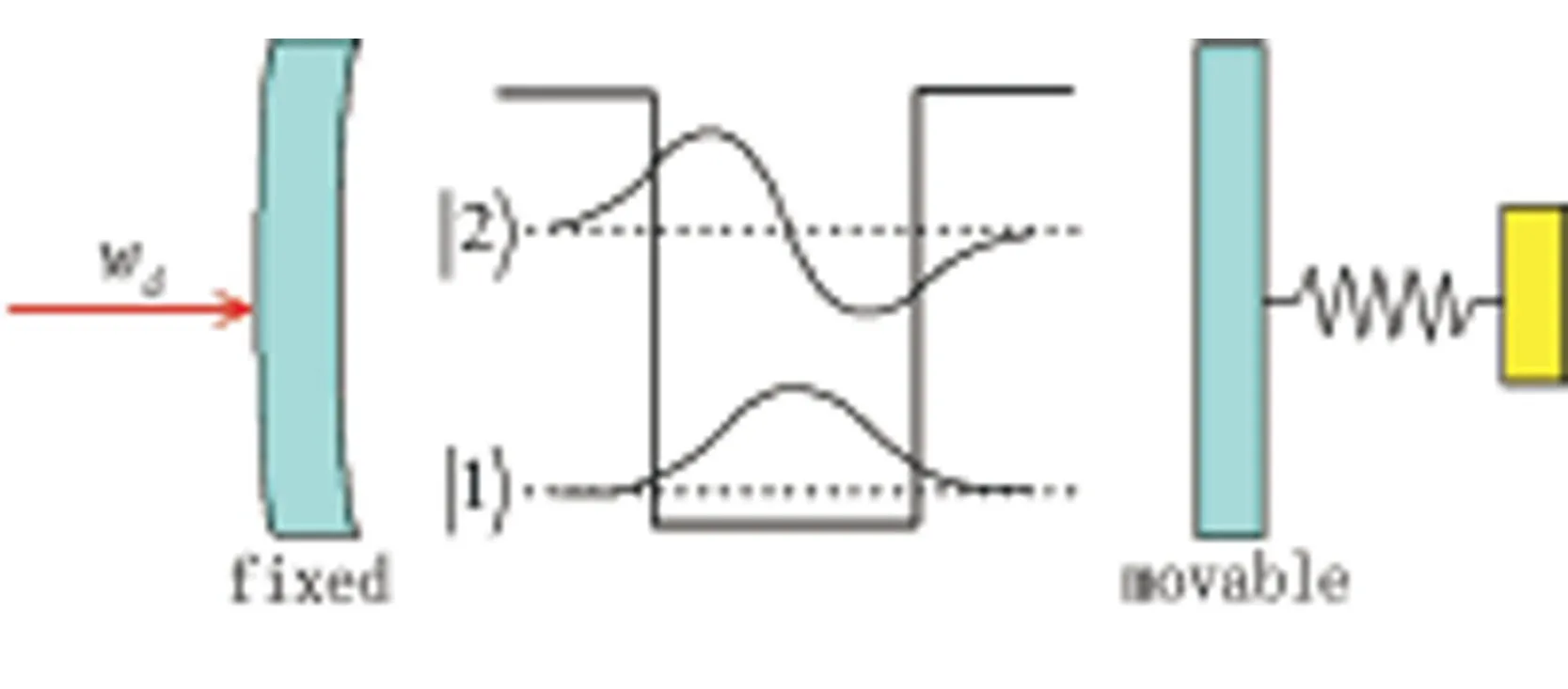
图1杂化光力系统示意图.系统由典型光力系统和量子阱耦合构成.典型光力系统左侧腔镜是固定的,右侧腔镜是可运动的.频率为ωd的驱动场经左侧腔镜入射到腔内,激发频率为ωc的腔场.|1〉和|2〉分别为量子阱内激子的基态和第一激发态.量子阱上的实线表示激子基态和第一激发态的波函数.
如图1所示,我们考虑由典型光力系统和量子阱耦合的杂化光力系统,典型的光力系统左侧腔镜是固定的,右侧的腔镜是可运动的.运动的腔镜可以被看作质量为m本征频率为ωm的量子谐振子.一个有限深的单量子阱被镶嵌在腔内,|1〉和|2〉分别为量子阱内激子的基态和第一激发态.频率为ωd输入功率为Pd的驱动场由左侧腔镜入射到腔内激发频率为ωc的腔场.在以驱动场频率ωd为参考的旋转参考系下,系统哈密顿为
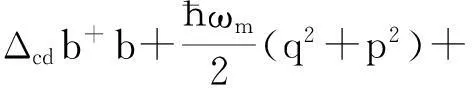
ħgce(a+b+b+a)-ħgcma+aq+iħEd(a+-a),
(1)
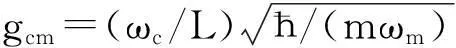
从系统的哈密顿出发,考虑系统的耗散和量子噪声,可以获得描述系统随时间演化的动力学方程
∂tq=ωmp,
∂tp=-ωmq+gcma+a-γmp+ξ,
∂ta=-(κc+iΔcd-igcmq)a-igceb+
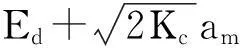

(2)
在方程(2)中,γm表示可运动镜子的衰减速率,κc表示激子的衰减速率.ξ表示可运动镜子的布朗噪声,满足关联函数[14]
(3)
其中,kB表示玻尔兹曼常数,T表示环境温度;am和bm分别表示作用于腔场和量子阱内激子的量子噪声,满足关联函数[15]
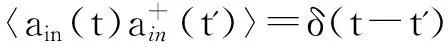
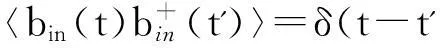
(4)
为了探究系统处于稳态时,在腔场-激子-可运动腔镜之间的三体和两体连续变量纠缠,我们需要分析系统稳态附近的量子涨落行为.在强驱动条件下,方程(2)中的每个算符都可以改写为稳态解加上其量子涨落的形式: a=αs+δa,b=βs+δb,p=ps+δp,q=qs+δq.将改写后的算符代入方程(2),从方程(2)可以分离出两组方程.一组为稳态解的方程
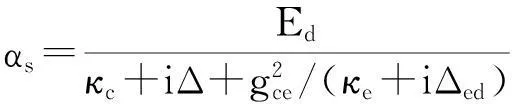

Ps=0,
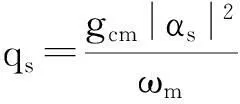
(5)
∂t(δq)=ωmδp,
∂t(δp)=-ωmδq-γmδp+GδXc+ξ,
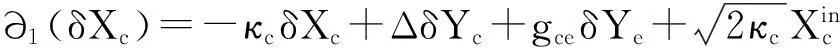
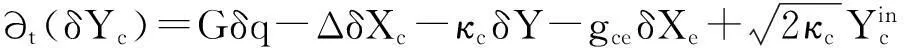
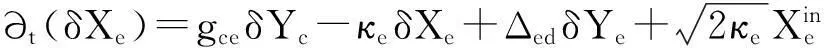
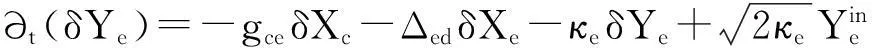
(6)
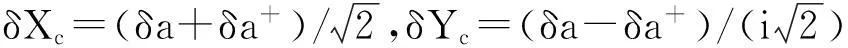
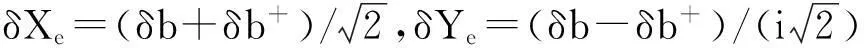
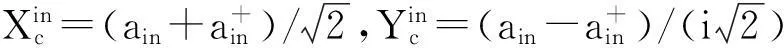
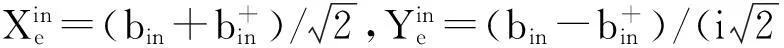
方程组(6)是关于系统涨落的线性方程组,可以简写为如下的矩阵形式
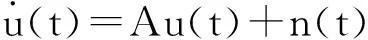
(7)
在方程(7)中,
u(t)=
(δq(t),δp(t),δXc(t),δYc(t),δXe(t),δYe(t))T,
n(t)=
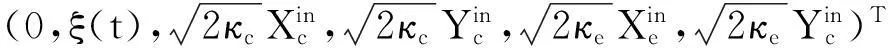
其中T表示转置,系数矩阵A为
(8)
我们知道,当系数矩阵A的所有本征值的实部都为负数时,系统的稳态是稳定的.利用劳斯霍尔维茨准则[16],我们可以很容易地获得系统稳态稳定的条件,但由于其过于复杂,在这里略去它的具体表达式.下面,将在系统稳态稳定的条件下,探讨在稳态附近系统的量子涨落.
由于系统量子涨落所满足的方程组是线性方程组,量子噪声是高斯噪声,因此,系统量子涨落的稳态一定为三体高斯态,可以利用矩阵元为
Vij=
AV+VAT=-D
(9)
为了度量系统处于稳态时,在腔场-激子-可运动腔镜之间的三体和两体连续变量纠缠,我们需要对三体系统中所有两体子系统连续变量纠缠进行度量.任一两体子系统可以通过对余下的第三子系统求迹获得.任一两体子系统连续变量纠缠可利用负对数[18]EN进行度量,EN定义为
EN=max[0,-ln2η-]
(10)
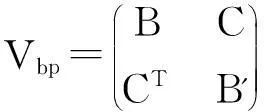
(11)
在方程(10)中,∑(Vbp)≡detB+detB'-2detC.
2结果与讨论
在这部分,我们数值模拟系统处于稳态时,在腔场-激子-可运动腔镜之间的三体和两体连续变量纠缠,因此需要对三体系统中所有两体子系统连续变量纠缠进行数值模拟.为了方便,我们利用Ecm,Eme,Ece分别表示腔场-可运动腔镜,可运动腔镜-激子,腔场-激子两体连续变量纠缠的负对数.同时考虑潜在的实验研究,我们选择一组实验上可行的参数:L=250μm,κc=78.5MHz,ωd=244.01THz(7725nm),Pd=35mW;m=10ng,ωm=62.8MHz,γm=628HZ;gce=37.7MHz,gcm=399Hz,κe=30MHz.
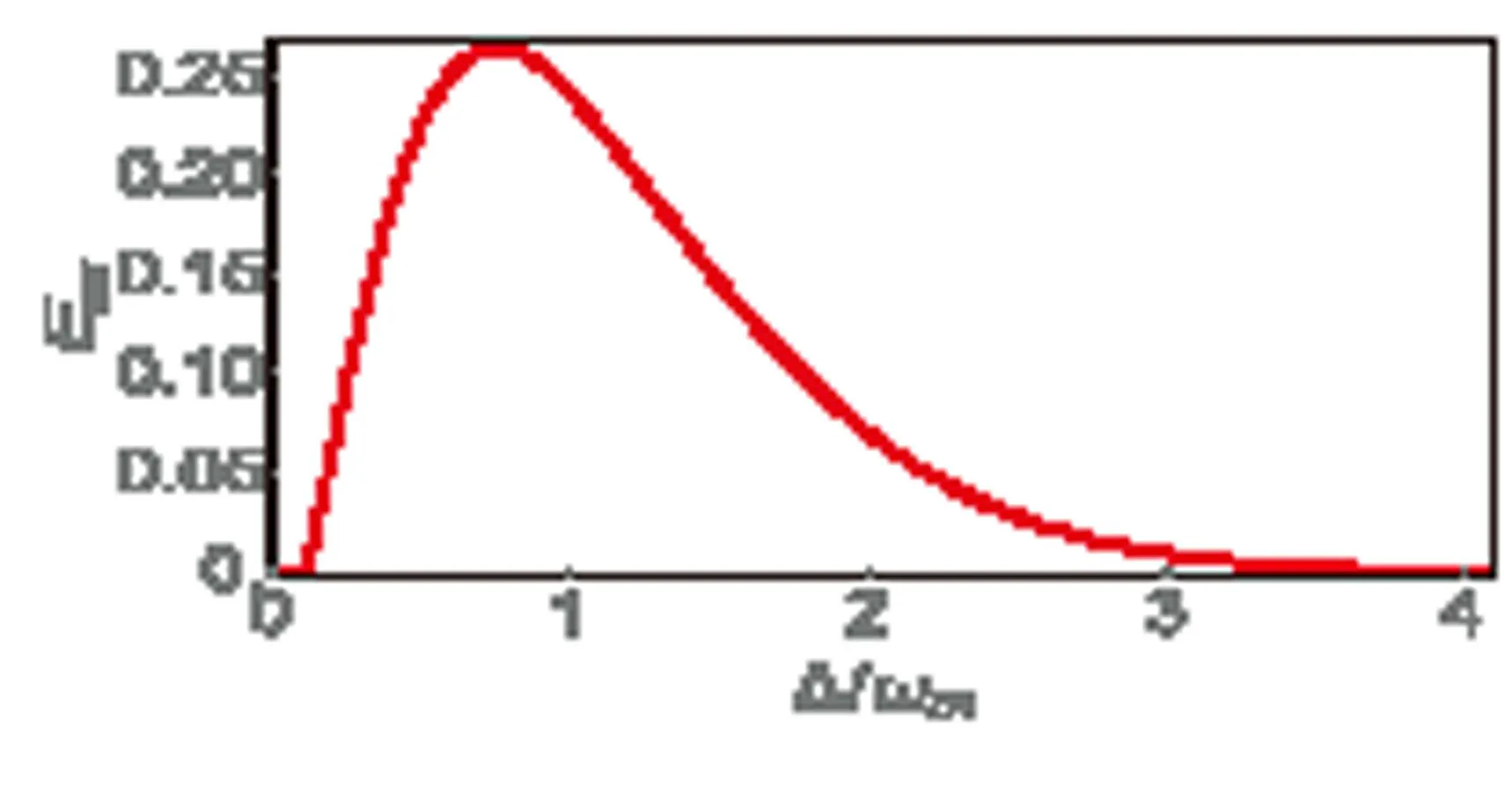
图2 腔场-可运动腔镜之间的连续变量纠缠E cm
在图2中,我们给出了当温度T=0.6K时,Ecm随Δ/ωm的变化曲线.我们发现,腔场-可运动腔镜之间的连续变量纠缠仅在Δ/ωm=1附近存在.这是因为进入腔内的驱动场被可运动腔镜散射,形成斯托克斯(ωd-ωm)和反斯托克斯(ωd+ωm)边带.当腔场与驱动场的反斯托克斯边带共振(Δ/ωm=1)时,可运动腔镜一方面被腔内泄露的反斯托克斯光子冷却,另一方面与余下的斯托克斯光子量子关联形成腔场-可运动腔镜间的连续变量纠缠.
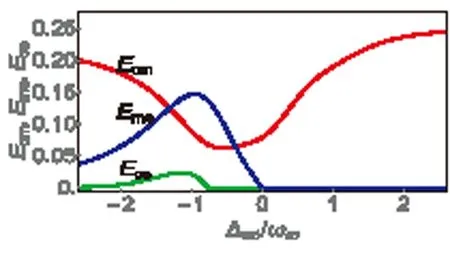
图3 腔场-可运动腔镜,可运动腔镜-激子,腔场-激子两体
在图3中,我们给出了当Δ/ωm=1时,Ecm,Eme,Ece随Δed/ωm的变化曲线.我们发现三个两体子系统的连续变量纠缠仅同时在Δed/ωm=-1附近出现.腔场-可运动镜子之间连续变量纠缠的减小伴随着可运动镜子-激子和腔场-激子之间连续变量纠缠的增加.这是因为当激子与驱动场的斯托克斯边带(Δed/ωm=-1)共振时,腔场-可运动镜子之间的连续变量纠缠(图2)被部分地分配给了可运动镜子-激子和腔场-激子系统.三体系统中所有两体子系统连续变量纠缠同时出现,意味着系统本身处于一个完全不可分的三体连续变量纠缠中.
与以往的文献相比,本文的意义在于我们所使用的驱动杂化光力系统的光其波长为λd=7725nm属中红外波段的单色光,由于驱动光频率较低,腔场几乎不会导致可运动腔镜内原子的激发,此时光热力效应可以被安全在忽略.
3结论
本文针对由典型光力系统和量子阱耦合的杂化光力系统,提出了一个在该系统中实现量子关联的方案.结果表明,系统处于稳态时,由于在腔场、量子阱内的激子和运动腔镜之间的纠缠共享,系统将出现三体和两体连续变量纠缠.与以往的文献相比,本文的意义在于由于驱动杂化光力系统的光为中红外波段的单色光,光热力效应可以被安全的忽略.
参考文献:
[1]R. B. Jin, R. Shimizu, F. Kaneda, Y. Mitsumori, H. Kosaka, and K. Edamatsu. Entangled-state generation with an intrinsically pure single-photon source and a weak coherent source[J]. Phys. Rev. A. 2013, 88: 012324.
[2]C. Ospelkaus, U. Warring, Y. Colombe, K. R. Brown, J. M. Amini, D. Leibfried, and D. J. Wineland. Microwave quantum logic gates for trapped ions [J]. Nature (London). 2011, 476: 181-184.
[3]A. J. Berkley, H. Xu, R. C. Ramos, M. A. Gubrud, F. W. Strauch, P. R. Johnson, J. R. Anderson, A. J. Dragt, C. J. Lobb, F. C. Wellstood. Entangled macroscopic quantum states in two superconducting qubits[J]. Science. 2003, 300: 1548-1550.
[4]L. DiCarlo, M. D. Reed, L. Sun, B. R. Johnson, J. M. Chow, J. M. Gambetta, L. Frunzio, S. M. Girvin, M. H. Devoret, and R. J. Schoelkopf. Preparation and measurement of three-qubit entanglement in a superconducting circuit[J]. Nature. 2010, 467: 574-578.
[5]D. Vitali, S. Gigan, A. Ferreira, H. R. Bohm, P. Tombesi, A. Guerreiro, V. Vedral, A. Zeilinger, and M. Aspelmeyer. Optomechanical entanglement between a movable mirror and a cavity field[J]. Phys. Rev. Lett. 2007, 98: 030405.
[6]M. Abdi and A. R. Bahrampour. Improving the optomechanical entanglement and cooling by photothermal force[J]. Phys. Rev. A. 2012, 85: 063839.
[7]A. Farace and V. Giovannetti. Enhancing quantum effects via periodic modulations in optomechanical systems[J]. Phys. Rev. A. 2012, 86: 013820.
[8]J. M. Dobrindt, I. Wilson-Rae, and T. J. Kippenberg. Parametric normal-mode splitting in cavity optomechanics[J]. Phys. Rev. Lett. 2008, 101: 263602.
[9]K. Hammerer, M. Wallquist, C. Genes, M. Ludwig, F. Marquardt, P. Treutlein, P. Zoller, J. Ye, and H. J. Kimble. Strong coupling of a mechanical oscillator and a single atom[J]. Phys. Rev. Lett. 2009, 103: 063005.
[10]S. Camerer, M. Korppi, A. Jockel, D. Hunger, T. W. Hansch, and P. Treutlein. Realization of an optomechanical interface between ultracold atoms and a membrane[J]. Phys. Rev. Lett. 2011, 107: 223001.
[11]C. Genes, D. Vitali, and P. Tombesi. Emergence of atom-light-mirror entanglement inside an optical cavity[J]. Phys. Rev. A. 2008, 77: 050307(R).
[12]B. Rogers, M. Paternostro, G. M. Palma, and G. De Chiara. Entanglement control in hybrid optomechanical systems[J]. Phys. Rev. A. 2012, 86: 042323.
[13]Sh. Barzanjeh, D. Vitali, P. Tombesi, and G. J. Milburn. Entangling optical and microwave cavity modes by means of a nanomechanical resonator[J]. Phys. Rev. A. 2011, 84: 042342.
[14]V. Giovannetti and D. Vitali. Phase-noise measurement in a cavity with a movable mirror undergoing quantum Brownian motion[J]. Phys. Rev. A. 2001, 63: 023812.
[15]Eyob A. Sete and H. Eleuch. Controllable nonlinear effects in an optomechanical resonator containing a quantum well[J]. Phys. Rev. A. 2012, 85: 043824.
[16]E. X. DeJesus and C. Kaufman. Routh-Hurwitz criterion in the examination of eigenvalues of a system of nonlinear ordinary differential equations[J]. Phys. Rev. A. 1987, 35: 5288.
[17]S. Mancini, D. Vitali, and P. Tombesi. Scheme for teleportation of quantum states onto a mechanical resonator[J]. Phys. Rev. Lett. 2003, 90: 137901.
[18]G. Vidal and R. F. Werner. Computable measure of entanglement[J]. Phys. Rev. A. 2002, 65: 032314.
(责任编辑:王海波)

