“四化”提高数学复习效率

程鹏

中考数学总复习应达到以下目的：使所学知识系统化、结构化、让学生将初中三年的数学知识连成一个有机整体，更利于学生理解；通过经典习题，巩固数学思想方法和基本解题技能；做好综合题训练，提高学生综合运用知识分析问题的能力。但是，总复习阶段超量的练习，又会使学生大脑活动由兴奋转向抑制，与高效课堂背道而驰。那么，如何遵循教学规律和学生的认知规律，进行有效的复习呢？结合个人教学实践，笔者认为复习要致力于将知识转化、变化、优化和类化。

一、单元复习———善于“转化”

进行单元复习，通常是按照顺序把概念、公理、定理、公式、法则和性质等机械地复述一遍，这种“炒冷饭”式的复习往往会使学生感到乏味、头绪不清。针对这个问题，笔者采用了单元知识归类编码法：首先列出需要复习的主要知识点，将其归类排队，再进行数字编码。教会学生把知识由厚变薄，增强学生思维的集敛性与概括性。

例如复习《整式》这一单元，笔者将主要知识浓缩为“一、二、三、四、五”：一个中心：整式的化简与求值。两个公式：平方差公式、完全平方公式。三大内容：整式的加减、整式的乘除、因式分解。四个性质：同底数幂的乘法性质、幂的乘方性质、积的乘方性质和同底数幂的除法性质。五个法则：单项式乘以单项式的法则、单项式乘以多项式的法则、多项式乘以多项式的法则、单项式除以单项式的法则、多项式除以单项式的法则。然后，再引导学生按以上提纲找答案，实现知识由薄向厚的转化，收到了良好的复习效果。

二、例题讲解———善于变化

复习课的例题应选择最有代表性、能突出教材重点、反映“课标”基本要求的题目，注意发挥例题以点带面的功能，并且有意识地对例题进行变化，挖掘问题的内涵和外延，提高思维的深度与广阔性，培养学生随问题变化而变化的应变能力。变化的基本方法有：变解题方法，训练发散思维；对例题和习题进行变化，作出类比、推广或引申；题型变化：封闭性变为开放性，证明题变为计算题等；变问题情境、变图形位置、变数、变符号等。

例如，复习《直线和圆的位置关系》时，笔者举了一例：如图1，AB是⊙O的直径，AC是弦，AD和过点C的切线MN互相垂直，垂足为D，求证：AC平分[∠]DAB。

变式四：变“封闭式习题”为“开放式习题”。

如图3，把例题中⊙O的切线MN向上平移，与⊙O交于C、E两点，连接AE，其他条件不变，此时与∠CAD相等的角是哪一个？请说明理由。

如图4，⊙O的直径AB垂直于弦CD，垂足为E，过点C作⊙O的切线交BA的延长线于点P，连接PD。根据以上条件，你能得到哪些结论（至少写出10个）。

这样，通过“变中抓不变”的变式训练，使一道题变成了一串题。这样做可以构建起以原命题为核心的思维单元，不仅有利于学生更加直接触及到数学问题的实质，防止思维定势的负迁移，还对提高学生的观察分析能力和应变能力，拓宽学生的解题思路，形成准确的解题技能大有裨益。

三、解题思路———善于“优化”

训练中，教师不能局限于单一的习惯性思维方式，应结合具体问题不失时机地培养学生从多角度观察、分析问题的能力，有意识地寻求多种途径探讨同一问题，然后进行归纳比较，提炼出最佳解法，使学生在熟练掌握常规方法的基础上有所创新，以达到优化解题思路，培养学生发散性思维和创造性思维能力的目的。

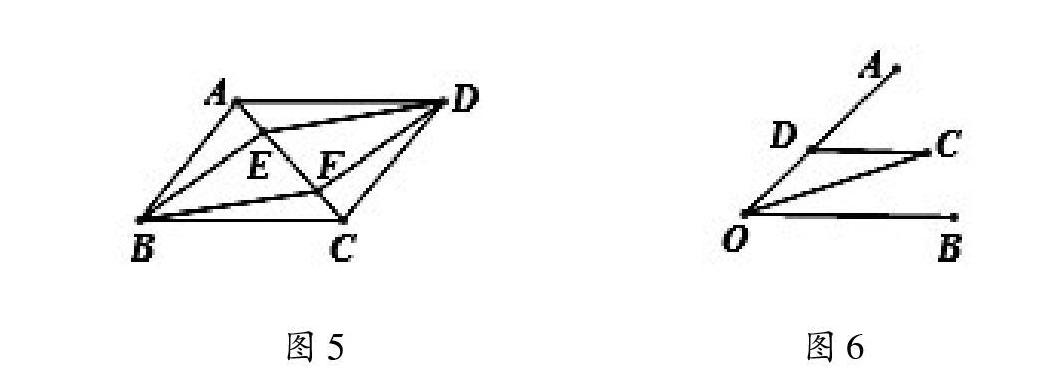
例如，复习《平行四边形》时，笔者举了一例：如图5，E、F是平行四边形ABCD的对角线AC上的两点，且AE=CF，求证：四边形BFDE是平行四边形。

这是人教版八年级下册数学教材第46页的一道例题，学生得出以下三种解法：

思路1：（证两组对边分别相等）先证△ABE≌△CDF得BE=DF，再证ADE△≌△CBF得DE=BF，所以四边形BFDE是平行四边形。__________________

思路2：（证一组对边平行且相等）先证△ADE≌△CBF得DE=BF，∠AED=∠CFB，于是∠DEF=∠BFE，DE∥BF，所以四边形BFDE是平行四边形。

思路3：（证两条对角线互相平分）连接BD，交AC于O，由平行四边形ABCD得AO=CO，BO=DO，因为AE=CF，所以AO-AE=CO-CF，即EO=FO，所以四边形BFDE是平行四边形。

这三种解法分别用到了平行四边形的三种不同的判定方法，沟通了知识之间的内在联系，通过观察和联想，产生思维的飞跃，获得崭新而巧妙的最佳解题途径——第三种解法，有利于提高学生的解题水平，优化思维品质。

四、习题归纳———善于“类化”

在复习中，教师要善于引导学生将习题归纳成类，集中力量解决同类题中的典型问题，总结出解这一类问题的方法和规律，并以此为契机构建思维单元，不仅可以使学生平时所学的零散知识系统化，形成良好的知识结构，还可以提高学生思维的深度与广阔性，实现打造高效课堂、减轻学生负担的目的。一般可让学生从两方面归类：一是把那些形式上不同而解题思想方法有相似之处的习题进行归纳类比；二是把那些可用某一道习题的结论进行解答的习题归为一类。

例如，复习《等腰三角形》时，笔者让学生求证：如果三角形一个外角的平分线平行于三角形的一边，那么这个三角形是等腰三角形。

这是人教版八年级上册数学教材第78页的一道例题，解决这道题并不难，学生很快就完成了证明过程。证完之后，笔者引导学生探究问题的本质特点，归纳了一个非常重要的结论：角平分线+平行线→等腰三角形，图6是这个结论的基本图形。接着，笔者发动学生从教材和有关资料上找出了下面一组含有基本图形的相关习题。

1.在△ABC中，CE平分∠ACB交AB于E，EF∥BC交AC于O，交外角∠ACD的平分线于F，求证：O为EF的中点。

2.已知AD是钝角△ABC的角平分线，DE∥AC交AB于E，EF⊥AD交BC的延长线于F，求证：∠B=∠CAF。

3.已知AD是锐角△ABC的角平分线，BE⊥AD交AD的延长线于E，EF∥AC交AB于F，求证：AF=FB。

4.在四边形ABCD中，AB∥DC，E是DC的中点，且AE平分∠BAD，延长AE、BC交于点F，求证：AB=AD+BC。

上面几道题，虽然题设和结论均不相同，但都可用基本题的结论给出简捷的解答。这就以基本题为中心，构成一个思维单元，使学生在处理“角平分线+平行线”的一类几何题时都能迅速地解答，达到了“会一类”的效果。经常进行这样的归类训练，不仅能使学生把已掌握的结论或解题技能从一个题迁移到另一个题，同时对于培养学生良好的思维品质、发展思维能力也有十分重要的意义。

（作者单位：谷城县城关中心学校）

实习编辑 孙爱蓉

责任编辑 刘玉琴