BLOW-UP OF CLASSICAL SOLUTIONS TO THE COMPRESSIBLE MAGNETOHYDRODYNAMIC EQUATIONS WITH VACUUM∗

Shengguo ZHU(朱圣国)Department of Mathematics,Shanghai Jiao Tong University,Shanghai 200240,China; School of Mathematics,Georgia Tech Atlanta 30332,USA



BLOW-UP OF CLASSICAL SOLUTIONS TO THE COMPRESSIBLE MAGNETOHYDRODYNAMIC EQUATIONS WITH VACUUM∗

Shengguo ZHU(朱圣国)
Department of Mathematics,Shanghai Jiao Tong University,Shanghai 200240,China; School of Mathematics,Georgia Tech Atlanta 30332,USA

E-mail:zhushengguo@sjtu.edu.cn

AbstractIn this paper,we consider the formation of singularity for the classical solutions to compressible MHD equations without thermal conductivity or in finity electric conductivity when the initial data contains vacuum.We show that the life span of any smooth solution will not be extended to∞,if the initial vacuum only appears in some local domain and the magnetic field vanishes on the interface that separates the vacuum and non-vacuum state,regardless the size of the initial data or the far field state.

Key wordsMHD;in finity electric conductivity;classical solutions;vacuum;blow-up

2010 MR Subject Classi fi cation35A09;35B44;35M31;35Q31;35Q35;35Q85

∗Received September 29,2014;revised January 11,2015.The research was supported in part by National Natural Science Foundation of China(11231006),Natural Science Foundation of Shanghai(14ZR1423100)and China Scholarship Council.

1 Introduction

Magnetohydrodynamics is that part of the mechanics of continuous media which studies the motion of electrically conducting media in the presence of a magnetic field.The dynamic motion of fl uid and magnetic field interact strongly on each other,so the hydrodynamic and electrodynamic effects are coupled.The applications of magnetohydrodynamics cover a very wide range of physical objects,from liquid metals to cosmic plasmas,for example,the intensely heated and ionized fluids in an electromagnetic field in astrophysics,geophysics,high-speed aerodynamics,and plasma physics.In 3-D space,the compressible magnetohydrodynamic equations(MHD)in a domain Ω⊂R3can be written as

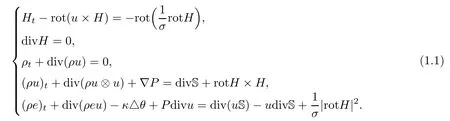
The initial data is given by

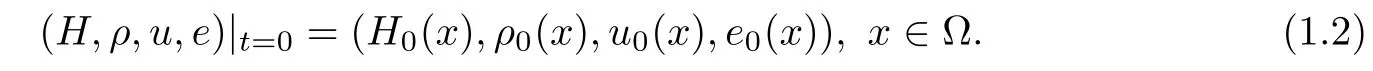
In this system,Ω⊂R3is a smooth domain;x∈Ω is the spatial coordinate;t≥0 is the time;H=(H1,H2,H3)⊤is the magnetic field;0＜σ≤∞is the electric conductivity coeffi cient;ρ is the mass density;u=(u1,u2,u3)⊤∈R3is the velocity of fluids;e is the speci fi c internal energy;κ≥0 is the thermal conductivity coeffi cient;S is the viscosity stress tensor given by

where I3is the 3×3 unit matrix,µis the shear viscosity coeffi cient,is the bulk viscosity coeffi cient,µand λ are both real constants.

We only study the ideal polytropic fluids,so that P,e and θ are given by

where θ is the absolute temperature,R and cvare both positive constants,γ is the adiabatic index satisfying

Although the electric field E doesn’t appear in system(1.1),it is indeed induced according to a relation

by moving the conductive fl ow in the magnetic field.

In the case that the domain Ω has boundary,the standard no-slip boundary condition or Navier-slip boundary condition will be supplemented.

In this paper,it will be always assumed that

When H≡0 in 3-D space,the existence of unique local strong(or classical)solution with vacuum has been solved by many papers,and we refer the readers to[1,2].Huang-Li-Xin obtained the well-posedness of classical solutions with small energy but possibly large oscillations and vacuum for Cauchy problem in[7].Some similar existence results was obtained for compressible MHD equations in[5,8].

The finite time blow-up for the classical solutions with compactly supported initial density to compressible non-isentropic Navier-Stokes equations without thermal conductivity was proved in Xin[15],which was generalized by Cho-Kim[3]to the case of κ＞0.Luo-Xin[12]proved the finite time blow-up of symmetric smooth solutions to two dimensional isentropic Navier-Stokes equations and analyzed the blow-up behavior at in finity time for one point vacuum initial data.Du-Li-Zhang[4]showed the finite time blow-up of smooth solutions to the isothermal case for the one dimensional case and two dimensional case with spherically symmetric assumptions.

If we remove the key assumption that the initial mass density is compactly supported,the finite time blow-up was proved in Rozanova[14]for classical solutions to compressible noisentropic fl ow with highly decreasing at in finity.For the compressible isentroic Navier-Stokes or MHD equation in 3-D space,it can be shown in[13]as follows:

Theorem 1.1(see[13])Assume thatif the momentumthen there exists no global classical solution with conserved mass,momentum and total energy.

From the blow-up results mentioned above,the vacuum far fields seems a necessary assumption on the formation of singularities for both isentropic fl ow and non-isentropic fl ow.However,recently,via an accurate study on the behavior of fluids’velocity in the vacuum domain,Xin-Yan[16]showed that if the initial vacuum only appears in some local domain,the smooth solution(ρ,u,θ)to the Cauchy problem(1.1)-(1.2)with H≡0 and κ≡0 will blow-up in finite time regardless of the size of initial data,which removed the key assumption that the vacuum must appear in the far field in[15].

So,it is interesting to ask that whether the similar phenomenon still happens for the corresponding MHD equations.Compared with[16],due to the appearance of electromagnetic momentum fl ux density tensor

in the momentum equations(1.1)4,it is not easy to see that the momentum(see P∗(t)in(2.19))of the fl uid in the domain that we considered is still conserved,which plays an essential role in the proof of[16].In this paper,based on the framework laid out in[16]with extra attention to the behavior of the magnetic fi led H in the vacuum domain,we answered this question positively.

Before stating our main results,we need to give some related de finitions.The first one is the classical solution that we considered in this paper:

De finition 1.2(Classical solutions)Let Tbe positive.(H(t,x),ρ(t,x),u(t,x),e(t,x))is called a classical solution to the compressible MHD equations(1.1)on(0,T)×Ω if

and satisfies equations(1.1)point-wisely on(0,T)×Ω.It is called a classical solution to the Cauchy problem(1.1)-(1.2)if it is a classical solution to equations(1.1)on(0,T)×R3and takes on the initial data(1.2)continuously.Similarly,it is called a classical solution to the initial boundary value problem(IBVP)for equations(1.1)if it is a classical solution to equations(1.1),takes the initial data(1.2),and satisfies the boundary conditions continuously.

Remark 1.3For the compressible non-isentropic Navier-Stokes equations without heat conductivity(letting H=0 and κ=0 in(1.1)),the existencee of the unique local strong solution with vacuum in terms of(ρ,u,P)has been proved by Cho-Kim[1],which was extended to the compressible non-isentropic MHD equations without heat conductivity by Fan-Yu[5].However,due to the high degeneracy of this system(also compressible MHD equations)in the vacuum domain,the existencee of the unique strong or classical solution in terms of(ρ,u,θ)or(ρ,u,e)with vacuum is still an open open problem until now.The essential difficulty is that we could not sucessfully find any structure or equation to control the behavior of θ or e when mass density vanishes.Hence it is difficult to get uniform estimates for the velocity or temperature near vacuum.Our result shown in the following Theorem 1.2 and[14]show that the classical solutions of the corresponding systems will not exist globally at least.The further research onthe possible instantaneous blow-up of the classical solutions is now in progress,which means that maybe these systems even could not support a smooth solution for any positive time due to the high degeneracy caused by vacuum.

Second we give the de finition of the isolated mass group which is firstly introduced in[16]for compressible Navier-Stokes equations.

De finition 1.4(Isolated mass group)We say(H0(x),ρ0(x),u0(x),e0(x))has an isolated mass group,if there are two bounded open sets A0⊂R3and B0⊂R3such that B0is connected,and

for some positive constant R0,where BR0is the ball centered at the origin with radius R0.

Then based on the above de finitions,we have the following blow-up result.

Theorem 1.5We assume that(H0(x),ρ0(x),u0(x),e0(x))has an isolated mass group(A0,B0).Let(H,ρ,u,e)on[0,T]×R3be a classical solution of Cauchy problem(1.1)-(1.2),then it will blow up in finite time,i.e.,

Moreover,Theorem 1.5 can be extended to the initial boundary value problem in a smooth and bounded domain Ω⊆R3under some suitable boundary condition(such as(H,u)|∂Ω=0).In order to show this conclusion precisely,we need to introduce the following physical quantities over domain A0:

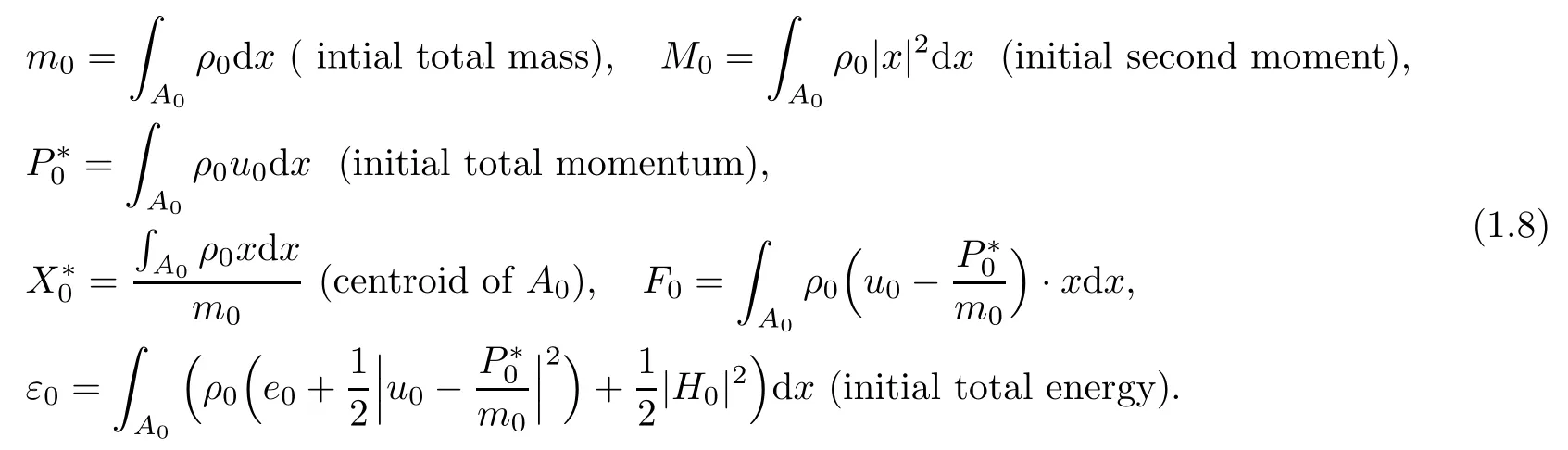
Denote by T0the unique positive root of the following equation

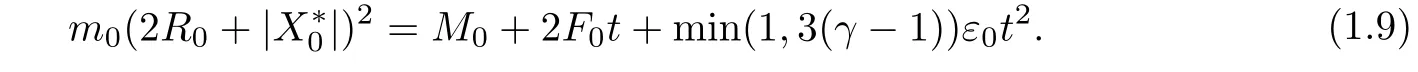
Let cl(A)be the closed convex hull of A.

Theorem 1.6We assume that(H0(x),ρ0(x),u0(x),e0(x))has an isolated mass group(A0,B0),and assume further that

Remark 1.7Theorem 1.6 holds independently of the boundary conditions on∂Ω.

Remark 1.8Theorem 1.5 shows that any classical solution to the compressible MHD system without heat conductivity will blow up in finite time,as long as its initial data has an isolated mass group(A0,B0),regardless the size of the initial data or the far field state.

Remark 1.9From the arguments used in[3,15,16],for classical solutions to the compressible MHD equations(1.1)with κ=0,it holds that in the vacuum domain,

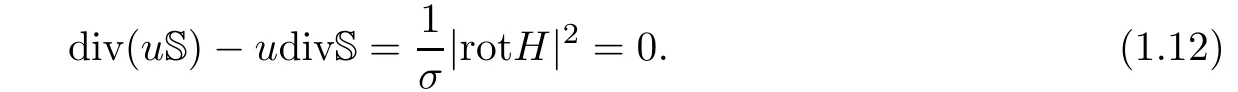
It follows from(2.7)and(1.5)that in the vacuum domain:

When H≡0,an important observation for the beahvior of velocity u in the vacuum domain has been shown in[16]:

where N(t)is an antisymmetric matrix.We refer the readers to Liu-Yang[10,11]for more discussions.However,for the compressible MHD equations(1.1)with κ=0,we not only show that the velocity u of magnetic fl uid satisfies form(1.14)in the vacuum domain,but also give another important observation on the magnetic field H in the vacuum domain,which can be shown as

According to the proof in Section 2,(1.14)-(1.15)implies that the|H|will not change along the particle parth(see De fi ntion 2.1)in the vacuum domain,which is the key point to make sure that the total momentum of A(t)(see De fi ntion 2.1)is conserved under the assumption H0=0,∀x∈∂A0.Via the similar argument used in[16],the conserved momentum of A(t)leads to the invariance of the centroid of A(t),which is the most important information for the derivation of our finite time blow-up.

The rest of this paper is organized as follows.In Section 2,we first give some important properties of classical solutions if its initial data has an isolated mass group,then we prove the corresponding formation of singularity for Cauchy problem.Finally,in Section 3,we make a discussion for intial boundary value problem with suitable boundary condtions.

2 Finite Time Blow-up for Cauchy Problem

In this section,we will study the finite time blow-up for the classical solution to the Cauchy problem(1.1)-(1.2).Before proving the main blow-up result,we first give some important properties which will be uesd in our proof.

2.1Preliminary

First,in order to consider the evolution of A0and B0as time t goes,we need the following de finition.

De finition 2.1(particle path and fl ow map)Let x(t;x0)be the particle path starting at x0when t=0,i.e.,

Then we can denote by A(t),B(t),B(t)A(t)three regions that are the images of A0,B0,and B0A0respectively under the fl ow map of(2.1),i.e.,

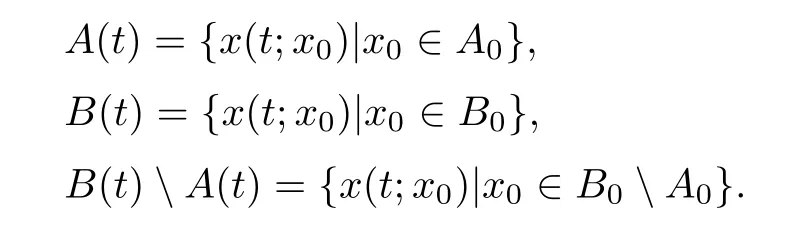
Now we show the behavior of velocity u in the vacuum domain B(t)A(t).

Lemma 2.2We assume that(H0(x),ρ0(x),u0(x),e0(x))has an isolated mass group(A0,B0).Then for the classical solution(H,ρ,u,e)on[0,T]×R3of the Cauchy problem(1.1)-(1.2),there exists an antisymmetric matrix N(t)and a vector b(t)such that

and

Moreover,we also have rotH(t,x)=0,∀x∈B(t)A(t),when 0＜σ＜+∞.

ProofFirst,from the energy equation(1.1)5:

we immediately have

Due to

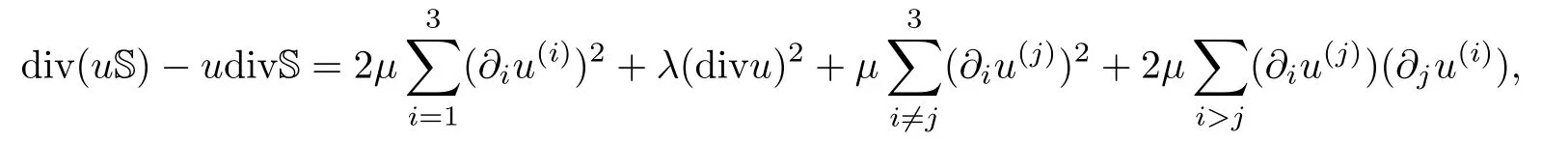
when λ≤0,according to the Cauchy inequality,we have

when λ≥0,it is clear to see that

which together with(2.4)implies that

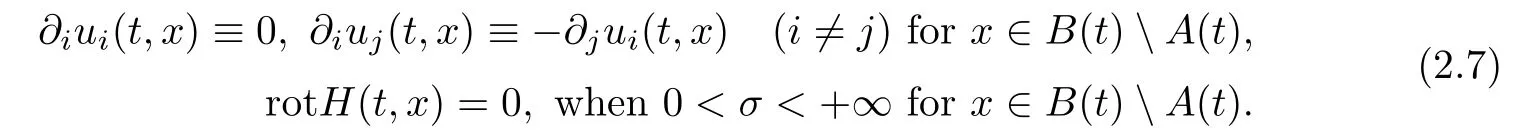
From direct calculations,we have

which means that

So there exists a matrix N(t)and a vector b(t)such that

Due to(2.7),we have

So N(t)is an antisymmetric matrix.Then we can quickly get the second relation shown in(2.2):

Finally,we will prove(2.3).By direct calculation,we have

The following lemma will show that the volume of A(t)will not change as time goes.

Lemma 2.3We assume that(H0(x),ρ0(x),u0(x),e0(x))has an isolated mass group(A0,B0).Then for the classical solution(H,ρ,u,e)on[0,T]×R3of the Cauchy problem(1.1)-(1.2),we have

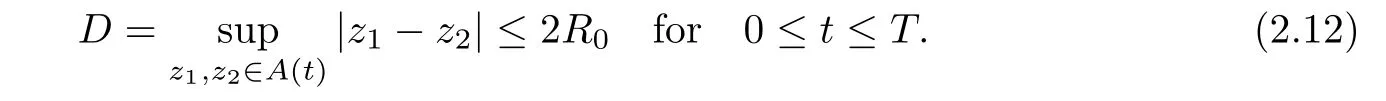
ProofAccording to Lemma 2.2,we know that

Then for any two points zi(t;αi)(i=1,2),we have

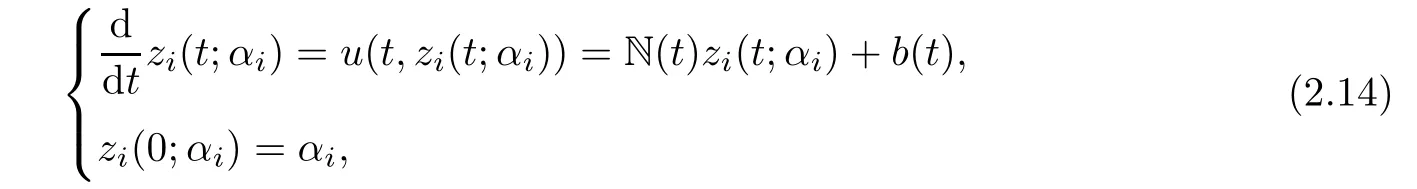
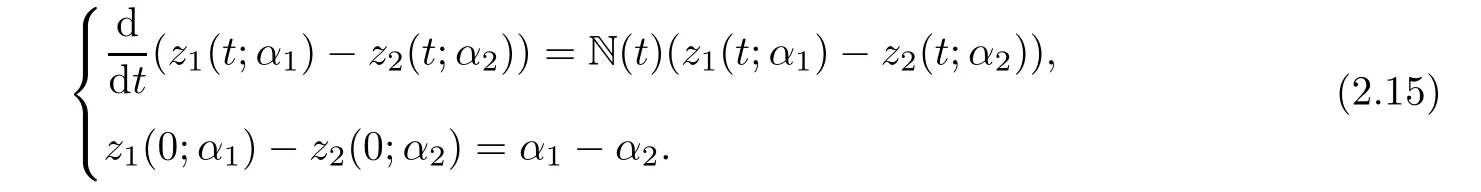
Since N(t)is antisymmetric,we have

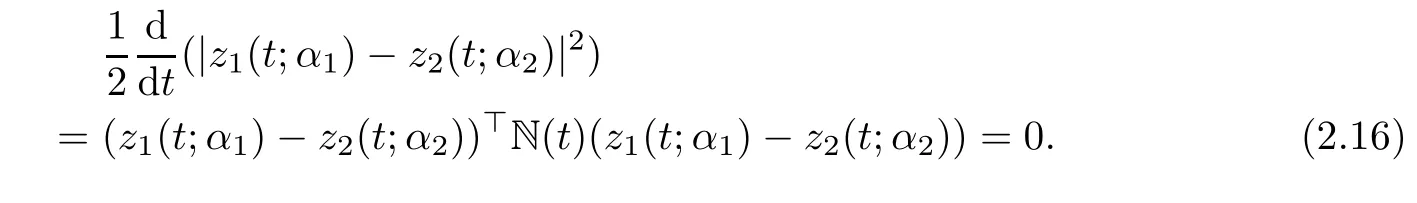
That is to say

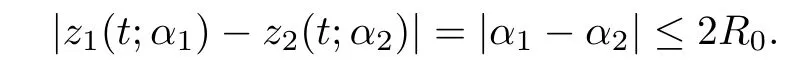
Based on the behavior of the velocity u in the vacuum domain,we will give a very interesting observation on the magnetohydrodynamic field H,which will make sure that the total momentum of the fl uid in A(t)is conserved.

Lemma 2.4We assume that(H0(x),ρ0(x),u0(x),e0(x))has an isolated mass group(A0,B0).Then for the classical solution(H,ρ,u,e)on[0,T]×R3of the Cauchy problem(1.1)-(1.2),we have

ProofDue to the proof of Lemma 2.2,we know that

According to the formula

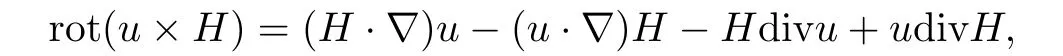
we have

which,together with(2.10),implies that

From the above relation,it is not difficult to show that

which means that

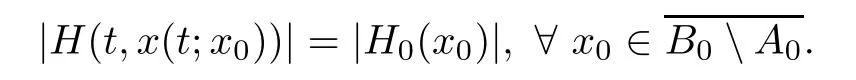
Though Lemma 2.3 means that the volume of A(t)is invariant,however,we have to point out that the vacuum boundary∂A(t)varies as time goes.In order to deal with this case,we need to introduce the well known Reynolds transport theorem[6]:

Lemma 2.5For any Q(t,x)∈C1(R+×R3)we have

where n is the outward unit normal vector to∂A(t),and u is the velocity of the fl uid.

For the need of our proof,we introduce the following physical quantities over domain A(t):

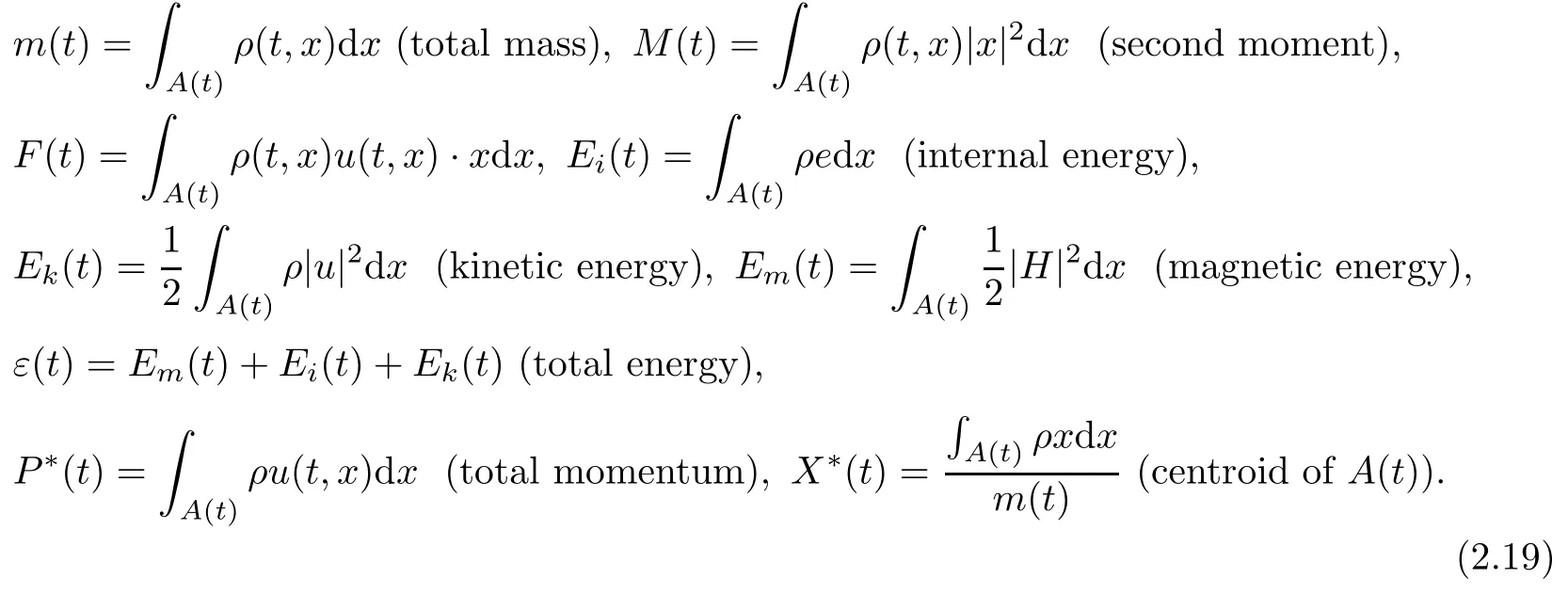
Now we will show the conservations of the total mass,total momentum,total energy and the invariance of the centroid of A(t).

ProofFirst,according to the continuity equation and Lemma 2.5,we easily have

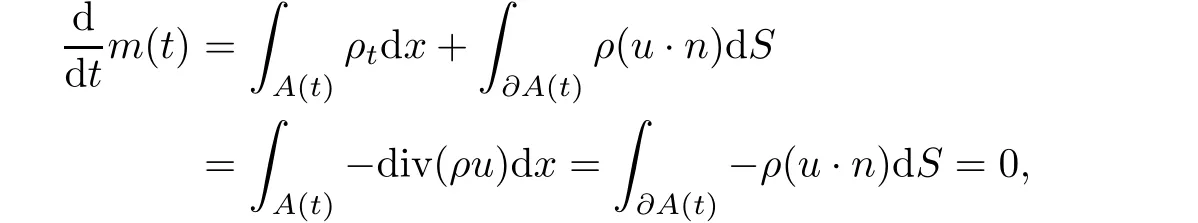
which implies that m(t)=m0.

Second,according to the momentum equations,Lemma 2.5,and

we have

According to Lemma 2.4,we have

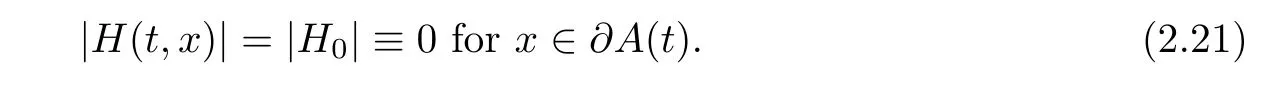
Combining(2.20)and(2.21),we obtain the desired conclusion that

Next,according to the energy equation,we quickly have the following relation

Then from Lemma 2.5,(2.21)and(2.22),we have

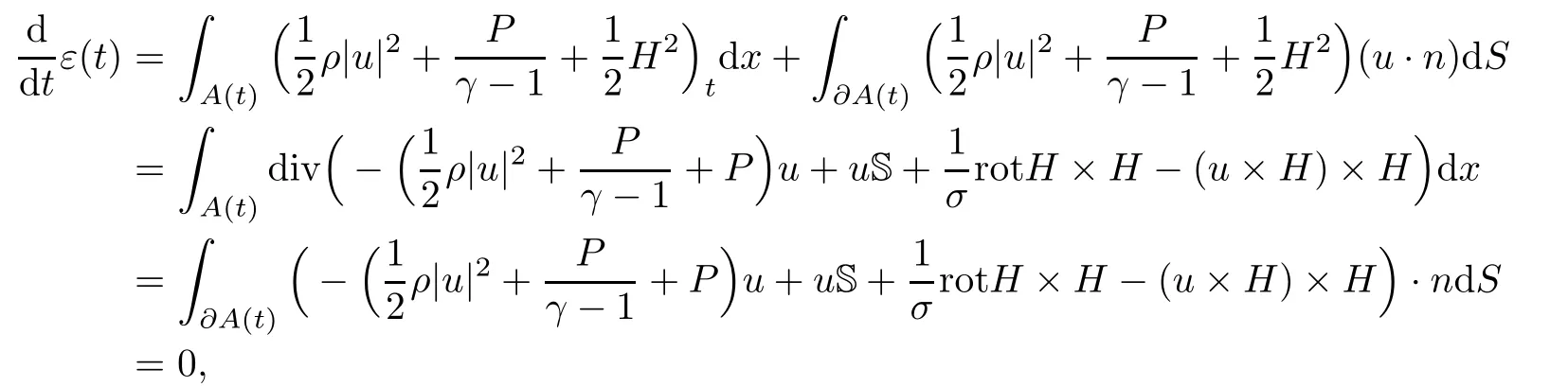
which means that ε(t)=ε0.

Finally,from the de finition of X∗(t),m(t)=m0andwe have

Moreover,since the total mass on A(t)is conserved,thusis contained in the closed convex hull of A(t)fromwe easily know that

2.2Proof of Theorem 1.5

Based on the conclusions obtained in Lemmas 2.2-2.6,we give the proof for Theorem 1.5.

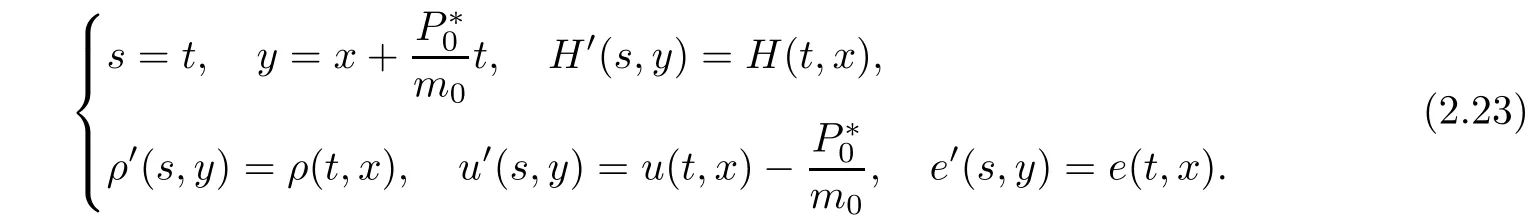
Equations(1.1)and the initial assumption(1.6)are invariant under this transformation.So,without loss of generality,we can assume that

From the continuity equation and integration by parts,we get

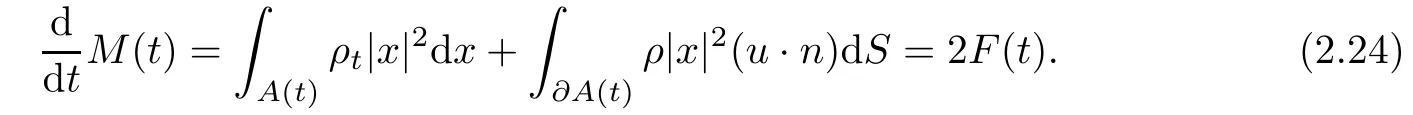
From Lemma 2.2,the momentum equations and integration by parts,we also get

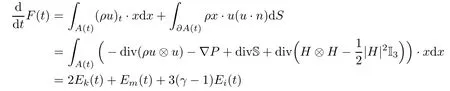
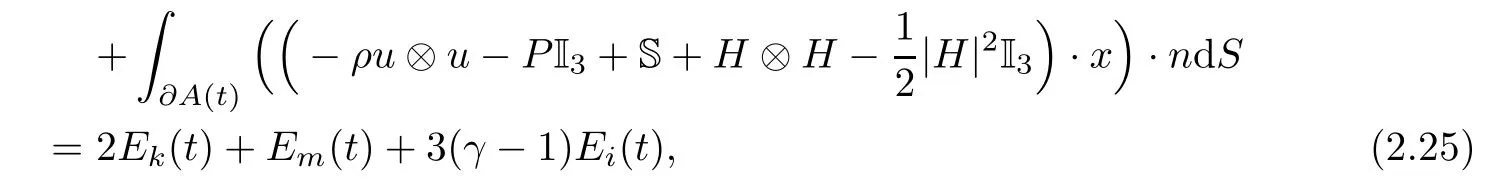
which means that

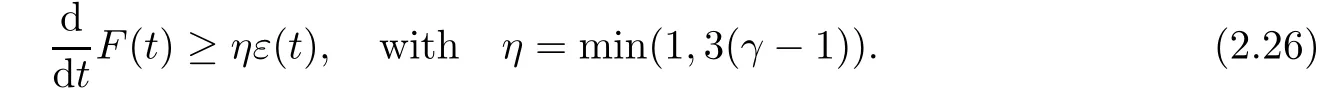
Integrating(2.24)and(2.26)over[0,t],respectively,we obtain

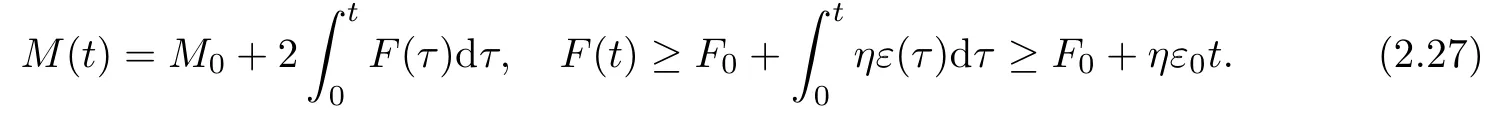
Then we have

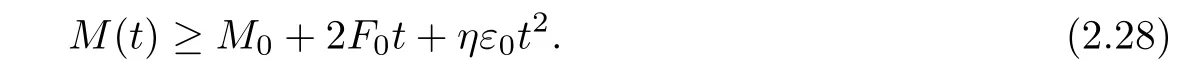
According to Lemma 2.6,it yields

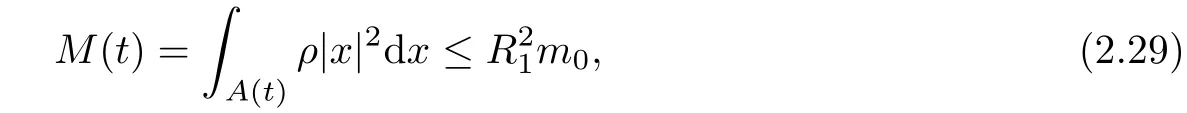
Combining(2.28)with(2.29),we have

which means that T＜+∞.

3 Finite Time Blow-Up for IBVP

In this section,we extend the blow-up results obtained in Section 2 to some initial boundary value problem under some suitable boundary condition.

ProofFirst,the key point of this proof is to make sure that the imagine B(t)of B0under the fl ow map(2.1)cannot reach the boundary of Ω.Then we can use the same arguments for Cauchy problem as in Lemmas 2.2-2.6 and Theorem 1.5 to get the corresponding blow-up result for the initial boundary value problem.Consider the case

Step 1We claim that if T∗exists,then there exists a positive lower bound∈＞0 such that T∗≥∈.In fact,without loss of generality,we assume that T＞1.Then from the de finition of particle path x(t;x0),we have

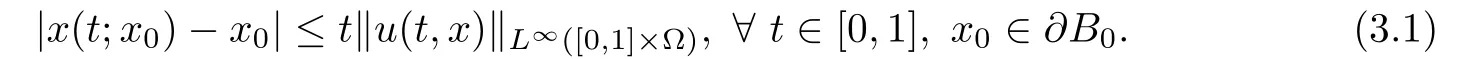
If we let T∗∈(0,1]be small enough such that

then we know that

Then we get that T∗≥∈=T∗＞0.

Step 2We claim that T∗does not exist.In fact,if there exists a T∗,∈≤T∗≤T,due to the de finition of T∗,we have

Then,via the same analysis as in Lemma 2.6,we have

which contradicts with the de finition of T∗.

Step 3Now we show that the life span T of classical solutions is finite,T＜+∞.From Step 2,we know that

Using the same analysis in Lemma 2.6 again,we have

Therefore,we can prove the singualrity formation for the initial boundary value problem from the same arguments as in the proof of Theorem 1.5.

Finally,we consider the casewe have to make the following Galileo transformation,

Equations(1.1),the initial assumption(1.6)and(1.8)are invariant under this transformation.Here the boundary of the domain∂Ω(t)becomes unsteady with the constant velocity

In this case,the de fi ntion of T becomes

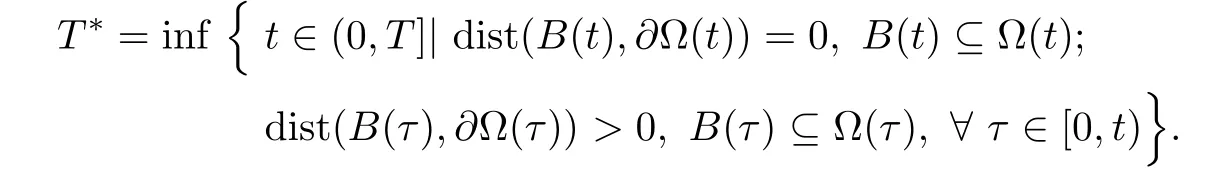
Due to

it is clear that we can prove this T∗does not exist.Then the proof of this case is the same as the Cauchy problem.

References

[1]Cho Y,Kim H.Existence results for viscous polytropic fluids with vacuum.J Di ff er Equ,2006,228:377-411

[2]Cho Y,Kim H.On classical solutions of the compressible Navier-Stokes equations with nonnegative initial densities.Manu Math,2006,120:91-129

[3]Cho Y,Jin B.Blow-up of viscous heat-conducting compressible flows.J Math Anal Appl,2006,320:819-826

[4]Du D,Li J,Zhang K.Blowup of smooth solutions to the Navier-Stokes equations for compressible isothermal fluids.http://arxiv.org/abs/1108.1613v1[math.Ap],2011

[5]Fan J,Yu W.Strong solutions to the magnetohydrodynamic equations with vacuum.Nonlinear Analysis:Real World Applications,2009,10:392-409

[6]Gao D,Liu T.Advanced Fluid Mechanics(in Chinese).Wuhan:Huazhong University of Science and Technology,2004

[7]Huang X,Li J,Xin Z.Global Well-posedness of classical solutions with large oscillations and vacuum.Comm Pure Appl Math,2012,65:549-585

[8]Li H,Xu X,Zhang J.Global classical solutions to the 3D compressible magnetohdrodynamic equations with large oscillations and vacuum.SIAM J Math Anal,2013,45:1356-1387

[9]Li X,Su N,Wang D.Local strong solution to the compressible magnetohydrodynamics fl ow with large data.J Hyper Di ff Equa,2011,3:415-436

[10]Liu T,Yang T.Compressible fl ow with vacuum and physical singularity.Methods Appl Anal,2000,7:495-510

[11]Liu T,Yang T.Compressible Euler equations with vacuum.J Di ff er Equ,1997,140:223-237

[12]Luo Z,Xin Z.Global well-posedness and blowup behavior of classical solutions with large oscil-lations and vacuum to the two-dimensional isentropic compressible Navier-Stokes equations.preprint,2011

[13]Rozanova O.Blow up of smooth solutions to the barotropic compressible magnetohydrodynamic equations with finite mass and energy.Proc Sympos Appl Math,2009,67:911-917

[14]Rozanova O.Blow-up of smooth highly decreasing at in finity solutions to the compressible Navier-Stokes Equations.J Di ff er Equ,2008,245:1762-1774

[15]Xin Z.Blow-up of smooth solutions to the compressible Navier-Stokes equation with compact density.Commun Pure Appl Math,1998,51:0229-0240

[16]Xin Z,Yan W.On blow-up of classical solutions to the compressible Navier-Stokes equations.Commun Math Phys,2013,321:529-541