EXISTENCE AND UNIQUENESS OF PERIODIC SOLUTIONS FOR GRADIENT SYSTEMS IN FINITE DIMENSIONAL SPACES∗
Sahbi BOUSSANDELFaculté des Sciences de Gabès 6072 Zrig Gabès Cité Riadh Tunisia-Laboratoire EDP et Applications LR03ES04,Tunisia
EXISTENCE AND UNIQUENESS OF PERIODIC SOLUTIONS FOR GRADIENT SYSTEMS IN FINITE DIMENSIONAL SPACES∗
Sahbi BOUSSANDEL
Faculté des Sciences de Gabès 6072 Zrig Gabès Cité Riadh Tunisia-Laboratoire EDP et Applications LR03ES04,Tunisia
E-mail:sahbi.boussandel@yahoo.fr
AbstractThis paper deals with an abstract periodic gradient system in which the gradient is taken with respect to a variable metric.We obtain an existence and uniqueness result via the application of a global inverse theorem.
Key wordsexistence and uniqueness;periodic solutions;gradient systems;global inverse theorem
2010 MR Subject Classi fi cation34K30
∗Received September 25,2014;revised May 16,2015.
1 Introduction
In this paper,we investigate the existence and the uniqueness of solutions for the first order nonlinear periodic differential equation

where E:RN→R is a twice differentiable functional,∇g(t)E denotes the gradient of E with respect to a time-variable inner product〈·,·〉g(t),p≥2 and f∈Lp(0,T;RN).
The periodic boundary value problems were studied intensively in recent years under several assumptions on the functional E.Many methods and tools were used in order to solve these problems,e.g.,fixed point methods,degree theory,variational methods,the upperlower solutions method and perturbation and iterative techniques.We refer the reader to[7,8,11,14,16,18-23,32,34]and the references therein for more details about these methods and for abstract results and their applications.
In this paper,the techniques of the proofs are based on the application of the following global inverse functions theorem.
Theorem 1.1(see[24])Let X and Y be two Banach spaces,and let φ:X→Y be a map.The following assertions are equivalent:
i)φ is a homeomorphism from X into Y,
ii)φ is a local homeomorphism and proper.
Recall that the map φ is proper if φ−1(C)is a compact set in X whenever C is a compact set in Y.
Several authors obtained existence and uniqueness results for boundary value problems using global inversion theorems;see for example[1-3,5,6,9,12,13,15,17,26-30,33,35,36].
In order to apply Theorem 1.1,we reformulate problem(1.1)as an algebraic equation
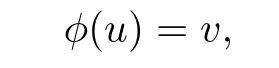
where φ:X→Y is a mapping from a Banach space X into a Banach space Y,and we prove that φ satisfies assumptions of Theorem 1.1.Under some monotonicity condition on the derivative operator E′and under some nondegeneracy condition on g we prove that problem(1.1)admits a unique solution.In the setting of gradient systems in which the gradient is taken with respect to variable metrics,we refer to[10,Theorem 2.10 and Proof of Theorem 6.1-Part 1]in which the metric depends on the space variable,and to[4,Proof of Theorem 4-Part 1]in which the author considered metrics depending on the time and space variables.The problems considered in[4]and[10]are with initial data.
2 Functional Setting and Assumptions
First,we recall from[10]some basic facts and results about Euclidian and Riemannian metrics.Let N∈N∗and let E:RN→R be a Fréchet differentiable functional.We denote by〈·,·〉and‖·‖the Euclidian inner product and norm on RN,respectively.The Euclidian gradient of E is the function∇E which assigns to every point u∈RNthe unique element ∇E(u)∈RNsuch that

By the Riesz-Fréchet theorem,the euclidian gradient∇E is well de fined in the sense that it exists and it is unique.We denote by Inner(RN)the set of all inner products on RN.Let T>0 and let g:[0,T]→Inner(RN)be a function and denote by〈·,·〉g(t)the inner product g(t)at a time t∈[0,T]and by‖·‖g(t)the norm associated with this inner product.For every t∈[0,T],the gradient of E with respect to the inner product〈·,·〉g(t)is the function∇g(t)E which assigns to every point u∈RNthe unique element∇g(t)E(u)∈RNsuch that

By the Riesz-Fréchet theorem,the euclidian gradient∇g(t)E exists and is unique for every t∈[0,T].
For every t∈[0,T],let Q(t)∈L(RN)be de fined by
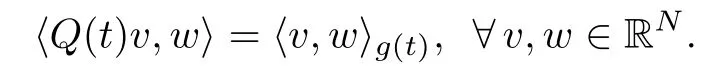
Then we have

Remark 2.1We note that if E is of class C2,we can de fi ne,for every t∈[0,T],the functiongiven for every u∈RNby

where∇2E(u)denotes the Hessian matrix of E at the point u.
We assume that E and g satisfy the following assumptions:
(H1)E∈C2(RN,R),
(H3)∃c′>0,c′′≥0∀u∈RN,〈∇E(u),u〉≥c′‖u‖2−c′′‖u‖,
(H4)for every v,w∈RN,the function t→〈v,w〉g(t)is measurable on[0,T],
(H5)∃c1,c2>0,∀u∈RN,∀t∈[0,T],c1‖u‖≤‖u‖g(t)≤c2‖u‖.
Let p∈[2,∞)and Y=Lp(0,T;RN)which is a Banach space for the norm
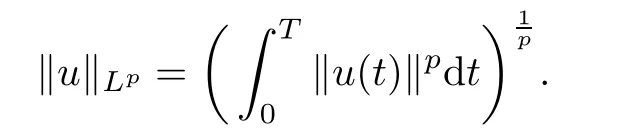
If p=2,then L2(0,T;RN)is a Hilbert space for the inner product

Let further

which is a Banach space for the norm

If p=2,then X is a Hilbert space for the inner product
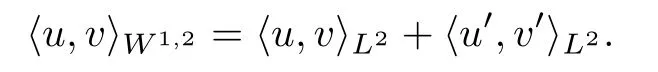
Recall,from the Sobolev embedding theorem,that

with continuous embedding,so that the condition u(0)=u(T)which appears in the de finition of the space X makes sense.
3 Some Preliminary Results
In this section,we give some preliminary lemmas which turn out essential for the proof of the main result.The first one provides a regularity result for the Nemytskii operator associated to the function∇g(·)E.
Lemma 3.1Let

be the Nemytskii operator de fined by

Under assumptions(H1),(H4)and(H5),the Nemytskii operator F is well de fined,continuously differentiable on X and the derivative is given by

ProofLet
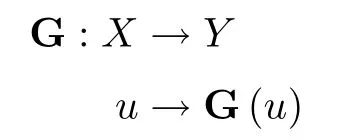
be the Nemytskii operator de fined by

Then we have

The fact that G is continuously differentiable follows similarly as in the proof of[25,Theorem 3.1],and we have
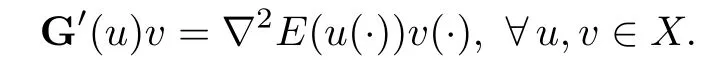
Since,for every t∈[0,T]and every v,w∈RN,〈v,w〉=〈Q(t)−1v,w〉g(t),we deduce from assumption(H5)that

and therefore
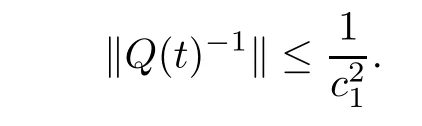
It follows that F is well de fined,continuously differentiable on X,and for every u,v∈X,we have
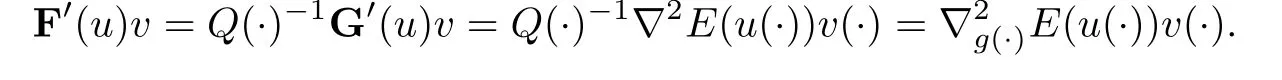
For the second result,we give su ffi cient conditions that ensure the existence and the uniqueness of solutions for a linear nonautonomous problem with periodic boundary condition.
Theorem 3.2Assume that p=2.Let(A(t))t∈[0,T]⊂L(RN)be such that A is measurable on[0,T]and assume that
(a)∃c>0,∀t∈[0,T],∀x∈RN,〈A(t)x,x〉≥c‖x‖2,
Then,for every f∈L2(0,T;RN),there exists a unique u∈W1,2(0,T;RN)which is solution of the nonautonomous linear problem

ProofLet f∈L2(0,T;RN).For every α∈[0,1],we de fi ne the linear operator

where Id is the identity operator on RN,and we consider the linear nonautonomous problem

We introduce the set

For every α∈[0,1],we de fi ne the linear operator Tα:X→Y by

We note,by assumption(b),that Tαis a bounded operator.We note also that α∈M if and only if the operator Tαis invertible.
For α=0,eq.(3.2)is a simple ordinary differential equation which has a unique solution u∈X,and henceWe will show that M is an open and closed set in[0,1].Let us prove that M is an open set in[0,1].This is a consequence of assumption(b)and the Neumann Series.Indeed,by assumption(b),there exists C1>0 such that

where I is the natural embedding from X into Y.Fix an α∈M and denote

Let β∈[0,1]such that

and prove that Tβis invertible.By using(3.3)and(3.4),we have
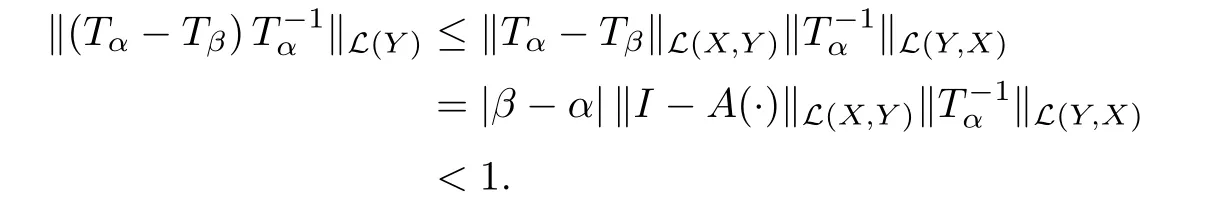
It follows by the Neumann series that the operatoris invertible.However,

Now,we prove that M is a closed set in[0,1].Let(αn)be any sequence in M which converges to α∈[0,1].From the de finition of the set M,for every n∈N,there exists a unique un∈W1,2(0,T;RN)which is solution of

We multiply eq.(3.5)by unwith respect to the inner product of L2(0,T;RN),and we obtain
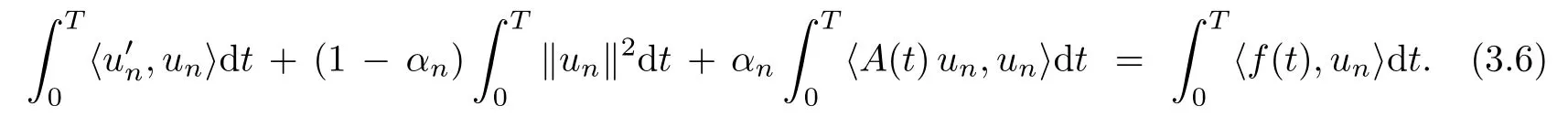
By using the periodic boundary condition un(0)=un(T),we have
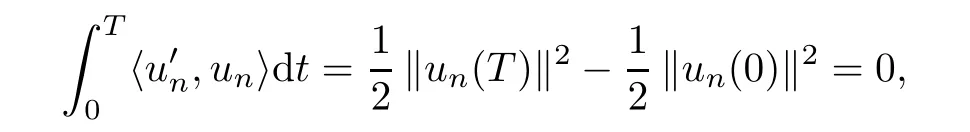
and hence by assumption(a),identity(3.6)implies

Therefore
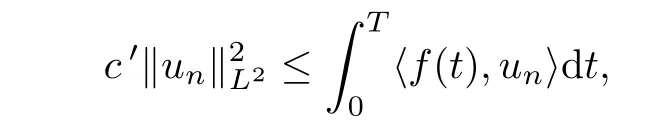
where c′=min(1,c).It follows that

Moreover,by assumption(b)and estimate(3.7),we can deduce from eq.(3.5)that
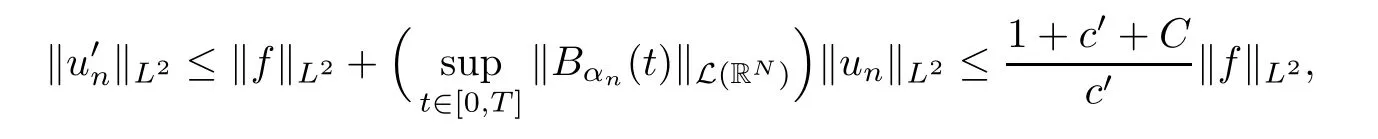
and therefore,by combining this last estimate with estimate(3.7)we obtain

Let h∈X.We use estimate(3.8)in order to obtain

We let n→∞in this last estimate and we obtain

From this last estimate it follows that the operator Tα:X→Y is injective and by[31,Lemma 4.47],Tαhas closed range.By[31,Theorem 4.48],it remains to prove that the operator Tα:X→Y is surjective,that is RanTαis dense in Y.Suppose by contradiction that RanTαY.Then,there exists k∈Y{0}such that for every h∈X we have〈Tαh,k〉L2=0.Since the sequenceis bounded in X,and since X is re fl exive,it therefore admits a weakly convergent subsequence(again denoted bywith some weak limit h∈X.Then

a contradiction to the fact that k0.Hence RanTα=Y,that is Tαis surjective.Since[0,1]is connected,we can deduce that M=[0,1]and the conclusion follows by taking α=1.
4 The Main Result
We consider the following gradient system

The main result of this paper is the following theorem.
Theorem 4.1Let p∈[2,∞).Under assumptions(H1)-(H5),for every f∈Lp(0,T;RN),problem(4.1)admits a unique solution u∈W1,p(0,T;RN).
ProofFor the proof,we apply Theorem 1.1.We study the cases p=2 and p>2 separately.
Case 1p=2.
Let φ:X→Y be the function de fined by

The map L:u→u′is linear and bounded from X into Y,therefore continuously differentiable and we have
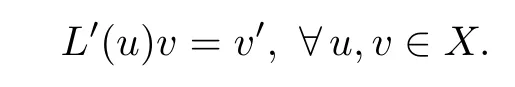
Hence by Lemma 3.1,φ is well de fined,continuously differentiable on X and the derivative of φ is given by

Let u∈X be fixed.We prove that φ′(u)is invertible.This is equivalent to the property that for every e∈L2(0,T;RN),the nonautonomous linear problem

admits a unique solution.Let
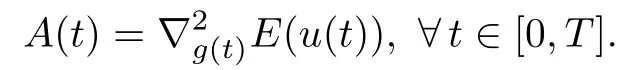
We have for every t∈[0,T],
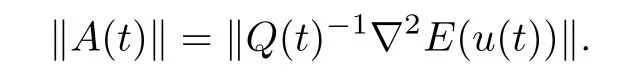
Since,for every t∈[0,T],we have(see the proof of Lemma 3.1),we obtain
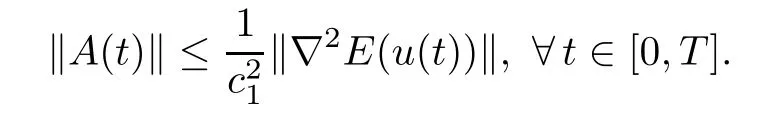
By using the continuous embedding W1,2(0,T;RN)C([0,T];RN),there existssuch that

Since E is of class C2,there existssuch that

and consequently,we obtain

This proves that assumption(b)of Theorem 3.2 is satis fied.Moreover,we have from assumption(H2)

Therefore,as a consequence of Theorem 3.2,problem(4.2)admits a unique solution and thenφ′(u)is a linear homeomorphism from X into Y.Hence,φ is a local homeomorphism.
In order to show that φ is a proper map,let C be any compact set of Y and prove thatφ−1(C)is a compact set of X.Let(un)be any sequence of φ−1(C).Then there exists(vn)a sequence in C such that vn=φ(un)for any n∈N,i.e.,
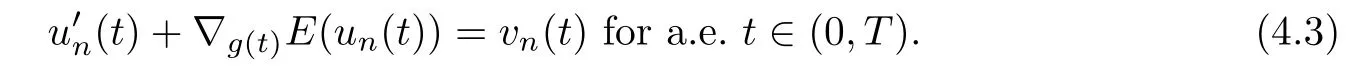
Since C is compact,we can extract from(vn)a subsequence(which we denote again(vn))such that vn→v in C.
By multiplying identity(4.3)bywith respect to the inner product〈·,·〉g(t),then by integrating over the interval(0,T),we have

By using the fact that un(0)=un(T),we have

and hence we obtain

From assumption(H5)we have

and therefore

Since(vn)is bounded inis bounded in L2(0,T;RN)too.By multiplying identity(4.3)by un(t)with respect to the inner product〈·,·〉g(t),then by integrating over the interval(0,T),we have
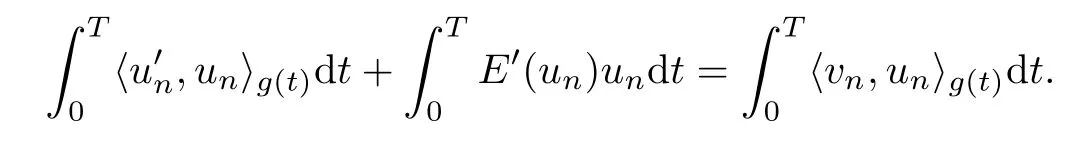
By using assumption(H3),we deduce

This implies that


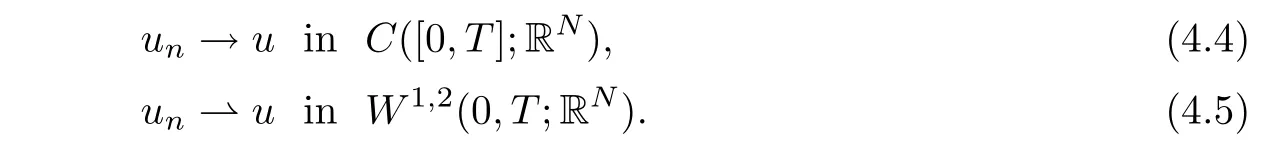
Since∇E is continuous on RN,it follows from convergence(4.4)that∇E(un)→∇E(u)in L2(0,T;RN).Since,for every t∈[0,T],we have∇g(·)E(u)in L2(0,T;RN).From identity(4.3),we deduce thatFrom convergence(4.5),we haveand therefore u′= v−∇g(·)E(u).Hence,un→u in W1,2(0,T;RN),and φ(u)=v∈C.Moreover,we deduce from the fact that un(0)=un(T)and the convergence(4.4)that u(0)=u(T).It follows that un→u in φ−1(C)that is φ−1(C)is a compact set of X.By Theorem 1.1,φ is global homeomorphism from X into Y,and hence problem(4.1)admits a unique solution u∈W1,2(0,T;RN).
Case 2p>2.
We prove that this case is a consequence of Case 1.Let f∈Lp(0,T;RN).Since p>2 we have f∈L2(0,T;RN)and by Case 1,there exists a unique u∈W1,2(0,T;RN)which is solution of problem(4.1).Since W1,2(0,T;RN)is a subspace of C([0,T];RN),the function t→∇E(u(t))is continuous on[0,T]and then∇E(u)∈Lp(0,T;RN).By using the fact that,for every t∈[0,T],we deduce that∇g(·)E(u(·))∈Lp(0,T;RN).It follows from eq.(4.1)that u′∈Lp(0,T;RN).Hence,u∈W1,p(0,T;RN)is the unique solution of problem(4.1).
5 Application
Let E:RN→R be a twice continuously differentiable functional,let ε>0 and m:[0,T]→be a measurable function.We assume that E satisfies the following assumption:
(H)∃c>0,∀u,v∈RN,E′′(u)(v,v)≥c‖v‖2.
Let further g:[0,T]→Inner(RN)be the function de fined by
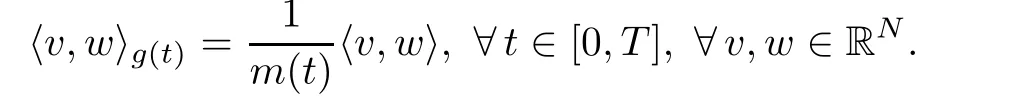
For every t∈[0,T]and every u,v∈RN,we have

Hence,we have
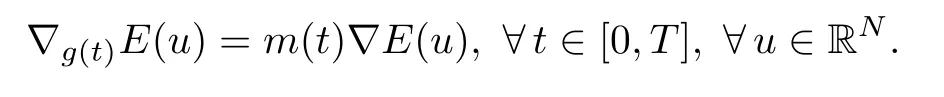
We note that assumption(H2)is equivalent to the following property

It follows that
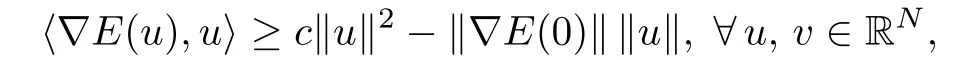
so that assumption(H3)is well satis fied.
It is not difficult to verify that E and g satisfy the other assumptions of Theorem 4.1,so that we obtain the following corollary.
Corollary 5.1Let p∈[2,∞).For every f∈Lp(0,T;RN),there exists a unique u∈W1,p(0,T;RN)which is solution of
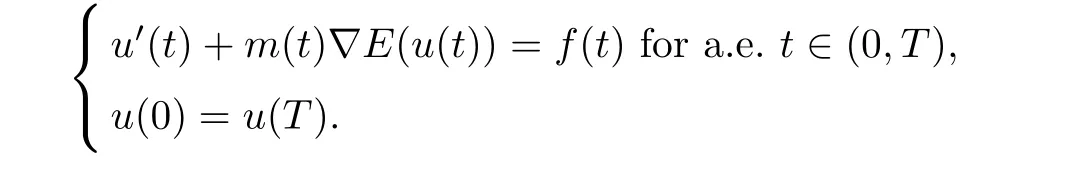
References
[1]Ahmad S.An existence theorem for periodically perturbed conservative systems.Michigan Math J,1973,20:385-392
[2]Amann H.On the unique solvability of semi-linear operator equations in Hilbert spaces.J Math Pures Appl,1982,61:149-175
[3]Amaral L,Pera M.On periodic solutions of nonconservative systems.Nonlinear Anal,1982,6:733-743
[4]Boussandel S.Global existence and maximal regularity of gradient systems.J Di ff er Equ,2011,250(2):929-948
[5]Brown K J.Nonlinear boundary value problems and a global inverse function theorem.Ann Mat Pura Appl,1975,106(4):205-217
[6]Brown K J,Lin S S.Periodically perturbed conservative systems and a global inverse functions theorem.Nonlinear Anal,1980,4:193-201
[7]Capietto A,Mawhin J,Zanolin F.A continuation approach to superlinear periodic boundary value problems.J Di ff er Equ,1990,88:347-395
[8]Chen Y,Chen J,Wan Z.Remarks on the periodic boundary value problems for first-order differential equations.Comput Math Appl,1999,37:49-55
[9]Chen J,O’Regan D.On periodic solutions for even order differential equations.Nonlinear Analysis,2008,69:1138-1144
[10]Chill R,Fasangová E.Gradient systems.In:13th International Internet Seminar
[11]Fonda A Sfecci A.A general method for the existence of periodic solutions of differential systems in the plane.J Di ff er Equ,2012,252:1369-1391
[12]Dalmasso R.An existence and uniqueness theorem for a second order nonlinear system.J Math Anal Appl,2007,327:715-722
[13]Dalmasso R.Unique solvability for a second order nonlinear system via two global inversion theorems.Ele J Di ff er Equ,2008,(11):1-8
[14]Lakshmikantham V,Leela S.Existence and monotone method for periodic solutions of first-oder differential equations.J Math Anal Appl,1983,91:237-243
[15]Lin D,Yang Y Zhu D.Periodic solutions for some ordinary differential equations involving stability.Nonlinear Analysis,2001,45:963-971
[16]Liu Y.Multiple solutions of periodic boundary value problems for first order differential equations.Comput Math Appl,2007,54:1-8
[17]Mawhin J.Contractive mappings and periodically perturbed conservative systems.Arch Math,1976,12:67-73
[18]Mawhin J.Topological Degree Methods in Nonlinear Boundary Value Problems.CBMS-Regional Conf Math 40.Providence,RI:Amer Math Soc,1979
[19]Mawhin J.First order ordinary differential equations with several periodic solutions.J Appl Math Phy(ZAMP),1987,38:257-265
[20]Mawhin J,Thompson H B.Periodic or bounded solutions of Caretéodory systems of ordinary differential equations.J Dyn Di ff er Equ,2003,15(2/3):327-334
[21]Mawhin J.Topological Fixed Point Theory and Nonlinear Di ff erential Equations.Handbook of Topological Fixed Point Theory.Springer,2005
[22]Nagle R K,Sinkala Z.Existence of 2π-periodic solutions for nonlinear systems of first-order ordinary differential equations at resonance.Nonlinear Analysis,TMA,1995,25:l-16
[23]Nieto J J,Alvarez-Noriega N.Periodic boundary value problems for nonlinear first order ordinary differential equations.Acta Math Hungar,1996,71(1/2):49-58
[24]Plastock R.Homeomorphisms between Banach spaces.Trans Amer Math Soc,1974,200:169-183
[25]Rabier P J,Stuart C A.Boundary value problems for first order systems on the half-line.Topol Methods Nonlinear Anal,2005,25(1):101-133
[26]Radulescu M,Radulescu S.Global inversion theorems and applications to differential equations.Nonlinear Analysis,TMA,1980,4(4):951-965
[27]Radulescu M,Radulescu S.An application of Hadamard-Levy theorem to a scalar initial value problem.Proc Amer Math Soc,1989,106(1):139-143
[28]Radulescu M,Radulescu S.An application of a global inversion theorem to a Dirichlet problem for a second order differential equation.Rev Roumaine Math Pures Appl,1992,37:929-933
[29]Radulescu M,Radulescu S.Applications of a global inversion theorem to unique solvability of second order Dirichlet problems.An Univ Craiova,Math Comp Sci Ser,2003,30(1):198-203
[30]Radulescu M,Radulescu S.Global inversion theorems and applications to unique solvability of boundary value theorems for differential equations.Int J Di ff er Equ Appl,2000,1(2):159-166
[31]Rynne B P,Youngson M A.Linear Functional Analysis.Springer Undergraduate Mathematics Series.Springer,2008
[32]Tisdell C C.Existence of solutions to first-order periodic boundary value problems.J Math Anal Appl,2006,323:1325-1332
[33]Trif T.Unique solvability of certain nonlinear boundary value problems via a global inversion theorem of Hadamard-Levy type.Demonstratio Math,2005,38(2):331-340
[34]Vidossich G.Multiple periodic solutions for first-order ordinary differential equations.J Math Anal Appl,1987,127:459-469
[35]Li W G.An application of a global inversion theorem to an existence and uniqueness theorem for a class of nonlinear systems of differential equations.Nonlinear Analysis,2009,70:3730-3737
[36]Yang X.Existence and uniqueness results for periodic solution of nonlinear differential equations.Appl Math Comput,2002,130:213-223
 Acta Mathematica Scientia(English Series)2016年1期
Acta Mathematica Scientia(English Series)2016年1期
- Acta Mathematica Scientia(English Series)的其它文章
- SOME STABILITY RESULTS FOR TIMOSHENKO SYSTEMS WITH COOPERATIVE FRICTIONAL AND INFINITE-MEMORY DAMPINGS IN THE DISPLACEMENT∗
- STABILITY OF VISCOUS SHOCK WAVES FOR THE ONE-DIMENSIONAL COMPRESSIBLE NAVIER-STOKES E QUATIONS WITH DENSITY-DEPENDENT VISCOSITY∗
- STABILITY ANALYSIS OF A COMPUTER VIRUS PROPAGATION MODEL WITH ANTIDOTE IN VULNERABLE SYSTEM∗
- STABILITY OF A PREDATOR-PREY SYSTEM WITH PREY TAXIS IN A GENERAL CLASS OF FUNCTIONAL RESPONSES∗
- NONSMOOTH CRITICAL POINT THEOREMS AND ITS APPLICATIONS TO QUASILINEAR SCHRÖDINGER EQUATIONS∗
- NORMAL FAMILIES OF MEROMORPHIC FUNCTIONS WITH SHARED VALUES∗
