一类三维分段线性系统的异宿轨的存在性

朱道宇

一类三维分段线性系统的异宿轨的存在性

朱道宇

(贵州民族大学理学院，贵州贵阳550025)

研究一类具有3个参数的连续分段线性微分动力系统的异宿轨的存在性.利用光滑子系统的流建立切换流形上的Poincare映射，并结合Taylor展开等方法，证明系统在一定参数条件下存在简单二维异宿轨.

异宿轨;Poincare映射;平衡点;流形

1 预备知识

近年来，非光滑微分动力系统中的分段线性系统，由于其形式的简单性和所呈现的动力学行为的复杂性，它的分支和混沌动力学研究一直受到学者的关注［1－6］.同宿轨和异宿轨是研究高维微分动力系统的混沌动力学的重要工具之一.文献［7］给出了著名的Shilnikov定理，该定理揭示了三维光滑微分动力系统的同宿轨和异宿轨与混沌现象的紧密联系.文献［8］给出了适用于分段光滑微分动力系统的Shilnikov定理，一个三维的连续分段光滑微分动力系统的平衡点当其特征值满足一定条件时，若系统存在同宿轨或异宿环，则在此同宿轨或异宿环的任一邻域内存在无穷多可数个不稳定周期轨，因而存在混沌.一般地，无论对光滑动力系统还是非光滑动力系统来说，同宿轨或异宿轨的存在性的理论证明都是一项比较困难的工作，到目前为止，严格证明非光滑动力系统存在同宿轨或异宿轨的研究成果相对较少［9－17］.本文考虑一类具有3个参数的三维连续分段线性系统，研究其简单二维异宿轨的存在性.

文献［2］提出一类如下形式的三维连续分段线性系统

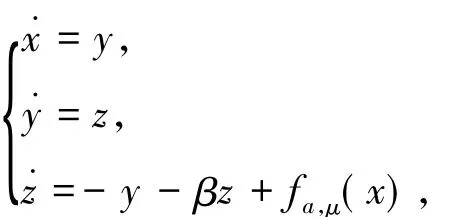
其中，β＞0是耗散项，fa，μ(x)是一个二参数的连续分段线性函数

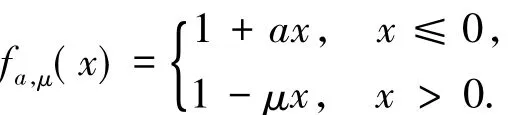
为方便讨论，将上述系统写成矩阵形式

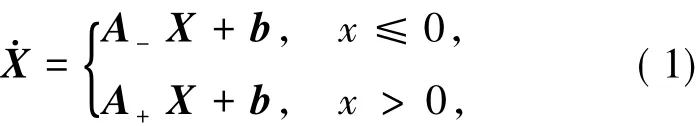
其中向量X=(x，y，z)T，b=(0，0，1)T，系数矩阵

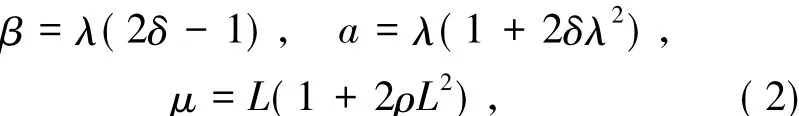
其中

在变换(2)式之下，系数矩阵A－和A+的特征值分别为λ，－δλ±iω和－L，ρL±iΩ，其中i是虚数单位，ω和Ω是正实数，并且

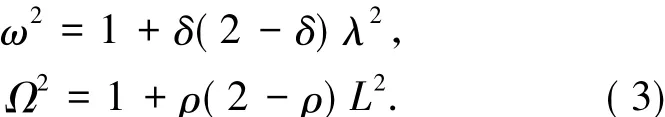
下面选取λ、δ、L为系统(1)的基本参数，并设参数的取值范围是λ，δ，L＞0.由系数矩阵的特征值的形式知平衡点e－和e+都是系统(1)的鞍－焦点.

由矩阵A－的对应于特征值λ的特征向量(1，λ，λ2)T，可算得平衡点e－的一维不稳定流形Wu(e－)在{x≤0}内的部分是半直线I－与切换流形{x=0}相交于点T.由矩阵A－的对应于特征值－δλ+iω的特征向量的实部(1，－δλ，δ2λ2－ω2)T和虚部(0，ω，－2δλω)T，可得平衡点e－的二维稳定流形Ws(e－)在{x≤0}内是半平面

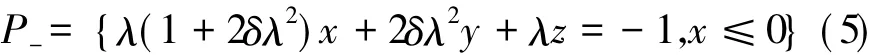
的一部分.P－与切换流形{x=0}相交于直线

要注意的是直线H－只有一部分属于Ws(e－).

由矩阵A+的对应于特征值－L的特征向量(1，－L，L2)T，可得平衡点e+的一维稳定流形Ws(e+)在{x≥0}内的部分是半直线I+与切换流形{x=0}相交于点)T.由矩阵A+的对应于特征值ρL+iΩ的特征向量的实部(1，ρL，ρ2L2－Ω2)T和虚部(0，Ω，2ρLΩ)T，可得平衡点e+的二维不稳定流形Wu(e+)在{x≥0}内是半平面

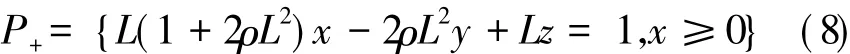
的一部分.P+与切换流形{x=0}相交于直线

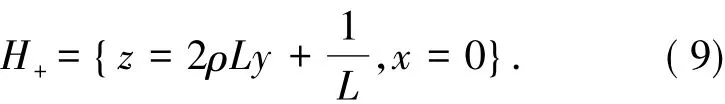
同样，直线H+也只有一部分属于Wu(e+).

2 系统在{x≥0}和{x≤0}内的流

对R3中任意一点p=(xp，yp，zp)T，记过点p的轨线为γp.如果点p在{x≥0}内，令(t)= ((t)(t)，(t))T是系统(1)的满足初值条件(0)=p的解.当(t)≥0时有

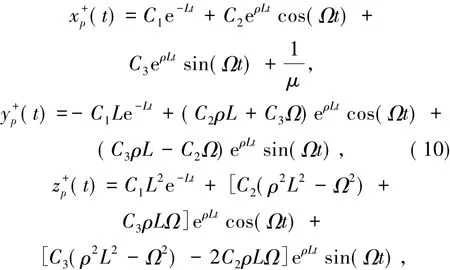
其中

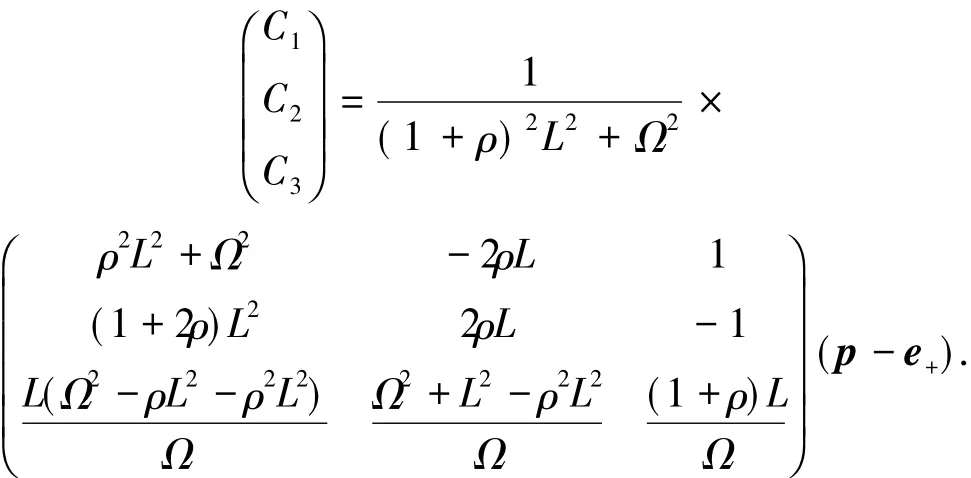
如果xp=0，yp＞0，则由系统(1)的第一个表达式得e＞0，其中e1=(1，0，0)T，表示系统(1)在点p处的向量场.此时轨线γp从区域{x＜0}穿过切换流形{x=0}进入区域{x＞0}.由于系统(1)在{x≥0}内是线性的并且鞍－焦点e+的稳定流形和不稳定流形都与{x=0}相交，如果点p不在e+的稳定流形上，则存在回复时间＞0使得()=0，并且当t∈(0，)时，(t)＞0.简而言之，如果点p满足xp=0且yp＞0，则定义Poincare映射Π+为

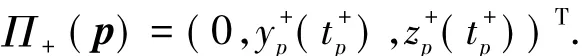
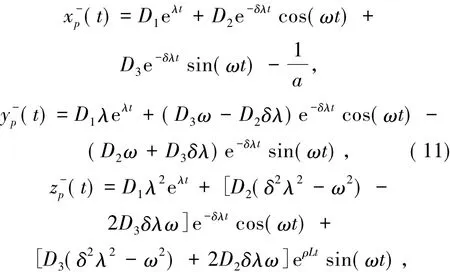
其中

如果xp=0，yp＜0，则e＜0，此时过点p的轨线γp从区域{x＞0}穿过切换流形{x=0}进入区域{x＜0}.由于系统(1)在{x≤0}内是线性的并且鞍－焦点e－的稳定流形和不稳定流形都与{x=0}相交，如果点p不在e－的稳定流形上，则存在回复时间＞0使得()=0，并且当t∈(0，)时，(t)＜0.简言之，如果点p满足xp=0，yp＜0，则定义Poincaré映射Π－为

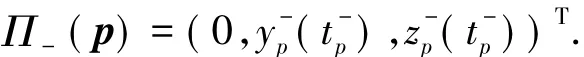
如果点p在z轴上，即xp=yp=0，则e=0，这样的点叫做系统(1)的流与切换流形{x=0}的一个接触点.对于这样的点，设Xp(t)为系统(1)的满足初值条件Xp(0)=p的解.将Xp(t)在t=0处Taylor展开到四阶，并把常数项移到等号左端，得到其第一个分量为

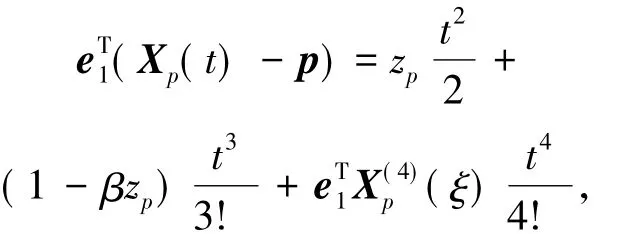
其中ξ的取值介于0和t之间.因此，当zp＜0时轨线γp局部包含在{x≤0}内，当zp＞0时轨线γp局部包含在{x≥0}内，当zp=0时轨线γp从{x＜0}穿过切换流形{x=0}进入{x＞0}.

3 引理和主要结果

系统(1)的简单二维异宿轨是指一条连接平衡点e+和平衡点e－的轨线ρ±⊂Wu(e+)∩Ws(e－)且ρ±与切换流形{x=0}有且只有一个交点.事实上，点就是直线H－与H+的交点，即

考虑半平面P－和P+分别与z轴的交点q－=(0，0，－1/λ)T和q+=(0，0，1/L)T，显然q－和q+都是系统(1)的流与切换流形的接触点.令S－⊂H－是以q－和(q－)为端点的线段，其中是Poincaré映射Π－的逆映射，则与直线H－相交的轨线沿着平衡点e－的稳定流形Ws(e－)进入e－的充分必要条件是交点q－在线段S－上.令S+⊂H+是以q+和Π+(q+)为端点的线段，则与直线H+相交的轨线沿着平衡点e+的不稳定流形Wu(e+)按负向时间进入e+的充分必要条件是交点q－在线段S+上.

证明因为点q+=(0，0，1/L)T在z轴上且z坐标分量大于0，由第2节的分析知轨线γq+局部包含在{x≥0}内.由(10)式得系统(1)的满足初值条件X(0)=q+的解为

q+

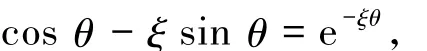
此方程在(π，2π)内有唯一的零点θ0.因此，轨线从点q+到Π+(q+)的回复时间满足Ωt∈(π，2π).将(3)式中Ω的表达式关于变量L作Taylor展开得

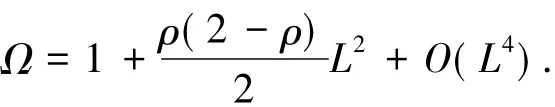
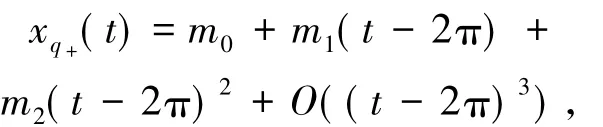
其中

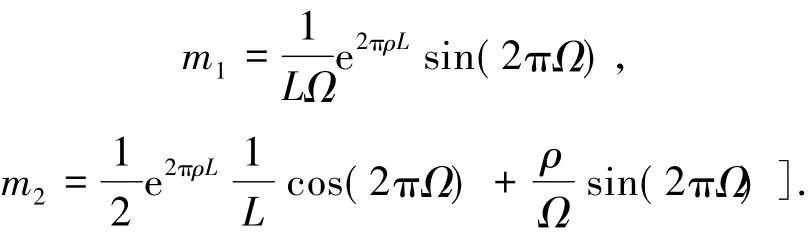
求解关于未知数t的方程

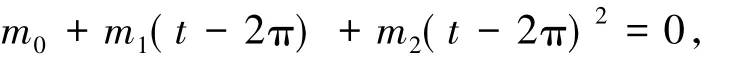
将此近似值带入(13)式的第一式，可算得

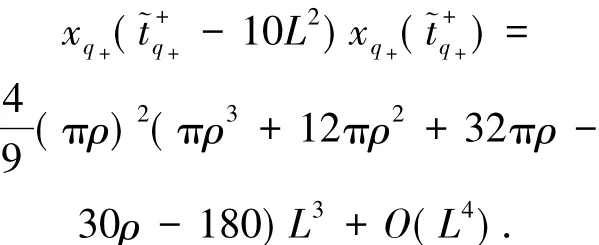
容易验证当0＜ρ＜1.2时，因式πρ3+12πρ2+32πρ－ 30ρ－180＜0，即当且充分小时，10L2)与xq+()异号，于是由零点存在定理有

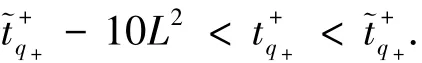
由此得

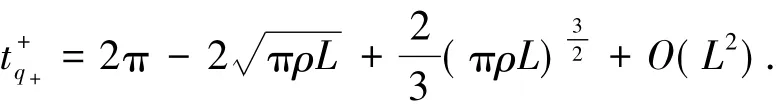
下面计算Π+(q+)的y坐标分量.由(13)式的第二式得

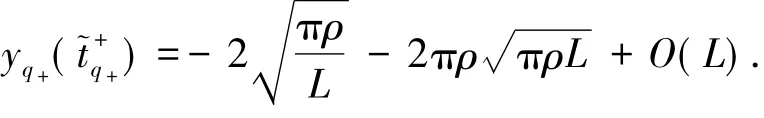
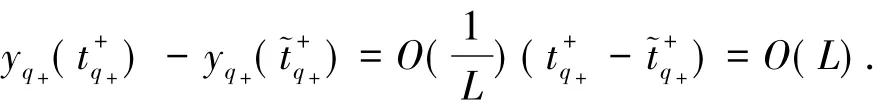
移项得

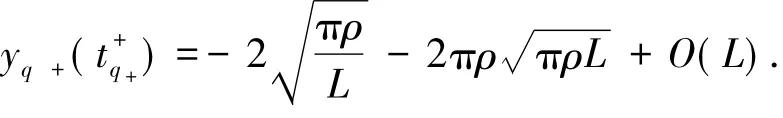
利用与引理1类似的推导方法，可得:

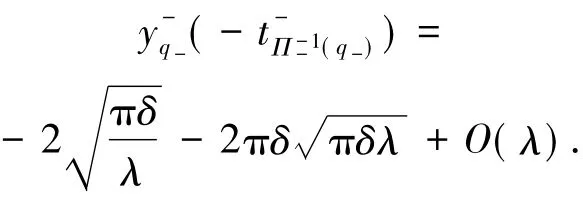
定理1设λ＞0且充分小，0＜δ＜1.3，则当且充分小时，系统(1)有一条二维异宿轨，该异宿轨与切换流形{x=0}有且只有一个交点.

证明由本节一开始的讨论知，只需证明在定理的条件下，直线H－与H+的交点q－∈S+且q－∈S－.由于，而点q+的y坐标分量等于0，因此如果Π+(q+)的y坐标分量小于，则∈S+.由条件(14)式知L＞，所以当λ＞0且充分小时，由引理1得Π+(q+)的y坐标分量为+O(L).又由条件(14)式知+2λδ－λ，所以

由此知点Π+(q+)的y坐标分量满足因而有q－∈S+.同理可证，当λ＞0且充分小，0＜δ＜1.且充分小时，∈S－.定理证完.

此定理说明系统(1)当3个参数满足一定条件时存在一条从平衡点e+到平衡点e－的异宿轨，该异宿轨与切换流形{x=0}有且只有一个交点.根据Shilnikov定理，如果此时还存在一条从平衡点e－到平衡点e+的异宿轨并且参数δ和ρ的取值都在(0，1)区间内，则系统(1)存在混沌.从e－到e+的异宿轨与切换流形{x=0}至少有3个交点，这样的异宿轨的存在性证明对于多参数的分段线性系统来说是困难的，作者将在以后作进一步探讨.

［1］BEMARDOM，BUDD C J，CHAMPNEYS A R，et al.Piecewise－smooth Dynamical Systems:Theory and Application［M］.Appl Math Sci Series，163.Berlin:Springer－Verlag，2008.

［2］AMEODO A，COULLET P，TRESSER C.Possible new strange attractors with spiral structure［J］.Commun Math Phys，1981，79(4):573－579.

［3］ARNEODO A，COULLET P，TRESSER C.Oscillators with chaotic behavior:an illustration of a theorem by Shilnikov［J］.J Stat Phys，1982，27(1):171－182.

［4］SIMPSON D J W，MEISS J D.Andronov－Hopf bifurcations in planar piecewise－smooth continuous flows［J］.Phys Lett，2007，A371(3):213－220.

［5］FREIRE E，PONCE E，RODRIGO F，et al.Bifurcation sets of symmetrical continuous piecewise linear systems with three zones［J］.Internat J Bifur Chaos Appl Sci Engrg，2002，12(8):1675－1702.

［6］CARMONA V，FREIRE E，PONCE E，et al.On simplifying and classifying piecewise linear systems［J］.IEEE Trans Circuits Systems I:Fund Theory Appl，2002，49(5):609－620.

［7］SHILNIKOV L P.A case of the existence of a countable number of periodic motions［J］.Sov Math Dokl，1965，6:163－166.

［8］SILVA C P.Shilnikov theorem－a tutorial［J］.IEEE Trans Circuits Syst，1993，40(10):675－682.

［9］VITALY V，BOGDAN K.Existence of heteroclinic orbits for systems satisfying monotonicity conditions［J］.Nonlinear Anal，2003，55(4):467－491.

［10］MEES A I，CHAPMAN P B.Homoclinic and heteroclinic orbits in the double scroll attractor［J］.IEEE Trans Circuits Syst，1987，34(9):1115－1120.

［11］LI Z，CHEN G R，HALANG W A.Homoclinic and heteroclinic orbits in a modified Lorenz system［J］.Information Science，2004，165(3):235－245.

［12］WILCZAK D.Symmetric heteroclinic connections in the Michelson system:a computer assisted proof［J］.SIAM J Appl Dyn Syst，2005，4(3):489－514.

［13］LLIBRE J，PONCE E，TERUEL A E.Horseshoes near homoclinic orbits for piecewise linear differential systems in R3［J］.Int J Bifur Chaos，2007，17(4):1171－1184.

［14］LI G L，CHEN X Y.Constructing piecewise linear chaotic system based on the heteroclinic Shilnikov theorem［J］.Commun Nonlinear Sci Numer Simul，2009，14(1):194－203.

［15］CARMONA V，FERNANDEZ－SANCHEZ F，GARCIA－MEDINA E，et al.Existence of homoclinic connections in continuous piecewise linear systems［J］.Chaos，2010，20:013124.

［16］李正彪，夏莲.非线性Schrödinger耦合方程组的同宿轨［J］.四川师范大学学报(自然科学版)，2011，34(1):59－62.

［17］李坤琼，刘双，朱长荣.一类新三维混沌系统的脉冲控制和Hopf分支［J］.四川师范大学学报(自然科学版)，2013，36(5):708－711.

Existence of Heteroclinic Orbits for Three-dimensional Piecewise Linear Systems

ZHU Daoyu
(College of Science，Guizhou Minzu University，Guiyang 550025，Guizhou)

The existence of heteroclinic orbits for a three-parametric family of continuous piecewise linear systems is studied.Using Poincare maps established by the flow of smooth subsystems on switch manifold，and combining with Taylor series expansion method，the existence of a simple 2-dimensional heteroclinic orbit under certain parametric conditions is proved.

Heteroclinic orbit;Poincare map;equilibrium;manifold

O193

A

1001－8395(2016)03－0377－05

10.3969/j.issn.1001－8395.2016.03.014

(编辑郑月蓉)

2015－04－03

贵州省科技厅联合基金(黔科合LH字［2014］7377)

朱道宇(1982—)，女，讲师，主要从事微分方程与动力系统的研究，E－mail:daoyu513@163.com

2010 MSC:34C40