利用几何画板探索圆锥曲线试题题根的教学案例
江苏省海门中学证大校区 黄卫平 (邮编:226100)
利用几何画板探索圆锥曲线试题题根的教学案例
江苏省海门中学证大校区黄卫平(邮编:226100)
对于一个试题,削弱其条件,加强其结论,追根溯源得到一个更加普遍性意义的结论,这就是这个试题的题根.如果我们对一个试题疑似它有一个有价值的题根,就应该大胆进行猜测,探索论证其正确性.研究试题的题根,对教师而言,能够有效提升业务素质,对命制试卷具有题库作用;对学生而言,培养研究探索精神和推理论证能力大有益处.在圆锥曲线问题中,利用几何画板研究问题的一般性,探索结论的正确性具有特殊的优势.
下面以一道2015年江苏高考学科基地秘卷(数学第十套)(江苏人民出版社)上的试题为例,和大家分享利用几何画板探索圆锥曲线试题题根的教学案例.
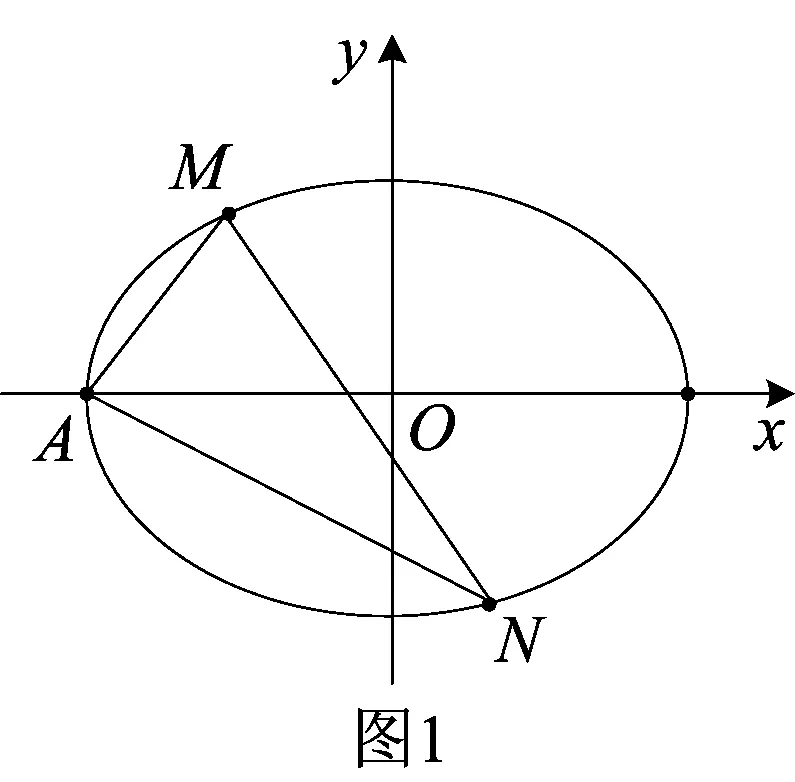
(1)求该椭圆的方程;
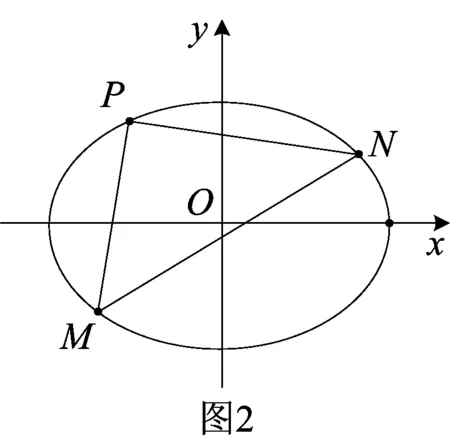
(2)求证:直线MN恒过x轴上的一个定点.
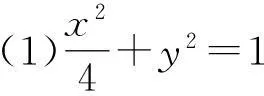
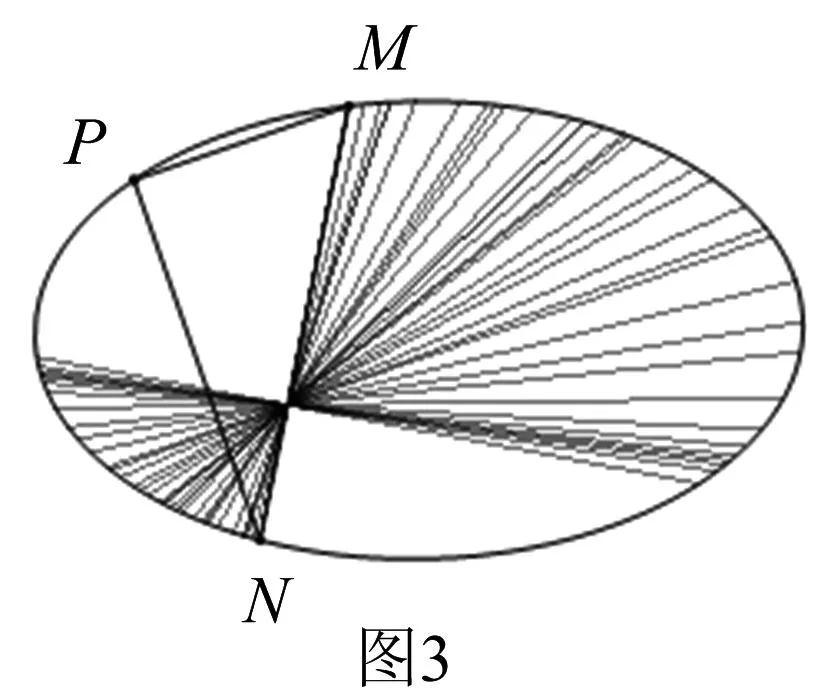
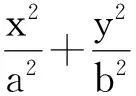
通过几何画板演示发现(如图3),结论是肯定的,下面进行证明.
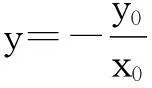
①
②
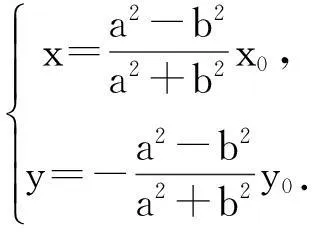
下面证明,当PM、PN斜率都存在时,直线MN也经过点Q.
设直线PM的方程为y-y0=k(x-x0),与椭圆方程联立,消去y,整理得
(b2+a2k2)x2+2a2k(y0-kx0)x+a2(y0-kx0)2-a2b2=0,由韦达定理可知,
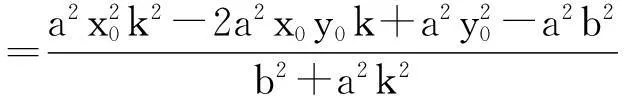
所以yM=kxM+(y0-kx0)
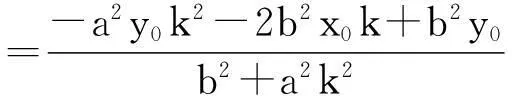
将上述繁分式进行化简,并将分子分母分别按k进行降幂排列,得到
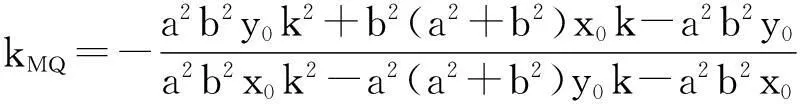
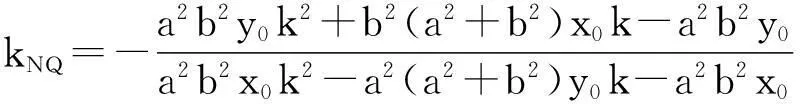
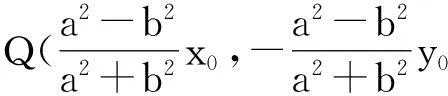
探索2当点P在椭圆上运动的时候,这个定点Q的轨迹有什么特征?
设点Q的坐标为(x,y),则
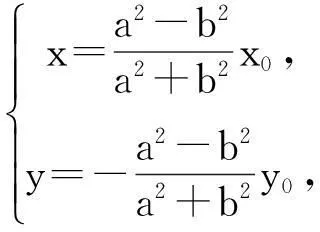
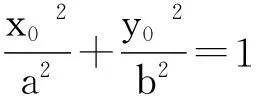
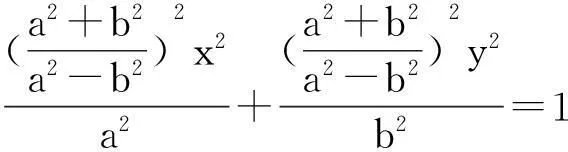
这就是点Q的轨迹方程,轨迹为椭圆,而且这个椭圆和已知椭圆以原点为中心位似.
探索3如果将条件中的“垂直”改为“其它角度”,结论又会如何?
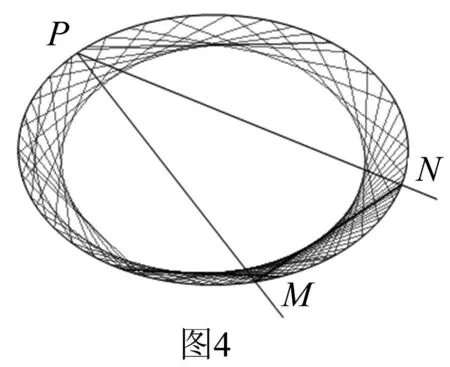
我们以直线PM、PN相交成30°为例,通过几何画板演示发现,直线MN没有过一个定点,但是得到一个有趣的结论:直线MN形成一个包络,这个包络是椭圆(如图4).这个结论利用微分几何知识可以证明,在此就不证明了.
我们将上面的探索结果系统整理成以下结论:
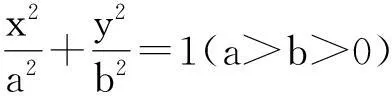
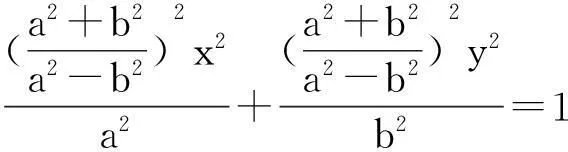
且这个椭圆和已知椭圆以原点为中心位似.
(2)当直线PM与PN不垂直时,直线MN不过定点,但是直线MN形成一个椭圆包络.
探索4对于双曲线是否具有类似结论?
由双曲线方程的特点可知,将结论1中的b2改为-b2就可以得到如下结论:
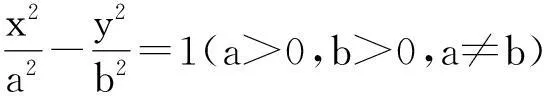
(2)当直线PM与PN不垂直时,直线MN不过定点,但是直线MN形成一个双曲线包络.
探索5对于抛物线是否也有上述类似的结论呢?
通过几何画板演示发现,抛物线也有上述类似的结论.
结论3设P(x0,y0)是抛物线y2=2px(p>0)上的任意一点,过P作两条直线PM、PN交椭圆于M、N两点.
(1)当PM⊥PN时,直线MN恒过一个定点Q(x0+2p,-y0),若点P在抛物线上运动,则这个定点Q的轨迹为抛物线y2=2p(x-2p)(p>0),且这个抛物线是已知抛物线向右平移2p个单位所得.
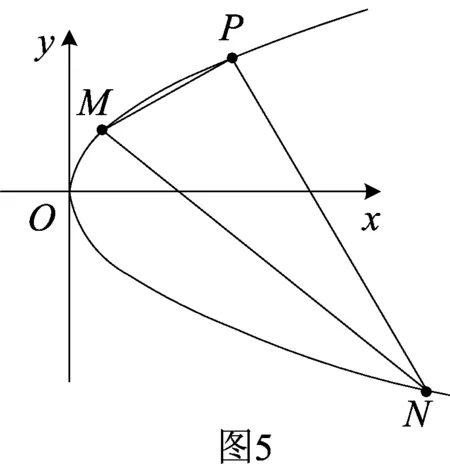
(2)当直线PM与PN不垂直时,直线MN不过定点,但是直线MN形成一个抛物线包络.
证明如图5,设点M(x1,y1),N(x2,y2),
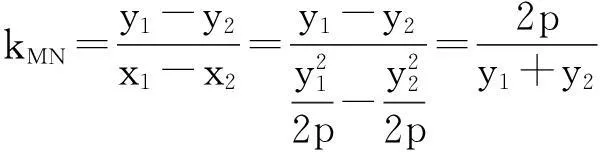
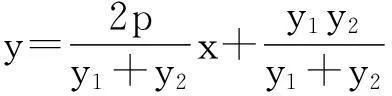
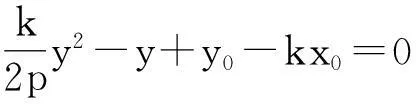
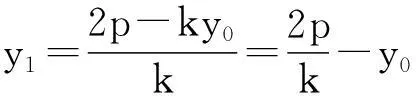
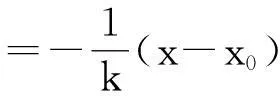
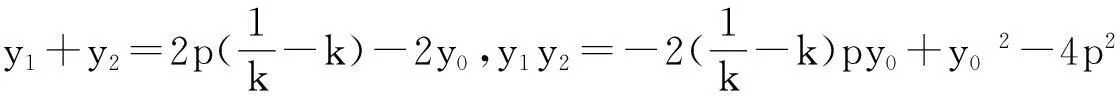
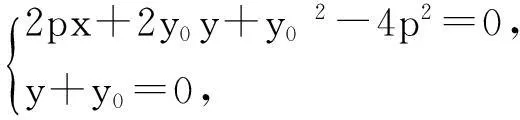
所以直线MN恒过定点Q(x0+2p,-y0).
当点P在抛物线上运动,这个定点Q点轨迹为抛物线y2=2p(x-2p)(p>0),且这个抛物线是已知抛物线向右平移2p个单位所得.
(2)这个结论利用微分几何知识可以证明,在此就不证明了.
以上的探索过程层层深入,将原试题对特殊曲线、特殊位置的结论推广到一般圆锥曲线、一般位置的结论,得到了具有更加广泛意义的题根.现代信息技术、几何画板的使用,使图形的变化更为直观,给探索问题提供方便,使课堂注入了新的活力,学生对这样的课堂很有兴趣,参与探索和研究的积极性很高,而且对椭圆和抛物线问题的证明,分别采取了不同的合理方法.这样的课堂应该多加尝试、研究.
(收稿日期:2016-03-12)

