平面截圆锥(圆柱)的截口曲线
——对2015年浙江高考数学文科第7题的探究

浙江省嘉兴市第一中学　(314500)

吴旻玲　沈新权



平面截圆锥(圆柱)的截口曲线
——对2015年浙江高考数学文科第7题的探究

浙江省嘉兴市第一中学(314500)

吴旻玲沈新权

一、试题呈现

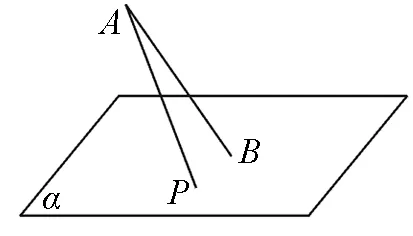
图1

如图1，斜线段AB与平面α所成的角为60°，B为斜足，平面α上的动点P满足∠PAB=30°，则点P的轨迹是( ).

A．直线B．抛物线

C．椭圆D．双曲线的一支

二、试题解析

此题是2015年浙江省高考数学文科的第7题，主要考查圆锥曲线的定义，考查学生的空间想象能力．第一眼看到此题，感觉似曾相识，因为类似的问题曾在2008年浙江省高考数学理科试卷中出现过(见文后的试题链接)，但仔细思考以后我们就发现它们又是有差别的，2008年的试题考查的是用一个与圆柱的轴不垂直的平面去截圆柱所得的截口曲线的轨迹，而这个问题中的AP是以AB为轴的圆锥的母线，且母线与圆锥的轴的夹角为30°，要求的则是用一个平面α(直线AB与平面α所成的角为60°)去截此圆锥所得的截口曲线的轨迹．命题看似俗套却又不乏新颖，而且试题的命题背景源于教材．人教A版选修2-1第二章《圆锥曲线》的章头引言里有这样一句话：“用一个不垂直于圆锥的轴和平面截圆锥，当截面与圆锥的夹角不同时，可以得到不同的截口曲线，它们分别是椭圆、双曲线、抛物线．”因此，此题的答案可能是椭圆，也可能是双曲线、抛物线，对大多数考生来讲，它是一道“熟悉的陌生题”，是一道既能够考查学生用几何知识求点的轨迹的能力的试题，也能够考查学生用代数(向量)方法来求解点的轨迹的能力的试题，因此，作为高考试题来讲，它是一道不可多得的好题目，但对不少考生来说，它则是一道具有一定挑战性的题目．

三、试题解法

方法一：由于试题是选择题，而且答案唯一，所以我们可以用排除法来找到答案．

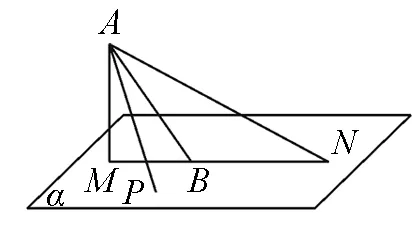
图2

如图2，若记点A在平面α内的射影为M，则∠MAB=30°，所以点M在所求轨迹上，延长MB至N，使AB=BN，则∠NAB=30°，因此点N在所求轨迹上，在运动过程中，点P将从点M运动到点N，且必为封闭图形．因此，排除选项A、B、D，答案为C．

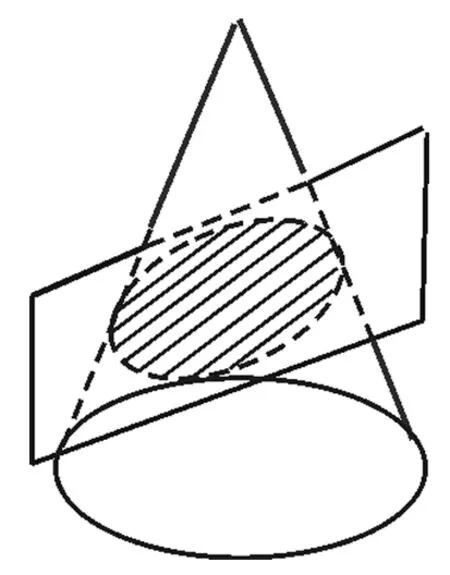
图3

方法二：易知，点P在以AB为轴的圆锥上，该圆锥的母线与轴成30°．因为点P在平面α内，因此P的轨迹是平面α截该圆锥所得截口曲线．因为平面α与轴成60°，根据直观的感觉，我们知道这个曲线是椭圆(如图3)，原因是什么呢?下面我们先用坐标法来证明截口曲线为椭圆．

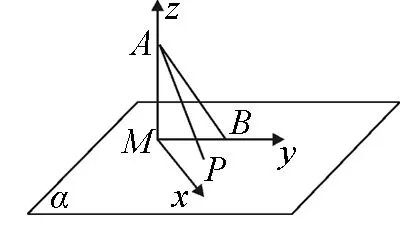
图4

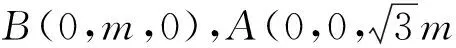
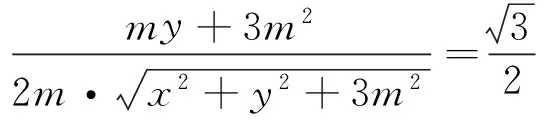
四、试题推广

1.问题提出

若把试题中的斜线段AB与平面α所成的角以及圆锥的母线与轴所成的角一般化，那么结果又会怎么样？即若设斜线段AB与平面α所成的角为θ(0°≤θ≤90°)，∠PAB=φ(0°<φ<90°)，则点P的轨迹是什么？

2.坐标法求解

分析：(1)若线段AB与平面α垂直(θ=90°)，也即用一个与底面平行的平面去截一个圆锥，显然，所得截口曲线为圆．

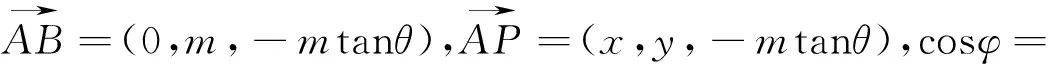
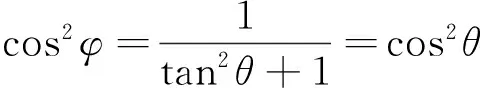
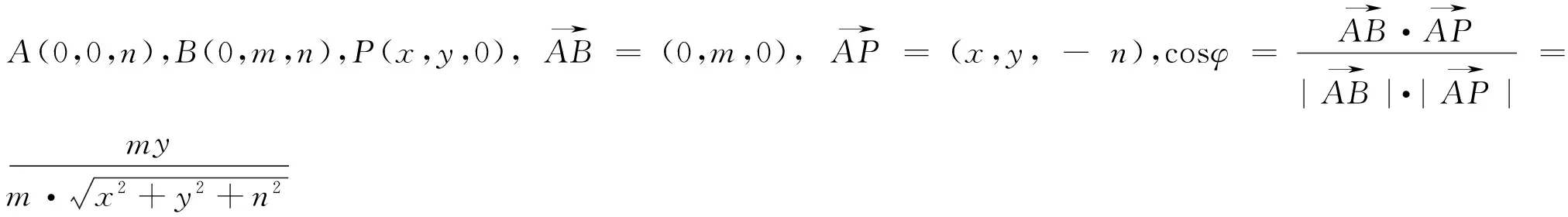
3.一般结论

我们把平面截圆锥问题先降维到二维空间，可得到直线截三角形(如图5)的一般结论：

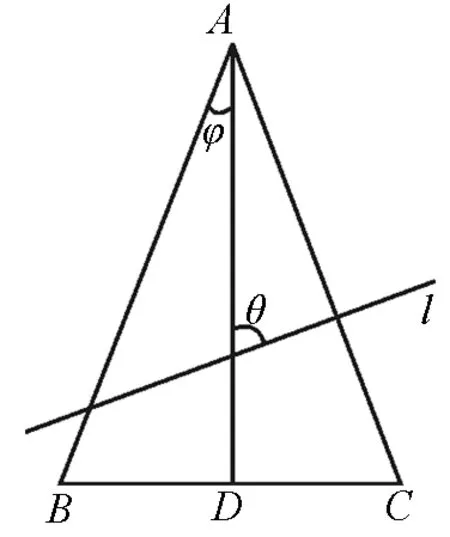
图5

结论1在平面中，AD是等腰ΔABC底边上的高，∠BAD=θ，直线l与AD的夹角为φ，则(1)θ>φ时，直线l与AB(或AB延长线)、AC均相交；(2)θ=φ时，直线l与AB不相交；(3)θ<φ时，直线l与BA的延长线、AC均相交．

类似地，若将等腰三角形拓广为圆锥、直线拓广为平面，那么在三维空间中，结合前面的分析，可得到：

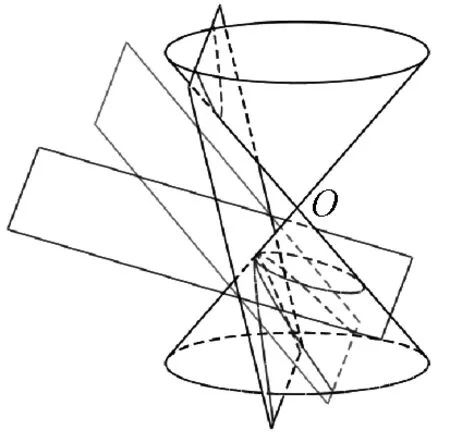
图6

结论2在空间中，直线l与l′相交于O点，其夹角为φ，直线l′围绕直线l旋转得到以O为顶点、l′为母线的圆锥面，平面α(不过圆锥的顶点)与轴l所成角记为θ(0°≤θ≤90°)，则(1)若θ=90°，平面α与圆锥的交线为圆；(2)若θ<90°，①θ>φ时，交线为椭圆；②θ=φ时，交线为抛物线；③θ<φ时，交线为双曲线．如图6所示．

4.几何证明

对于结论2，上文已用坐标法给出了证明，下面我们将从几何定义出发来证明．

我们把两个球嵌入圆锥的内部，分别位于平面α的上、下方，并且与平面α及圆锥都相切(这两个球也称为Dandelin双球)．这里仅证明椭圆和双曲线的情况．

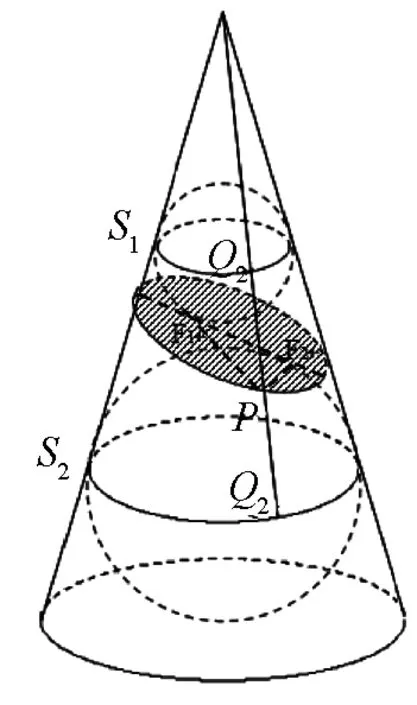
图7

当θ>φ时，设两个球与平面α的切点分别为F1,F2，与圆锥相切于圆S1,S2．在截口的曲线上任取一点P，连接PF1、PF2，如图7所示．过点P作母线分别交圆S1,S2于点Q1,Q2，于是PF1,PQ1是从P出发的两条切线，因此PF1=PQ1，同理，PF2=PQ2．所以，PF1+PF2=PQ1+PQ2=Q1Q2(定值)．因此，截口的曲线是以F1,F2为焦点的椭圆．

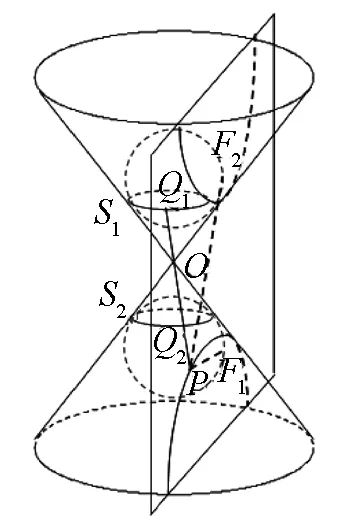
图8

当θ<φ时，平面α与圆锥的上下两个部分都相交，如图8所示．此时，在圆锥上下部分切入Dandelin球，则|PF1-PF2|=|PQ1-PQ2|=Q1Q2(定值)．因此，截口的曲线是以F1,F2为焦点的双曲线．

5.焦点-准线的定义证明

比利时数学家G.F.Dandelin还用这个模型证明了圆锥曲线几何定义与焦点-准线定义的等价性，下面我们介绍焦点-准线的定义证明．

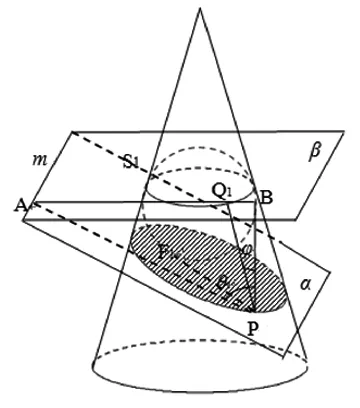
图9

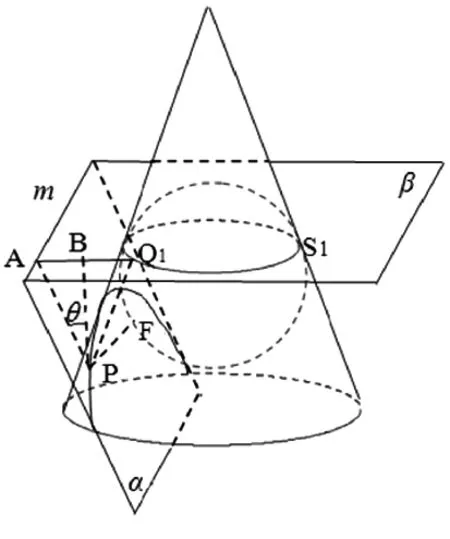
图10

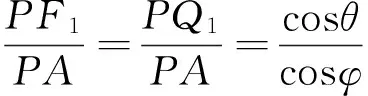
若取曲线上任意一点P，则∠APB=θ，∠Q1PB=φ，因此∠APB=∠Q1PB，所以PA=PQ1，又PQ1=PF，所以PA=PF．即点P到直线m的

距离PA与它到点F的距离相等，因此点P的轨迹是一条抛物线．

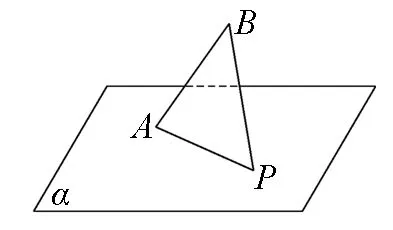
图11

五、试题链接

(2008年浙江高考卷理科第10题)如图11，AB是平面α的斜线段，A为斜足，若点P在平面α内运动，使得ΔABP的面积为定值，则动点P的轨迹是().

A．圆B．椭圆

C．一条直线D．两条平行线

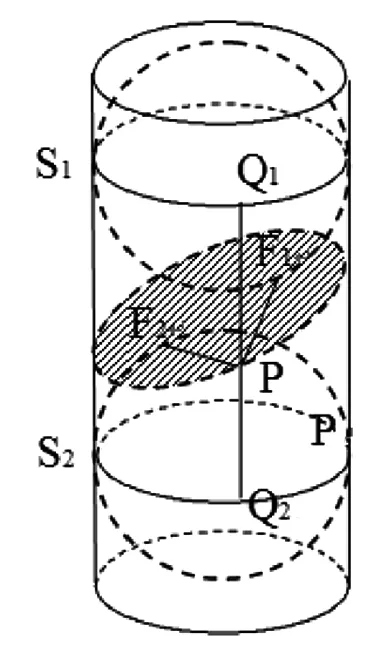
图12

分析：若ΔABP的面积为定值，由于线段AB的长度固定，因此点P到直线AB的距离为定值，即点P在以AB为轴的一个圆柱面上．所以，本题的本质在于讨论用一个平面截圆柱面，截口是什么曲线．我们知道，拿一个平面去截圆柱，若平面与圆柱的轴垂直，则截口曲线为圆；若平面与轴平行，截口曲线为矩形；若平面与轴既不平行也不垂直，则截口曲线为椭圆．因此答案为B．

下面，我们也用前文提到的双球模型来证明截口为椭圆的情况．

设平面α是与圆柱的轴既不平行也不垂直的一个平面，它与圆柱侧面相交．在圆柱中放入两个小球，使它们分别与圆柱侧面、底面和平面α都相切，如图12所示．记上下两个小球与平面α的切点分别为F1、F2，与圆柱面的交线分别为圆S1、S2．在截口曲线上任取一点P，过点P作与轴平行的直线分别与圆S1、S2交于点Q1、Q2．则有PF1+PF2=PQ1+PQ2=Q1Q2(定值)，因此点P的轨迹是以F1、F2为焦点的椭圆．

[1]金卫国．”切香肠”与”Dandelin双球”[J] ．高中数学教与学．2011(5).

[2]周之夫．圆锥截线特征的新证[J] ．数学通报．1998(1).

[3]项武义．圆锥截线的故事[J] ．中学数学月刊．2004(4).

[4]陈丽萍．平面截圆柱生成截口曲线为椭圆的相关问题[J] ．课程教育研究．2015(3).