SOLVABILITY FOR FRACTIONAL FUNCTIONAL DIFFERENTIAL EQUATION BOUNDARY VALUE PROBLEMS AT RESONANCE∗†

Xiangkui Zhao，Fengjiao An，Shasha Guo

（School of Math.and Physics，University of Science and Technology Beijing，Beijing 100083，PR China）



SOLVABILITY FOR FRACTIONAL FUNCTIONAL DIFFERENTIAL EQUATION BOUNDARY VALUE PROBLEMS AT RESONANCE∗†

Xiangkui Zhao‡，Fengjiao An，Shasha Guo

（School of Math.and Physics，University of Science and Technology Beijing，Beijing 100083，PR China）

Abstract

The paper deals a fractional functional boundary value problems with integral boundary conditions.Besed on the coincidence degree theory，some existence criteria of solutions at resonance are established.

fractional boundary value problem；at resonance；coincidence degree theory；integral boundary conditions

2000 Mathematics Subject Classification 30E25

1　Introduction

This paper deals the following fractional functional differential equation boundary value problems at resonance

Fractional derivative was introduced by Leibnitz in the email to L'Hospital［1］. It was not developed before the 20th century，since it was short of a physical meaning or application.In recent decades，the researchers have found that the fractionalderivative has long-term memory and self-similarity so that it can be used in electromagnetic，viscoelasticity，and other fields［2-4］.Motivated by the widely application of fractional derivative，the fractional differential equations have received a lot of attention.There are a lot of papers dealing with the solutions for fractional differential equation boundary value problems［5-13］.

Zhang，Lin and Sun［13］considered the following boundary value problem

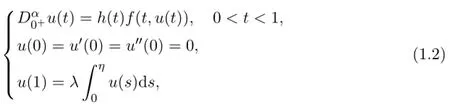
has a nontrivial solution u（t）=ctα-1，c∈R.Hence the research method of［13］is not applicable to（1.1）at resonance.Inspired by the above works，we consider（1.1）at resonance in this paper.

2　Preliminary

Some definitions and lemmas are presented which are available in the proof of our main results.

Definition 2.1 The Riemann-Liouville fractional integral of order α for function f is defined as

provided that the right side is point-wise defined on（0，∞）.

Definition 2.2 The Riemann-Liouville fractional derivative of order α＞0 for function f is defined as

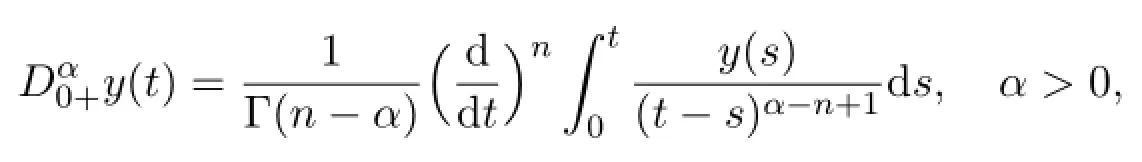
where n=［α］+1，provided that the right side is point-wise defined on（0，∞）.

Lemma 2.1［8］Let α＞0 and assume that u∈C（0，1）∩L（0，1），then the fractional differential equation

Lemma 2.2[8]Assume that u∈C（0，1）∩L（0，1）with a fractional derivative of order α＞0 that belongs to u∈C（0，1）∩L（0，1），then

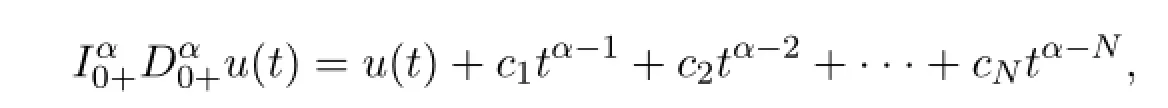
for some ci∈R，i=1，2，···，N.

Definition 2.3We say that the function f：［0，1］×R→ R satisfies L1-Carath´eodory conditions，if

（1）for each u∈R，t■→f（t，u）is Lebesgue measurable on［0，1］；

（2）for almost everywhere t∈［0，1］，u■→f（t，u）is continuous on R；

（3）for each r＞0，there exists a φr∈L1［0，1］satisfying φr（t）＞0 on［0，1］such that＜r implies|f（t，u）|≤φr（t），almost everywhere t∈［0，1］.

We present the following theorem due to J.Mawhin［14］to obtain the existence results.

Theorem 2.1Let X，Y be two Banach spaces，P：X → X，Q：Y→ Y be continuous projectors with ImP=KerL，KerQ=ImL，X=KerL⊕KerP，Y=ImL⊕ImQ，L：domL⊂X → Y be a Fredholm operator of index zero，L|domL∩KerP：domL∩KerP→ImL is invertible，and N：X→Y be L-compact onAssume that the following conditions are satisfied：

（3）deg（JQN|KerL，Ω∩KerL，0）/=0，where J：ImQ→KerL is any isomorphism. Then the equation Lx=Nx has at least one solution in domL∩

In the paper，we use the space X=C（［0，1］）with the normand the space Y=L1［0，1］with the normFor each x∈X，we extend x（t）to

Define a linear operator L：domLwith

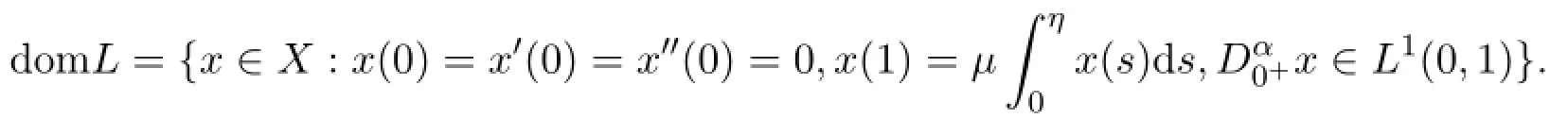
We get that

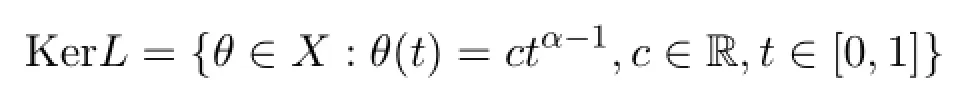
by direct calculations.By the definition of L，we have if y∈Im L，there exists an x∈domL such that y=Lx=Hence

Hence y satisfies

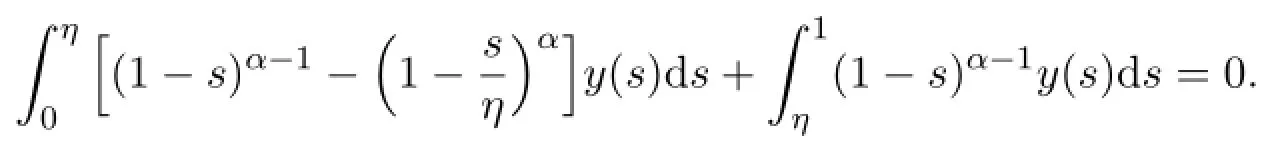
That is

with

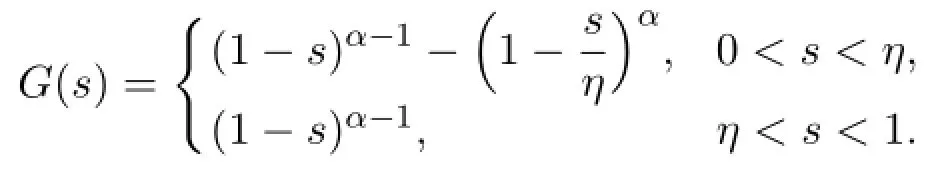
Therefore

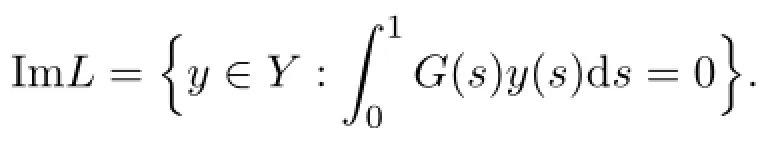
For any y∈Y，let y1=y-Qy，then

Hence y1∈KerQ，that is Y=KerQ+ImQ.If Qy=0，then y∈ImL.Therefore ImL=KerQ and Y=ImL+ImQ.Let y∈ImL∩ImQ and assume that y= c/=0，since y∈ImQ.We get c=0 from∫10G（s）ds/=0，since y∈ImL.Hence Y=ImL⊕ImQ，that is dimKerL=codimImL=1.Therefore L is a Fredholm operator of index zero.

Define a continuous projection P：X→KerL as

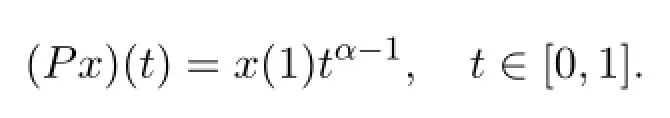
It is easy to get P2x=Px，ImP=KerL.Hence X=KerL⊕KerP.Therefore，there is a unique decomposition x（t）=ρtα-1+x1（t）such that ρ∈R and x1∈KerP for every x∈X.Let LP：domL∩KerP→ImL be the restriction of L on domL∩KerP，then LPis invertible.Set KP=L-1P，then

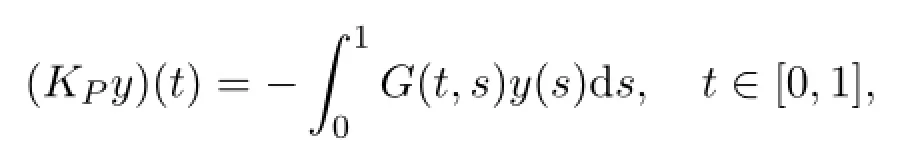
for any y∈ImL with

In fact，it is clear that LKPy=y for y∈ImL.By the definition of domL and KP，we have，if x∈domL∩KerP，then x（0）=x′（0）=x′（0）=x（1）=0，hence

Let a nonlinear operator N：X→Y be defined as

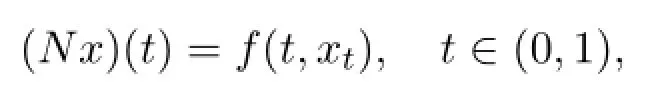
then the boundary value problem（1.1）equals to

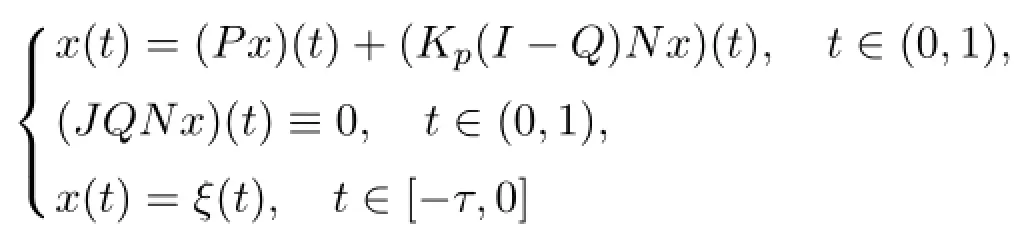
with J：ImQ→KerL being an isomorphism.Next，we illustrate thatis bounded and KP，Qis compact with KP，Q=KP（I-Q）N.That is the map N：X→Y is L-compact on

Lemma 2.3If f：［0，1］×R→R satisfies L-Carath´eodory conditions，then N：X→Y is L-compact onwith Ω⊂X.

3　Existence Results

Theorem 3.1 Assume f：［0，1］×R→R satisfies S-Carath´eodory condition. Assume that：

（H1）There exist two functions p，r∈Y such that for all x∈R，t∈［0，1］

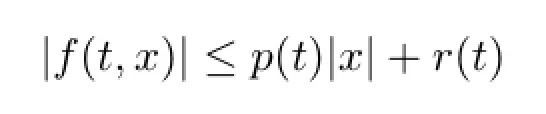
with p，r∈Y，（α+µη）∥p∥Y＜Γ（α+1）；

（H2）there exists a constant M＞0 such that if|x（t）|＞M for all t∈［η-τ，1］then

（H3）for θ∈KerL，there exists a constant M∗＞0 such that if|θ（1）|＞M∗，

is satisfied.

Then the boundary value problem（1.1）has at least one solution in X.

Proof Let X，Y，L，N，P，Q be defined as above.Let

If x∈Ω1，then x∈domLKerL，Nx∈ImL=KerQ.Hence

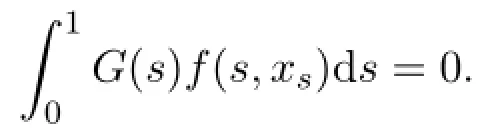
By（H2），there exists a constant t0∈［η-τ，1］such that|x（t0）|≤M.A function x satisfies Lx=λNx if and only if x is a solution of

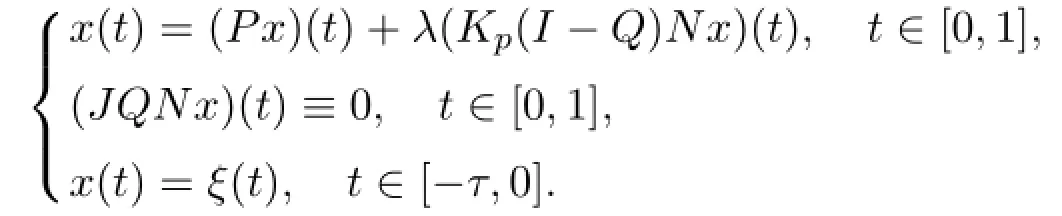
Hence

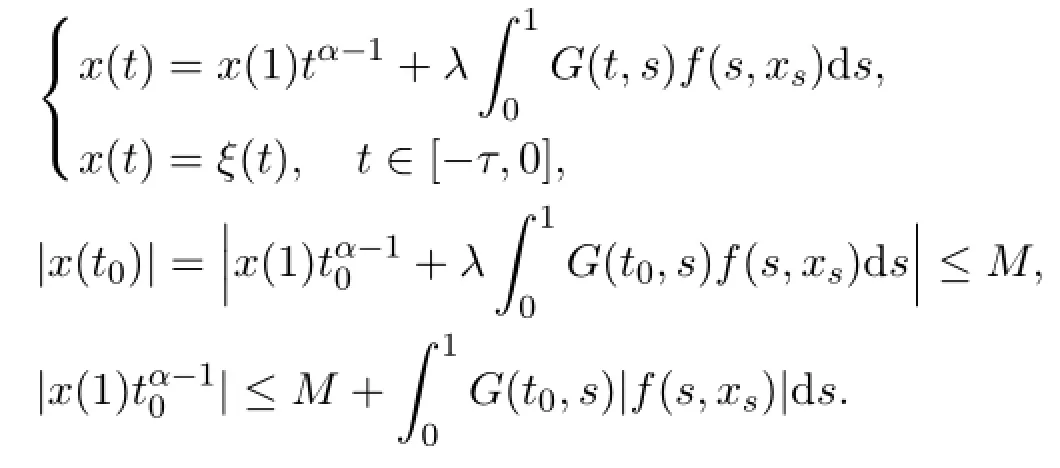
Therefore

Therefore

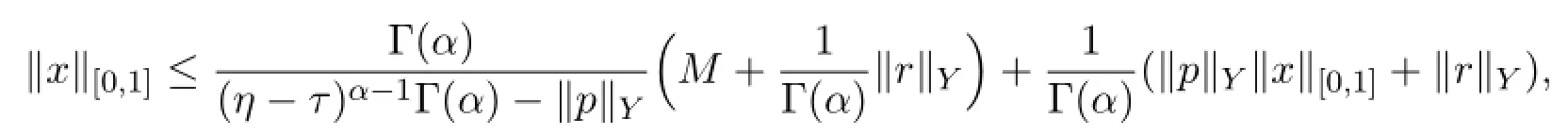
thus Ω1is bounded.

Let

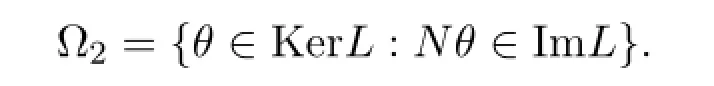
If θ∈Ω2，thenthat is

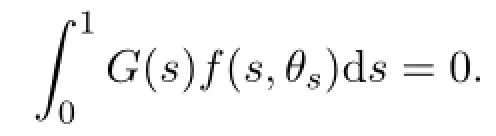
Let

where J：KerL→ImQ is a linear isomorphism given by J（θ（t））=θ（1）.If x∈Ω3and the first part of（H3）holds，then we have

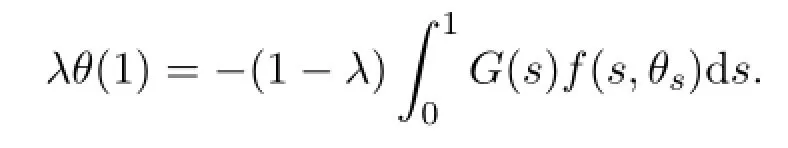
If λ=1，then θ（1）=0，if λ=0，by the first part of（H3），we get that

which is a contradiction，hence，thus Ω3is bounded.

If the second part of（H3）holds，set

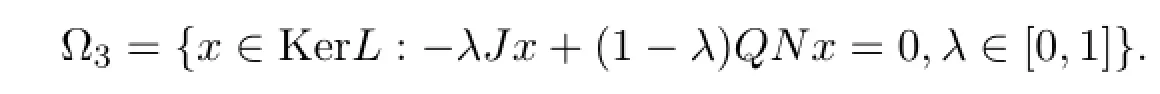
Similarly，we can prove that Ω3is bounded.

Let Ω be a bounded open set of X such thatBy Lemma 2.3， N is L-compact onThen

Finally，we illustrate that（3）of Theorem 2.1 is satisfied.Let

according to the above arguments，we know H（x，λ）0，for all x∈（KerL）∩∂Ω，thus，by the homotopy property of degree

Then by Theorem 2.1，Lx=Nx has at least one solution in（domL）∩Hence problem（1.1）has at least one solution.The proof is complete.

4　Example

Example 4.1 Consider the following boundary value problem

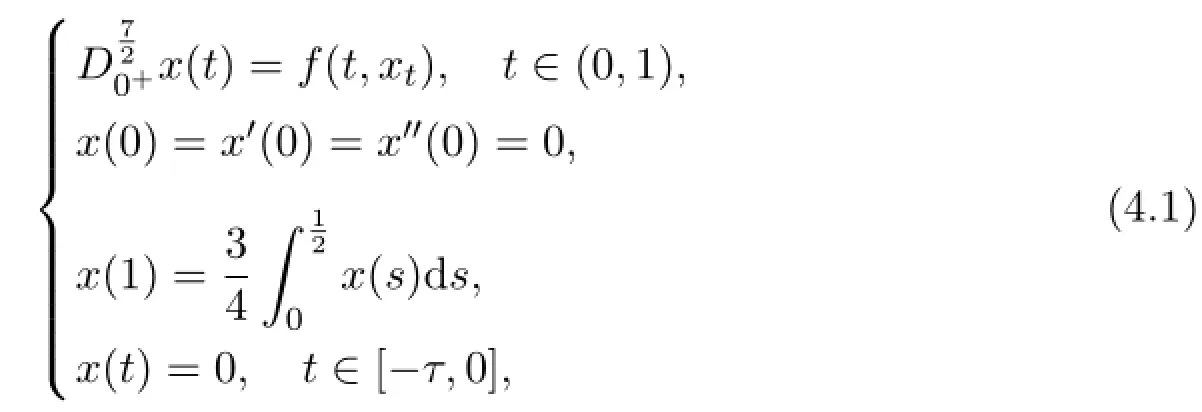
where

Corresponding to problem（1.1），we have thatBy simple calculation，we can get that（H1），（H2）and（H3） hold.By Theorem 2.1，problem（4.1）has at least one solution.

References

［1］G.W.Leibnitz.Letter from hanover，germany，september 30，1695 to g.a.L'hospital. Leibnizen Mathematische Schriften.Olms Verlag，Hildesheim，Germany，1962，First published in 1849.

［2］K.S.Miller，B.Ross，An Introduction to the Fractional Calculus and Fractional Differential Equations，Wiley，New York，1993.

［3］I.Podlubny，Fractional Differential Equations，Academic Press，New York，Londen，1999.

［4］A.A.Kilbas，H.R.Srivastava，J.J.Trujillo，Theory and Applications of Fractional Differential Equations，in：North-Holland Math.Studies，vol.44，Elsevier，2006.

［5］A.Babakhani，V.D.Gejji，Existence of positive solutions of nonlinear fractional differential equations，J.Math.Anal.Appl.，278（2003），434-442.

［6］C.S.Goodrich，Existence of a positive solution to systems of differential equations of fractional order，Comput.Math.Appl.，62（2011），1251-1268.

［7］Y.Zhao，S.Sun，Z.Han，Q.Li，The existence of multiple positive solutions for boundary value problems of nonlinear fractional differential equations，Commun.Nonlinear Sci. Numer.Simulat.，16（2011），2086-2097.

［8］Z.Bai，H.L¨u，Positive solutions for boundary value problem of nonlinear fractional differential equation，J.Math.Anal.Appl.，311（2005），495-505.

［9］W.Jiang，Solvability of fractional differential equations with p-Laplacian at resonance，Appl.Math.Comput.，260（2015），48-56.

［10］Y.Liu，S.Chen，L.Ou，Solvability of Sturm-Liouville boundary value problems for multiple order fractional differential equations，Arab J.Math.Sci.，（2015），doi：10.1016/ j.ajmsc.2015.08.001.

［11］R.P.Agarwal，M.Benchohra，S.Hamani，A survey on existence result for boundary value problems of nonlinear fractional differential equations and inclusions，Acta Appl. Math.，109（2010），973-1033.

［12］S.Marano，D.Motreanu，Infinitely many critical points of non-differentiable functions and applications to a Neumann type problem involving the p-aplacian，J.Differ.Equ.，182（2002），108-120.

［13］X.Zhang，L.Wang，Q.Sun，Existence of positive solutions for a class of nonlinear fractional differential equations with integral boundary conditions and a parameter，Appl.Math.Comput.，226（2014），708-718.

［14］J.Mawhin，Topological degree methods in nonlinear boundary value problems，in：NSFCBMS Regional Conference Series in Mathematics，American Mathematical Society，Providence，RI，1979.

（edited by Mengxin He）

∗Supported by the Fundamental Research Funds for the Central Universities.

†Manuscript received December 16，2015；Revised May 30，2016

‡Corresponding author.E-mail：xiangkuizh@ustb.edu.cn