例谈几类解题方法的妙用
☉西安交通大学苏州附属中学 蒋亚军
例谈几类解题方法的妙用
☉西安交通大学苏州附属中学蒋亚军
高中三年的数学知识多而且杂,解题方法往往要综合和灵活运用函数与方程、转化与化归、数形结合、分类与整合、构造法、分离参数法等各种数学思想方法.虽然某些题有一定的解题模式和套路,但又极具灵活性和综合性,不少题目用常规思路和方法求解,要么过程繁难,要么运算复杂,学生只好“望题兴叹”,因此对不少考生来说,真是“爱恨交加”.笔者结合多年的高三数学专题复习教学,谈谈几种解题方法的运用,不当之处,敬请指正.
一、巧用主元法解题
数学中解答多元问题时,如果把它们不分主次来研究,问题很难解决,所谓“主元”方法就是在一个多元数学问题中以其中一个为“主元”,将问题转化为一元的函数问题,使得在求解最值问题中降低思维难度.
例1已知函数f(x)=3x+a与函数g(x)=3x+2a在区间(b,c)上都有零点,则的最小值为_____.(江苏省泰州市2014届高三上学期期末考试数学试卷14)
分析:本题的目标函数有三个变量,这对学生思维增加了很大的难度,若观察出变量a的最高次数为2,则可将a看成主元将式子变形为二次函数去求解,于是可以收到“避虚就实、变繁成简,化难为易”的解题效果.

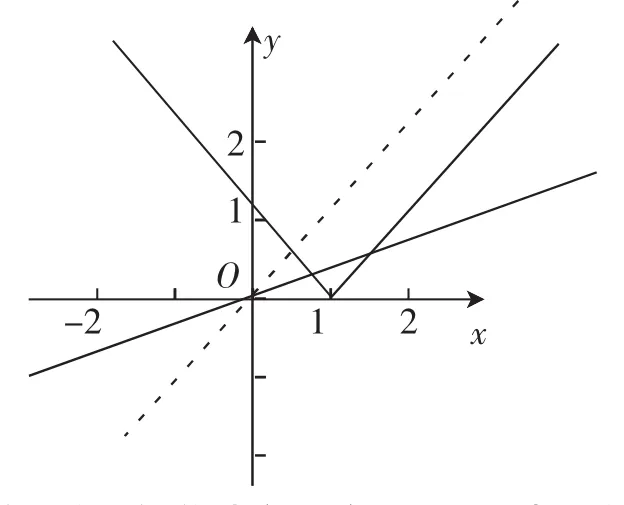
则可得b-c 以上利用主元策略解决了一类“多元”函数最值问题.当我们遇到多元问题时,面对诸多元素,主元策略往往给我们一个头绪,一条主线,化多元问题为一元问题,体现了化归与转化思想.从上述例题中不难看出“主元法”是解题的一种重要的思考方法,我们如能灵活地运用它,就可巧辟捷径,顺利找到合理的解题途径.利用这种思维策略,对于培养学生良好的思维品质,提高研究问题和解决问题的能力大有裨益. 很多学生在解有关函数问题中常出错的原因主要是不善于运用数学中的矛盾转化.善于解决数学问题,就是善于运用数学中的矛盾转化.在解函数问题的中,如果学生能善于用辩证的思维将矛盾转化,并能够举一反三,往往可以很快捷地解决问题. 1.整体与局部的转化 整体与局部是对立统一的.解题有时从整体考虑可以使我们摆脱对独立的局部细节的纠缠,使眼界开阔;而有时从局部入手,各个击破,从而使得整体解决. 例2求函数y=sinx+cosx+sinxcosx的最值. 分析:由于(sinx+cosx)2=1+2sinxcosx,所以可以把sinx+cosx当作一个整体进行换元.令t=sinx+cosx,则1,则容易求出最大值为,最小值为-1. 2.具体与抽象的转化 数是形的高度抽象,而形是数的具体、形象的表达.数与形之间的转化本质上就是具体与抽象之间的转化.华罗庚先生也曾指出“数缺形时少直观,形缺数时难入微”,这充分揭示了两者之间相辅相成、相得益彰的辩证关系. 例3对关于x的两个函数y1=|x-1|和y2=ax(a≠0),若不等式y1≤y2的解集为闭区间[m,n],其中m 分析:对于此绝对值不等式,常规方法是去绝对值,按x≥1和x<1讨论,在每一类中解不等式时又要对a进行讨论,过程极其复杂. 利用数与形之间的转化,即具体与抽象之间的转化,由数形结合思想分别作出函数y=|x-1|和y=ax(a≠0)的图像,如图. 由图像可知,解集为闭区间[m,n],当且仅当0 因此,实数a的取值范围为0 3.已知与未知的转化 已知与未知是相对而言的,解题时可以根据需要把已知当作未知,也可以把未知当作已知. 例4设a∈R,求关于x的函数y=(a2+1)x2+ax-1的零点最大值和最小值. 分析:函数y=(a2+1)x2+ax-1的零点就是一元二次方程(a2+1)x2+ax-1=0的根,此题的常规方法就是用求根公式求出方程的根,然后求最大值和最小值.这种方法看似可行,但实际操作起来很困难. 从辩证的方法考虑,改变思维方向.我们不妨把a视为未知量,x视为已知量,则原方程可以整理为关于a的一元二次方程x2a2+xa+(x2-1)=0.显然x≠0(否则得出-1= 0,矛盾),由a∈R知,Δ=x2-4x2(x2-1)≥0,解得.因此,原方程的最大实根为,最小实根 4.相等与不等的转化 相等与不等是客观世界的一对矛盾,也是数学中的两个重要关系.在解题时,相等的问题可以通过不等关系求解,不等的问题也可以转化为相等关系求解. 例5已知满足函数y=x2+bx+c的函数值为正的x的集合为},求函数y=x2+bx+c的函数值为负的x的集合. 分析:此题直接求解很困难,我们可以考虑相等与不等之间的转化.从辩证的方法考虑,通过分析问题的整体结构,由条件可知,-2和-是关于x的方程x2+bx+c=0的两个根,则由韦达定理可知,进而易求得所求函数y=x2+bx+c的函数值为负的x的集合为 通过对解决函数问题中体现出来的辩证法思想的系统归纳和总结,能够使学生从中学会用联系的、运动变化和发展的观点观察和思考问题.与此同时,由于对辩证法这种科学的思想方法的了解和掌握,又可以反过来指导学生的思想和行动,从而也相应地提高了他们正确地分析函数问题和解决函数问题的能力. 函数压轴题是一个热点,其中一类常见函数问题是证明函数不等式或者根据函数不等式恒成立求参数的范围.这类问题综合性强,思维量大,能力要求高,大部分学生在碰到这类问题时感觉困难,无从下手.而“放缩法”是解决这类问题的有效手段,但在放缩过程中,又会常常出现思维受阻的现象,此时我们不仅需要熟悉一些常见的函数不等式,而且还要掌握一些常见的基本放缩方法,明确放缩点. 1.直接放缩法 (1)求f(x)的单调区间和极值. (2)是否存在实数a,使得关于x的不等式f(x)≥a的解集为(0,+∞)?若存在,求a的取值范围;若不存在,试说明理由. 解:(1)略; 所以当a≤0时,关于x的不等式(fx)≥a的解集为(0,+∞). ②当a>0时,下面先证明不等式:当x≥4时,lnx< 综合①②知,存在a,使得关于x的不等式f(x)≥a的解集是(0,+∞),且a的取值范围是(-∞,0]. 点评:一般先分析函数的特点,看是否具有某些明显的性质.这里先通过观察发现,可对函数变形说明f(x)>0恒成立,然后只要再举例说明对任意大于零的数a,存在x∈(0,+∞)使得f(x) 2.先求导后放缩法 例7设函数f(x)=ex-1-x-ax2. (1)当a=0时,求f(x)的单调区间; (2)若当x≥0时,f(x)≥0,求a的取值范围. 解:(1)略. (2)f′(x)=ex-1-2ax,由(1)知,ex≥1+x,当且仅当x=0时等号成立.所以f′(x)≥x-2ax=(1-2a)x,从而当1-2a≥ 0,即a≤时,f′(x)≥0(x≥0),又f(0)=0,所以当x≥0时,f(x)≥0. 由ex>1+x(x≠0)可得e-x>1-x(x≠0),从而当时,f′(x) 点评:对比较复杂的含有指数,对数的函数表达式,当不能观察出某些明显性质时,可先尝试求导再观察.这里对f(x)求导后,利用不等式ex≥1+x对导函数进行放缩,得到使f(x)≥0成立的一个必要条件,然后再利用不等式e-x>1-x(x≠0)对导函数进行放缩说明当a>时,f(x)≥0不恒成立,从而求出a的取值范围,这里采取的方法是先对函数求导再对导函数进行放缩求解,不妨称之为先求导后放缩方法. 3.先放缩后求导法 碰到证明函数不等式或求函数中的参数取值范围时我们往往会采取先求导后放缩得的方法来处理,但有时候我们反过来采取先对函数进行放缩再来求导会事半功倍. (1)求a,b的值; 证明:(1)易得a=0,b=-1. 所以g(x)在(0,2)内单调递增. 点评:对比较复杂函数求导后发现任很复杂不好处理时可以回过头来再仔细观察能不能先对函数进行化简或放缩.这里如果直接构造函数,求导数,导函数既含有无理式又含有分式比较复杂,所以想到先用不等式把根式去掉,把f(x)放大:f(x)=ln(x+1)+,再把问题转化为证明ln(x+1)+成立,这样使问题迎刃而解.这里用到的方法是先放缩再构造函数求导证明,非常简洁,不妨称之为先放缩后求导法.该问题也可以采取先求导再放缩法,利用ln(x+1)≤x和对导函数进行放缩来判断导函数的符号,进而证明(在此不再赘述). 对函数进行放缩是我们求解有关函数问题的一种常用方法,在采用放缩法时,我们要用扎实的知识和一定的能力,能根据问题的特点以及函数结构,在相关知识的指导下,找准放缩点,找到放缩不等式,这样才能达到避繁就简、化难为易、事半功倍的效果. 以上仅仅列举了三种常见的解题思想,在实际教学实践中远不止这些,只要我们肯观察,常动脑,就会有意想不到的收获.二、利用辩证法解题
三、巧用放缩法解题

